#! https://zhuanlan.zhihu.com/p/656965503
Z变换
引言
Z变换是数字信号处理中将离散时间信号从时域转换到复频域(Z域)的重要数学工具。通过Z变换可以分析离散时间系统的零极点,辅助数字滤波器的设计,可以将常系数的线性差分方程转化为代数方程求解。与连续时域的拉普拉斯变换类似,Z变换构成了离散信号处理理论体系的基础。
Z变换的定义
对于离散时间信号 \(x[n]\),其Z变换定义为:
\({\displaystyle X(z)={\mathcal {Z}}\{x[n]\}=\sum _{n=-\infty }^{\infty }x[n]z^{-n}}\)
从Z变换的定义可以看出Z变换是幂级数,幂级数只有收敛时,Z变换才有意义,因此每一个Z变换都对应一个Z的收敛域(ROC)
Z变换是复变函数,其中自变量Z是一个复数,在这里我们用极坐标的形式来表示,\(z=r^{j\omega}\)
Z变换的收敛域
给定\(x[n]\), 能使\(X(z)\)收敛的所有z值的集合称为\(X(z)\)的收敛域。 根据幂级数收敛的条件,如果满足如下的绝对可和的条件,则Z变换收敛: \(\displaystyle \sum _{n=-\infty }^{\infty }|x[n]z^{-n}|<\infty\)
其中z的取值范围,就称为Z变换的收敛域。
收敛域内不能有极点的存在。极点通常与函数的分母的因子相关联,当分母为零时,就会导致函数在某些点处出现极点。例如,对于有理函数(分子和分母都是多项式的函数),分母的根(使分母等于零的点)通常对应于函数的极点。零点通常与函数的分子的因子相关联,当分子为零时,函数的值为零。对于有理函数,分子的根(使分子等于零的点)通常对应于函数的零点。
例:因果序列\(x[n]=a^{n}u[n]\)的收敛域
我们可以计算这个序列的Z变换,首先使用Z变换的定义:
\(\displaystyle X(z) = \sum_{n=0}^{\infty} x[n]z^{-n} = \sum_{n=0}^{\infty} (a^n u[n])z^{-n}\)
由于 \(u[n]\) 在 \(n < 0\) 时的值为0,我们可以将求和范围限制为 \(n \geq 0\):
\(\displaystyle X(z) = \sum_{n=0}^{\infty} (a^n)z^{-n} = \sum_{n=0}^{\infty} \left(\frac{a}{z}\right)^n\)
上面的级数是一个几何级数,其通项为 \(\left(\frac{a}{z}\right)^n\)。几何级数的和的条件是其公比的绝对值小于1。在这种情况下,公比为 \(\left|\frac{a}{z}\right|\),因此要使级数收敛,需要满足:
\(\displaystyle \left|\frac{a}{z}\right| < 1\)
解这个不等式,我们得到:
\(\displaystyle |z| > |a|\)
这表示因果序列 \(x[n] = a^n u[n]\) 的Z变换 \(X(z)\) 在复平面上的收敛域 \(|z| > |a|\)。
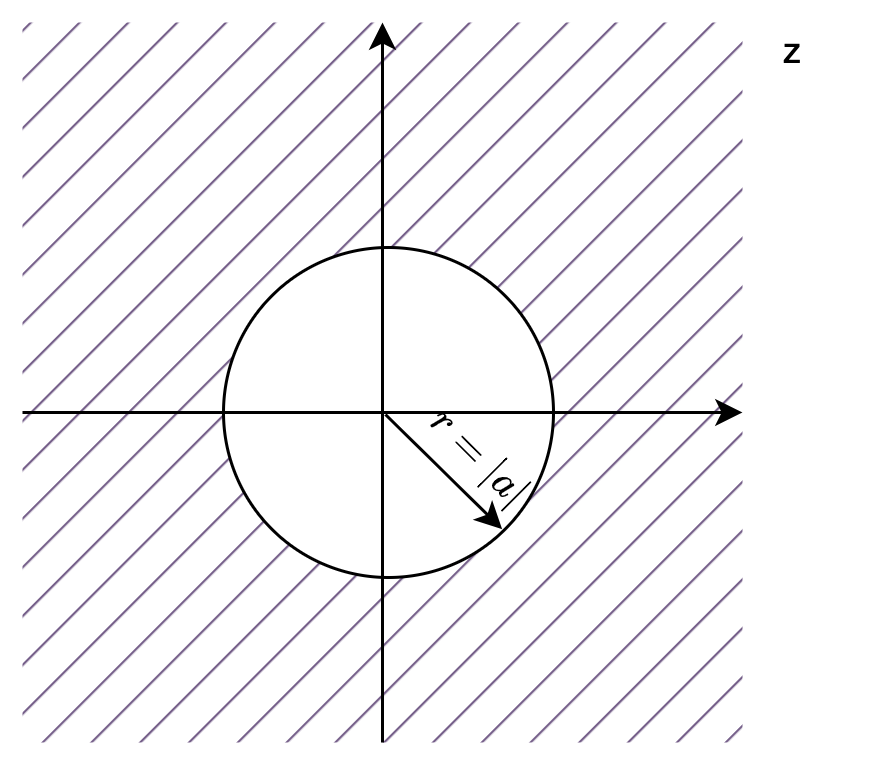
因果序列的收敛域总是大于某个半径,并包括了无穷大的点。可以这么说,如果一个序列在无穷远的地方是收敛的,那么它就是因果的。
例:反因果序列\(x[n]=-a^{n}u[-n-1]\)的收敛域
同样地利用Z变换的定义:
\(\displaystyle X(z) = \sum_{n=-\infty}^{\infty} x[n]z^{-n} = -\sum_{n=-\infty}^{\infty} (a^n u[-n-1])z^{-n}\)
由于 \(u[n]\) 在 \(n \geq 0\)时的值为0,我们可以将求和范围限制为\(n \leq -1\):
\(\displaystyle X(z) = - \sum_{n=-\infty}^{-1} (a^n)z^{-n} = - \sum_{n=1}^{\infty} \left(\frac{z}{a}\right)^n = 1- \sum_{n=0}^{\infty} \left(\frac{z}{a}\right)^n\)
上面的级数是一个几何级数,其通项为 \(\left(\frac{z}{a}\right)^n\)。几何级数的和的条件是其公比的绝对值小于1。在这种情况下,公比为 \(\left|\frac{z}{a}\right|\),因此要使级数收敛,需要满足:
\(\displaystyle \left|\frac{z}{a}\right| < 1\)
解这个不等式,我们得到:
\(\displaystyle |z| < |a|\)
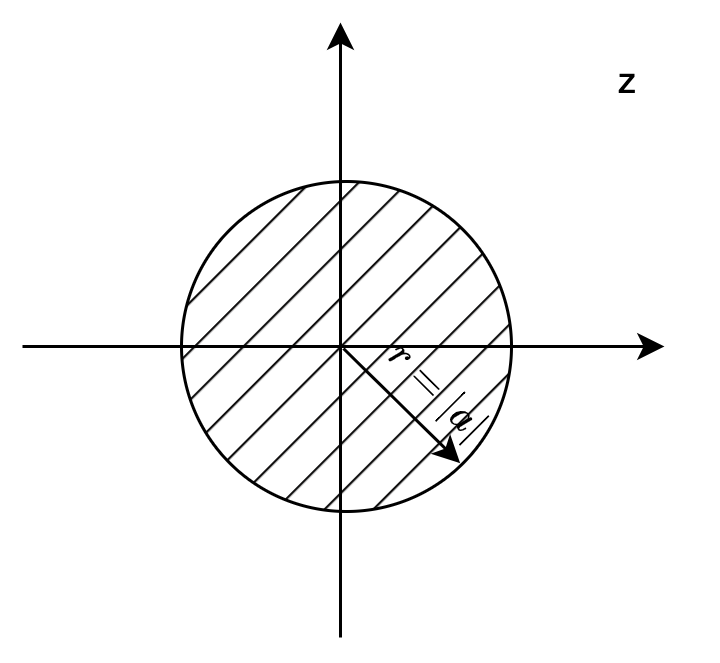
反因果序列的收敛域总是小于某个半径,并包括了零点。可以这么说,如果一个序列在零点的地方是收敛的,那么它就是反因果的。
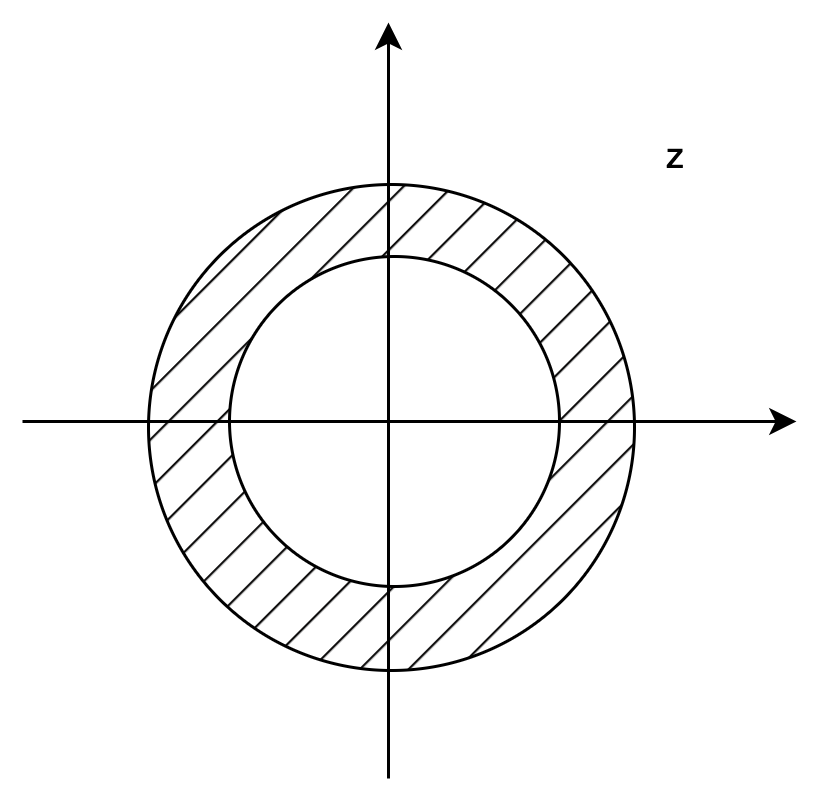
例:双边序列\(\displaystyle X(z) = \sum _{n=-\infty }^{\infty }x[n]z^{-n}\)的收敛域。 任何双边序列都可以分解为因果序列和反因果序列的和,因此,双边序列的收敛域是因果序列和反因果序列收敛域的交集。即收敛区域是环状区域。
例:有限长序列\(\displaystyle x[n] = \delta[n]\)的收敛域。
\(\displaystyle X(z) = \sum_{n=-\infty}^{\infty} \delta[n]z^{-n} = 1\)
因此,该序列的收敛域为整个z平面。推广到有限长序列\(\displaystyle X(z) = \sum _{n=n_1 }^{n_2 }x[n]z^{-n}\)的收敛域,收敛区域为\(0 < |z| < \infty\),如果\(n_1>0\),则收敛域包括无穷远点,如果\(n_2<0\),则收敛域包括零点。
Z的反变换
Z变换的反变换定义为:
\(\displaystyle {\displaystyle x[n]={\mathcal {Z}}^{-1}\{X(z)\}={\frac {1}{2\pi j}}\oint_{C}X(z)z^{n-1}dz }\)
其中C是X(z)收敛域内的逆时针闭合曲线。
围线积分法(留数法)
围线积分法是一种用于计算复变函数在沿着一个闭合曲线上积分的方法,通常用于复数分析和复积分的计算。 围线c将\(X(z)z^{n-1}\)的极点分为围线内的极点和围线外的极点。如果利用围线内的极点\(z_k\)来计算x[n],则有:
\(\displaystyle \frac {1}{2\pi j} \oint_{C}X(z)z^{n-1}dz = \sum_k Res[X(z)z^{n-1}]_{z=z_k} \)
此时,\(x[n]\)的值等于围线内的极点的留数之和。
如果利用围线外的极点\(z_m\)来计算x[n],则有:
\(\displaystyle {\frac {1}{2\pi j}}\oint_{C}X(z)z^{n-1}dz = -\sum_kRes[X(z)z^{n-1}]_{z=z_m}\)
此时,\(x[n]\)的值等于围线外的极点的留数之和的负数。如果要利用围线外的极点来计算,同时需要上面式子中的\(X(z)z^{n-1}\)的分母多项式中z的阶次比分子多项式z的阶次高二阶或二阶以上。
留数的计算公式为:
\(\displaystyle \sum_kRes[X(z)z^{n-1}]_{z=z_k} = [(z-z_k)X(z)z^{n-1}]|_{z=z_k}\)
具体是选择用围线外的极点还是围线内的极点来计算,取决于实际解题过程中哪种方法计算更简单。
例:\(X(z)=\frac{1}{(1-\frac{1}{4} z^{-1})(1-\frac{1}{2} z^{-1})}\),其中\(|z|>\frac{1}{2}\),求\(x[n]\)。
解:首先由收敛域可以确定该序列为因果序列,因此\(n \geq 0\);
\(\displaystyle X(z)z^{n-1}=\frac{1}{(1-\frac{1}{4} z^{-1})(1-\frac{1}{2} z^{-1})}z^{n-1}=\frac{1}{(z-\frac{1}{4})(z-\frac{1}{2})}z^{n+1}\)
在收敛域内画一条围线c,c将\(X(z)z^{n-1}\)的极点分成了围线内的极点和围线外的极点,围线内的极点为\(z=\frac{1}{4}\)和\(z=\frac{1}{2}\),围线外的极点为\(z=\infty\)(当n>1时,\(z=\infty\)为极点);
考虑到计算的简便性,选择用围线内的极点来计算 $\( \begin{split} x[n] & = Res[X(z)z^{n-1}]_{z=\frac{1}{4}}+Res[X(z)z^{n-1}]_{z=\frac{1}{2}} \\ & = (z-\frac{1}{4})\frac{1}{(z-\frac{1}{4})(z-\frac{1}{2})}z^{n+1}|_{z=\frac{1}{4}}+(z-\frac{1}{2})\frac{1}{(z-\frac{1}{4})(z-\frac{1}{2})}z^{n+1}|_{z=\frac{1}{2}} \\ & = 2(\frac{1}{2})^n-(\frac{1}{4})^n, n \geq 0 \end{split} \)$
也是可以写成:
\(\displaystyle x[n]=-(\frac{1}{4})^nu[n]+2(\frac{1}{2})^nu[n]\)
部分分式法
在讲解部分分式法之前,我们先看一下几种常见序列的Z变换:
下面利用部分分式法来求解上面的例题。
首先由收敛域可以确定该序列为因果序列,因此\(n \geq 0\);
由极点可以将\(X(z)\)分成\(\displaystyle X(z)=\frac{A}{(1-\frac{1}{4} z^{-1})}+\frac{B}{(1-\frac{1}{2} z^{-1})}\)
系数可以下列的留数定理求解:
\(\displaystyle A=(1-\frac{1}{4} z^{-1})X(z)|_{z=\frac{1}{4}} = -1\)
\(\displaystyle B=(1-\frac{1}{2} z^{-1})X(z)|_{z=\frac{1}{2}} = 2\)
\(\displaystyle X(z)=\frac{-1}{(1-\frac{1}{4} z^{-1})}+\frac{2}{(1-\frac{1}{2} z^{-1})}\)
\(\displaystyle x[n]=-(\frac{1}{4})^nu[n]+2(\frac{1}{2})^nu[n]\)
Z变换的性质
下表列出了Z变换的一些常见性质,更多的性质可以参考相关的教材。
Z变换的性质需要注意到收敛域的问题。