#! https://zhuanlan.zhihu.com/p/660491343

分段卷积(Block Convolution)

离散时间信号进入系统后，输出是输入和系统单位抽样响应的卷积和。在很多实际的系统中，比如语言信号，信号的长度很长，如果我们等到所有的信号存储下来再去跟单位抽样响应做卷积和，就很引起很大的延迟，另外，卷积运算我们通常是通过频域的快速傅里叶变换来计算的，这样会造成短的单位抽样序列补上非常多的零，也是不经济的。因此，我们通常用分段卷积的方式来进行计算。

分段卷积的思想是将长的序列分成若干段，每段的长度和单位抽样响应的长度同一数量级，然后对每段序列分别与单位抽样响应做卷积和，最后将所有的结果按某种方式拼接起来。这样做的好处是，每段序列的长度都不长，可以很方便的存储，而且每段序列的长度和单位抽样响应的长度同一数量级，可以很方便的进行频域的快速傅里叶变换。我们通常利用下面两种方式实施分段卷积。

重叠相加法

重叠相加法的思想是将长的序列\(x[n]\)分成长度为\(L\)的小段，长度\(L\)跟单位抽样响应\(h[n]\)的长度\(M\)同一数量级，然后每一段跟\(h[n]\)做线性卷积，线性卷积结果的长度为\(L+M-1\)，将前一段线性卷积结果的后\(M-1\)位跟后一段线性卷积结果的前\(M-1\)位重叠相加，最后将所有的小段序列的卷积结果相连，就得到了线性卷积的结果。

每一小段线性卷积可以用周期为\(N=L+M-1\)的圆周卷积来等效，然后再利用DFT变换来求解。

例：两个序列\(x[n] = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)和\(h[n] = \{1, 2\}\)，用重叠相加法计算两个序列的线性卷积和。

首先将长序列\(x[n]\)分成长度\(L=3\)的小段序列，即：

\(x_1[n] = \{1, 2, 3\}\)， \(x_2[n] = \{4, 5, 6\}\)， \(x_3[n] = \{7, 8, 9\}\)

分别计算每一小段序列与单位抽样响应的卷积和（可以通过线性卷积和圆周卷积的等效，再利用DFT变换来求解），得到：

\(y_1[n] = x_1[n]*h[n] = \{1, 4, 7, 6\}\)

\(y_2[n] = x_2[n]*h[n] = \{4, 13, 16, 12\}\)

\(y_3[n] = x_3[n]*h[n] = \{7, 22, 25, 18\}\)

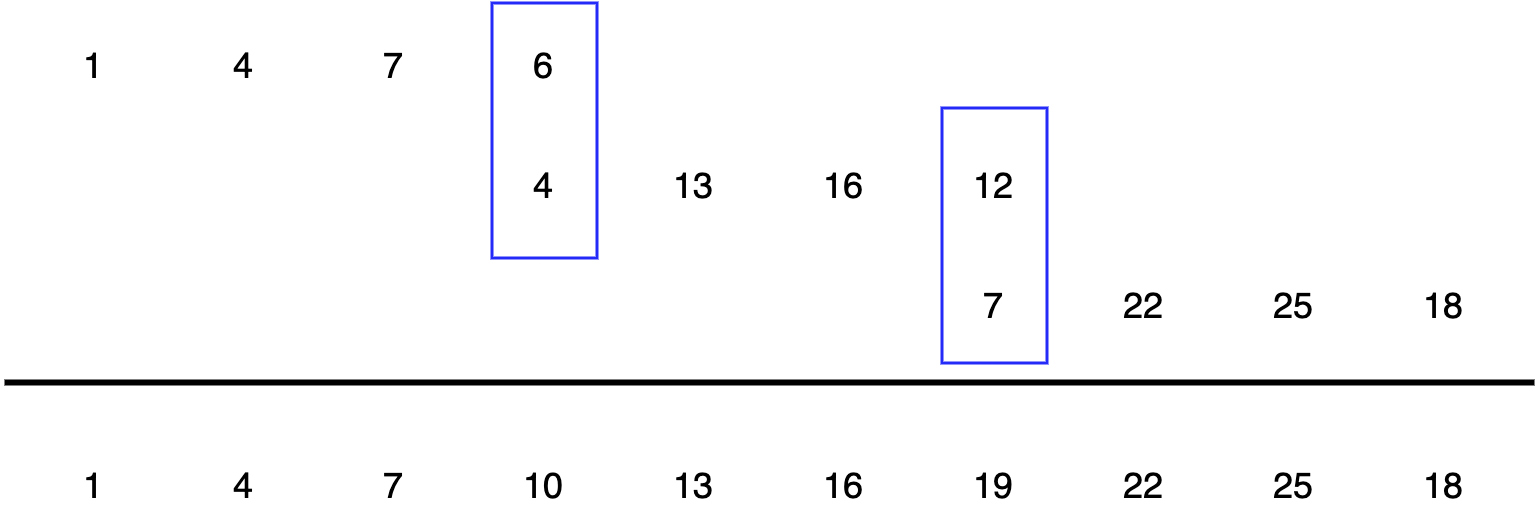
将每一小段序列的卷积结果的最后一位和下一小段序列的卷积结果的前一位重叠相加，得到最终的卷积结果，示意图如下：

重叠保留法

重叠保留法同样是将长的序列\(x[n]\)分成长度为\(L\)的小段，只是每一小段序列的前面加上前一小段序列的末尾\(M-1\)位（这里\(M\)是单位抽样信号的长度），这样每一小段序列的长度都是\(L+M-1\)(对于第一段序列，序列的前面加上\(M-1\)个零点），然后每一小段序列跟单位抽样响应\(h[n]\)做\(N=L+M-1\)点的圆周卷积，其圆周卷积的结果再去掉前面\(M-1\)个点，这样就得到了每一小段序列的卷积结果，最后将所有的小段序列的卷积结果相连，就得到了线性卷积的结果。

例：两个序列\(x[n] = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)和\(h[n] = \{1, 2\}\)，用重叠保留法计算两个序列的线性卷积和。

重叠相加法将长序列\(x[n]\)分成长度\(L=3\)的小段序列，但是在每小段序列的前面加上前一小段序列的末尾\(M-1=1\)位，即：

\(x_1[n] = \{0, 1, 2, 3\}\)， \(x_2[n] = \{3, 4, 5, 6\}\)， \(x_3[n] = \{6, 7, 8, 9\}\), \(x_4[n] = \{9, 0, 0, 0\}\)

分别计算每一段序列与单位抽样响应的圆周卷积，得到：

\(y_1[n] = x_1[n] \circledast h[n] = \{6, 1, 4, 7\}\)

\(y_2[n] = x_2[n] \circledast h[n] = \{15, 10, 13, 16\}\)

\(y_3[n] = x_3[n] \circledast h[n] = \{24, 19, 22, 25\}\)

\(y_4[n] = x_4[n] \circledast h[n] = \{9, 18, 0, 0\}\)

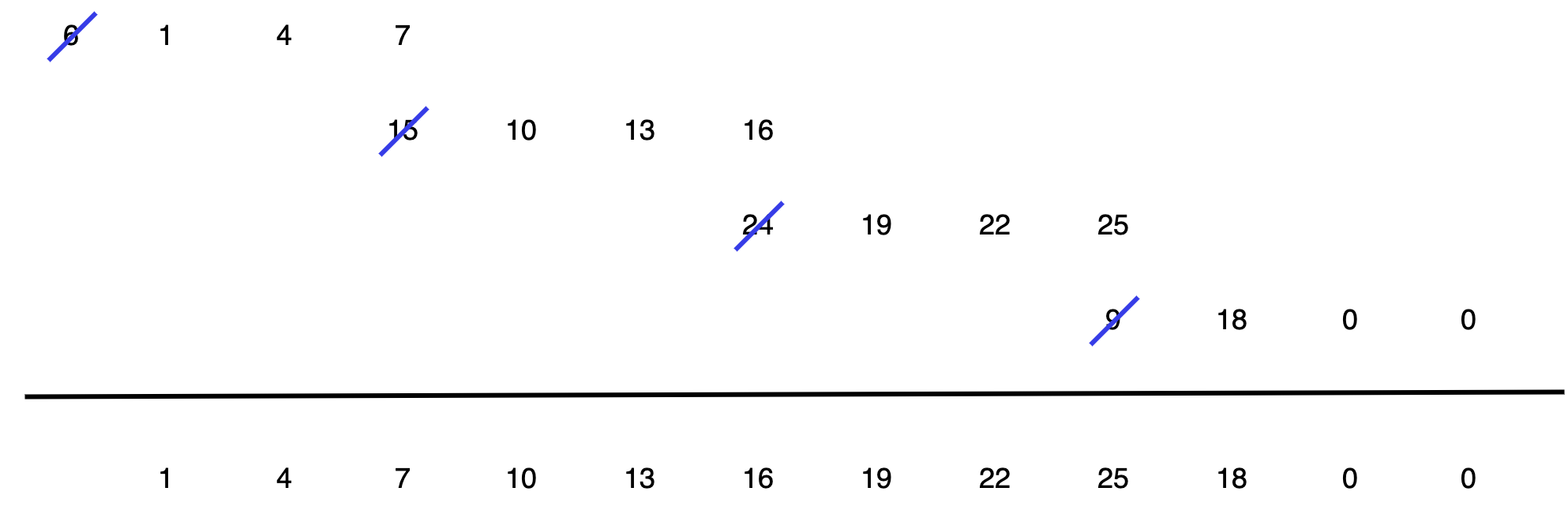
再将每一小段序列和单位抽样响应的卷积结果去掉前面\(M-1=1\)个点，然后再相连就得到最后的结果，示意图如下：