#! https://zhuanlan.zhihu.com/p/665349466
数字数据格式
引言
在数字信号处理中,有多种方式可以在计算机硬件上表示数值数据。这些被称为数据格式的表示方法对于任何给定的信号处理算法的准确性和实现的便利性都有深远影响。简单的数据格式虽然简化了硬件的设计,但也存在数字表示范围有限和计算误差敏感的缺点。而更复杂的数据格式在硬件上实现起来可能较为困难,但它们允许我们操作非常大或非常小的数字,并且还可以避免很多数字运算问题。
在本章中,我们将介绍最常见类型的定点数据格式,并展示它们何时以及为什么会被使用。我们也将涵盖浮点二进制格式这个有趣主题。
定点二进制格式
在数学中,正数(包括零)被表示为无符号数。也就是说,我们不在它们前面加上\(+\)号来显示它们是正数。但是,在处理负数时,我们使用一个\(-\)号来表示该数为负值。
然而,在数字电路中,并没有提供将加号或者负号放到数字前面的方法,因为数字系统使用以\(0\)和\(1\)表示的二进制数进行操作。在微电子学中,这些\(0\)和\(1\)一起使用时被称为比特(BInary digiT 的缩写),可分为几种不同大小的数字,它们的通用名称是字节(byte)或字(word)。
8位二进制数(一个字节)可以具有从0到255的值范围,即\(2^8 = 256\)种不同的比特组合形成一个单独的8位字节。所以例如一个无符号二进制数转换成十进制数表示为:\({01001101}_2 = 64 + 8 + 4 + 1 = 77_{10}\)。但是数字系统和计算机必须能够使用和操作负数以及正数。
通常情况下,数学上的数字由符号和值(大小)组成;其中符号表示该数字是否为正(+)或负(-),而值表示数字的大小,例如23、+156或-274。以这种方式呈现数字被称为“符号-幅度”表示法,因为最左边的数字可以用来表示符号,剩余的数字表示数值或幅度。
符号-幅度表示法
对于有符号的二进制数,最左边的位叫做最高有效位(Most Significant Bit, MSB)被用作符号位。如果符号位为\(0\),表示数值为正。如果符号位为\(1\),则数字为负值。数字中的其余位以通常的无符号二进制数格式表示二进制数的大小。
那么我们可以看到,符号-幅度(SM)记数法是通过将n位总数分为两部分来存储正负值的:1 位表示符号,\(n-1\) 位表示数值,即纯二进制数。例如,十进制数 \(53\) 可以用 \(8\) 位有符号二进制数表示如下。

符号-幅度二级制格式中,一个b位字长的二进制数仅能够表示大小为\([-2^{b-1}+1, 2^{b-1}-1]\)的数值范围。比如一个8位符号-幅度二进制数可以表示的最大正值和最大负值是\(127\)和\(-127\)。
使用这种符号-幅度方法可能导致两个不同的位模式具有相同的二进制值。例如,+0和-0将分别作为带符号的4位二进制数表示为\({0000}_2\)和\({1000}_2\),这可能给计算机和数字系统带来很大的复杂性。
1的补码二进制格式
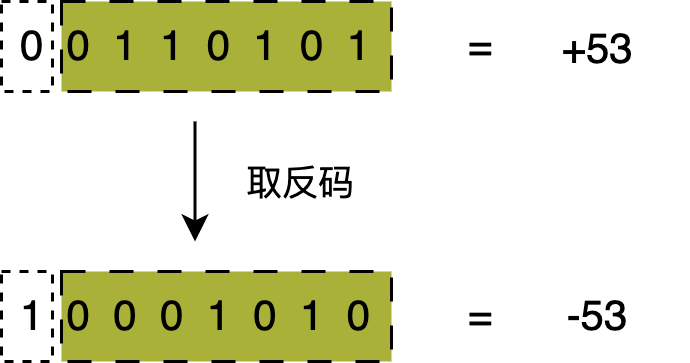
为了避免符号-幅度二进制格式中的这种复杂性,我们可以使用1的补码二进制格式。在这种格式中,正数的二进制值跟符号-幅度方法是一样的,负数的二进制值是其绝对值的二进制值的补码。补码是通过将数字的每个位取反(0变为1,1变为0)。例如,十进制数\(-53\)的1的补码二进制格式求解过程如下:十进制数\(-53\)的绝对值是\(53\),首先将其表示成二进制数的格式,然后将所有的0变成1,所有的1变成0,如下图所示。
1的补码表示同样存在一个问题,就是在这种表示法中,零也有两种表示方式,一个是正零\({0000}_2\),另一个是负零\({1111}_2\)。
2的补码二进制格式
从硬件设计的角度来看,2的补码二进制格式是最方便的数据格式,也是计算机硬件中最常用的二进制数据格式。在这种格式中,正数的二进制值跟符号-幅度方法是一样的,负数的二进制值是其绝对值的二进制值的补码。补码是通过将数字的每个位取反(0变为1,1变为0)并将结果加1来计算的。例如,十进制数\(-53_2的补码二进制格式求解过程如下:十进制数\)-53\(的绝对值是\)53$,首先将其表示成二进制数的格式,然后取反码,再对其最小有效位(Least Significant Bit, LSB)实行加1的运算,如下图所示。
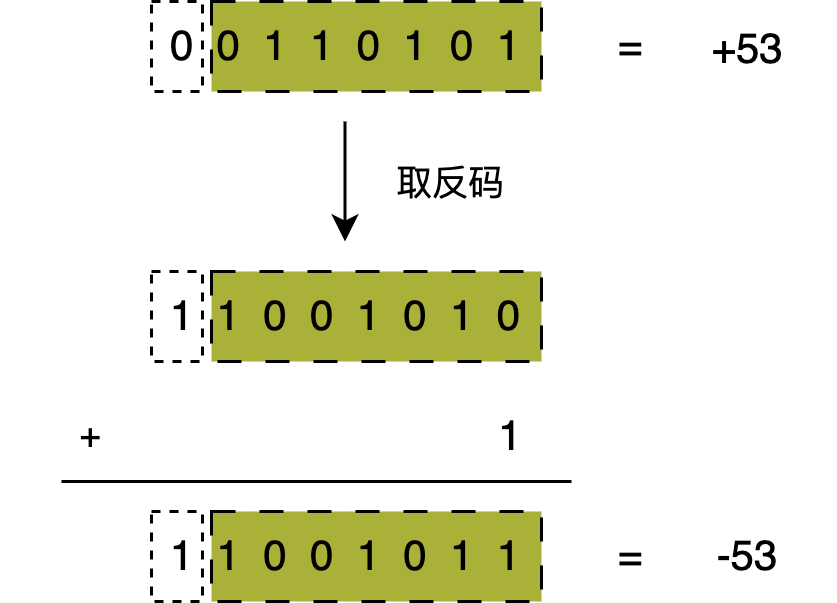
2的补码表示法的优势:在2的补码表示法中,一个b位字长的二进制数能够表示大小为\([-2^{b-1}, 2^{b-1}-1]\)的数值范围。比如一个8位2的补码二进制数可以表示的最大正值和最大负值是\(127\)和\(-128\)。
2的补码表示法使计算机可以使用相同的逻辑加法器来进行加法和减法运算。
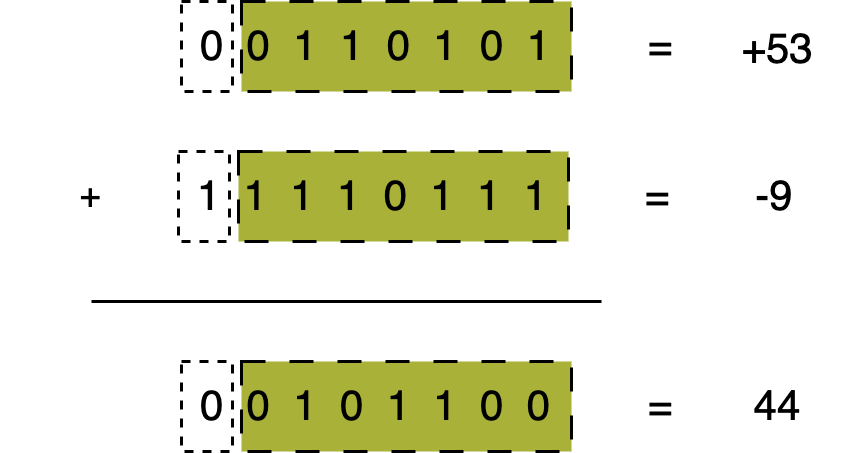
例:\(53-9=44\)在2的补码二进制格式中的计算如下:
偏移二进制格式
偏移二进制数据格式并不像2的补码二进制格式那样常用,但是在某些硬件设备中,仍然能够见到它。偏移二进制数是通过从无符号二进制数减去一个偏移量\(2^b-1\)来表示的。下表给出了各种二进制格式的比较:
等价十进制 |
符号-幅度 |
1的补码二进制 |
2的补码二进制 |
偏移二进制 |
|---|---|---|---|---|
7 |
0111 |
0111 |
0111 |
1111 |
6 |
0110 |
0110 |
0110 |
1110 |
5 |
0101 |
0101 |
0101 |
1101 |
4 |
0100 |
0100 |
0100 |
1100 |
3 |
0011 |
0011 |
0011 |
1011 |
2 |
0010 |
0010 |
0010 |
1010 |
1 |
0001 |
0001 |
0001 |
1001 |
+0 |
0000 |
0000 |
0000 |
1000 |
-0 |
1000 |
0111 |
- |
- |
-1 |
1001 |
1110 |
1111 |
0111 |
-2 |
1010 |
1101 |
1110 |
0110 |
-3 |
1011 |
1100 |
1101 |
0101 |
-4 |
1100 |
1011 |
1100 |
0100 |
-5 |
1101 |
1010 |
1011 |
0011 |
-6 |
1110 |
1001 |
1010 |
0010 |
-7 |
1111 |
1000 |
1001 |
0001 |
-8 |
- |
- |
1000 |
0000 |
我们可以通过对数的最高有效位取反码而实现2的补码二进制格式和偏移二进制格式之间的互相转换。
浮点二进制格式
我们以IEEE 754标准为例来介绍浮点二进制格式。IEEE 754为许多CPU与浮点运算器所采用。
浮点数的实际值等于符号位(sign bit)乘以指数值再乘以小数值
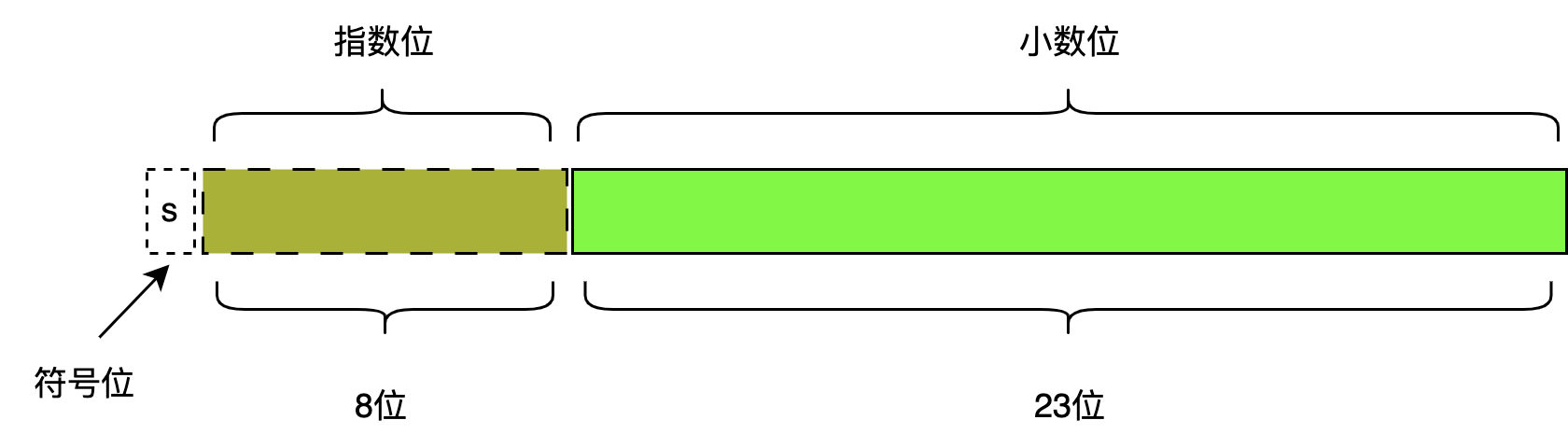
下面描述了一个单精度32位浮点数的表示
第1位是符号位表示正负,中间8位是指数位(在IEEE 754中用偏移二进制格式表示),后23位表示小数位(有效数位是24位)。
通常小数位由24位表示,但由于第1位一定是1,所以第1位的1可以省略,只需要存储后23位即可。这样有效数位就变成了23位。这23位由符号-幅度表示法表示。我们用图形表示如下:
例:十进制3.6875的单精度浮点数表示如下:
首先将十进制转化为成二进制数\(11.1011\),然后将其标准化为\(0.111011\times2^2\),其中指数位十进制是\(2\),用偏移二进制格式表示如下图,小数位其中的第一个在存储中可以省略,那么只要存储\(11011\)即可。最后将其表示成单精度浮点数的格式如下:
