#! https://zhuanlan.zhihu.com/p/658256428
圆周卷积与线性卷积
离散时间信号的线性卷积
给定两个离散时间信号\(x[n]\)和\(h[n]\),它们的线性卷积定义为:
\(\displaystyle y[n]=x[n]*h[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]\)
其中,\(*\)表示卷积运算,\(y[n]\)称为\(x[n]\)和\(h[n]\)的卷积和。
给定\(x[n]\)的信号长度为\(L_1\), \(h[n]\)的信号长度为\(L_2\),则卷积和\(y[n]\)的信号长度为\(L_1+L_2-1\)。
例:给定\(x[n]=\{1,3,5\}\),\(h[n]=\{1,2\}\),求\(x[n]\)和\(h[n]\)的卷积和\(y[n]\)。
方法一:我们用矩阵的形式来计算卷积和\(y[n]\),由于\(x[n]\)和\(h[n]\)的信号长度分别为3和2,所以\(y[n]\)的信号长度为\(L_1+L_2-1=4\),我们让\(y=[y[0],y[1],y[2],y[3]]^T\)是一个\(4\times1\)的列向量,则有:
其中,\(H\)是一个\(4\times3\)的变换矩阵。
如果单从矩阵计算来看,可以将\(h[n]\)通过补零扩展成一个\(4\times1\)的列向量,就是\(H\)的第一列,第二列是\(h[n]\)右移一位,第三列是\(h[n]\)右移两位,这样就可以很简便地把这个变换矩阵写出来。
方法二:我们也可以将\(h[n]\)等效成两个单位抽样序列的相加,即\(h[n]=\delta[n]+2\delta[n-1]\),于是\(y[n]=x[n]*h[n]=x[n]+2x[n-1]\),我们可以用图形的方式来表示卷积和的计算过程,如下图所示:
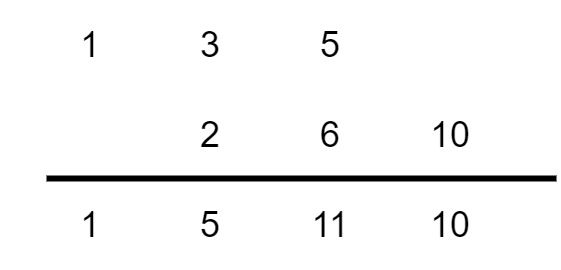
方法三:从以上推导可以看出如果我们设置\(x[n]\)和\(h[n]\)为多项式系数的向量,卷积和的运算也等于这两个多项式相乘的运算,即:
\(\displaystyle (x^2+3x+5)(x+2)=x^3+5x^2+11x+10\)
因此,多项式相乘后的结果的系数向量就是卷积和的结果。
离散时间信号的圆周卷积
给定两个离散时间信号\(x[n]\)和\(h[n]\),它们的圆周卷积定义为:
\(\displaystyle y[n]=x[n] \circledast h[n]=\sum_{k=0}^{N-1}x[k]h((n-k))_N R_N[n]\)
其中,\(R_N[n]\)是周期为\(N\)的矩形序列。
圆周卷积需要先给定一个周期\(N\),然后将两个信号的长度都扩展为\(N\);
圆周卷积假定两个离散时间信号隐含了周期性,先将其化为周期序列,再做周期卷积运算,然后再取出主值区间(即区间0到\(N-1\))的结果;
圆周卷积中序列的翻褶和移位均是循环翻褶和循环移位运算。
圆周卷积的结果\(y[n]\)的信号长度为\(N\)。
例:给定\(x[n]=\{1,3,5\}\),\(h[n]=\{1,2\}\),求\(x[n]\)和\(h[n]\)N点的圆周卷积和\(y[n]\)。
方法一:如果给定\(N=3\),我们将\(x[n]\)和\(h[n]\)的信号长度都扩展为\(3\),于是得到\(x[n]=\{1,3,5\}\),\(h[n]=\{1,2,0\}\),此时\(y[n]\)的信号长度为\(3\),我们让\(y=[y[0],y[1],y[2]]^T\)为\(3 \times 1\)的列向量,利用矩阵的形式计算如下:
如果给定\(N=4\),我们将\(x[n]\)和\(h[n]\)的信号长度都扩展为\(4\),得到\(x[n]=\{1,3,5,0\}\),\(h[n]=\{1,2,0,0\}\),\(y[n]\)的信号长度为\(4\),我们让\(y=[y[0],y[1],y[2],y[3]]^T\),利用矩阵的形式计算如下:
其中\(H\)是一个变换矩阵。\(H\)矩阵第一行为\(h[-n]\),是\(h[n]\)的循环翻褶,第二行为\(h[1-n]\)循环右移一位,以此类推,最后一行为\(h[N-1-n]\)循环右移\(N-1\)位。
如果从构造\(H\)矩阵来看,我们可以将\(h[n]\)通过补零扩展成一个\(N\times1\)的列向量,就是\(H\)的第一列,第二列是\(h[n]\)循环右移一位,以此类推,最后一列就是\(h[n]\)循环右移\(N-1\)位。
方法二:同样地,我们也可以将\(h[n]\)等效成两个单位抽样序列的相加,即\(h[n]=\delta[n]+2\delta[n-1]\),于是\(y[n]=x[n]\circledast h[n]=x[n]+2x((n-1))_N R_N(n)\),需要特别注意的是这个地方的移位是循环移位,我们可以用图形的方式来表示卷积和的计算过程,如下图所示:
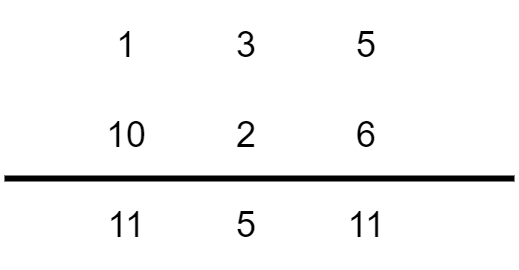
线性卷积和圆周卷积的关系
圆周卷积视为线性卷积以N为周期进行周期延拓后取主值区间的结果。
证明:根据圆周卷积的定义,有:
其中,\(y_l[n]\)是\(x[n]\)和\(h[n]\)的线性卷积和。
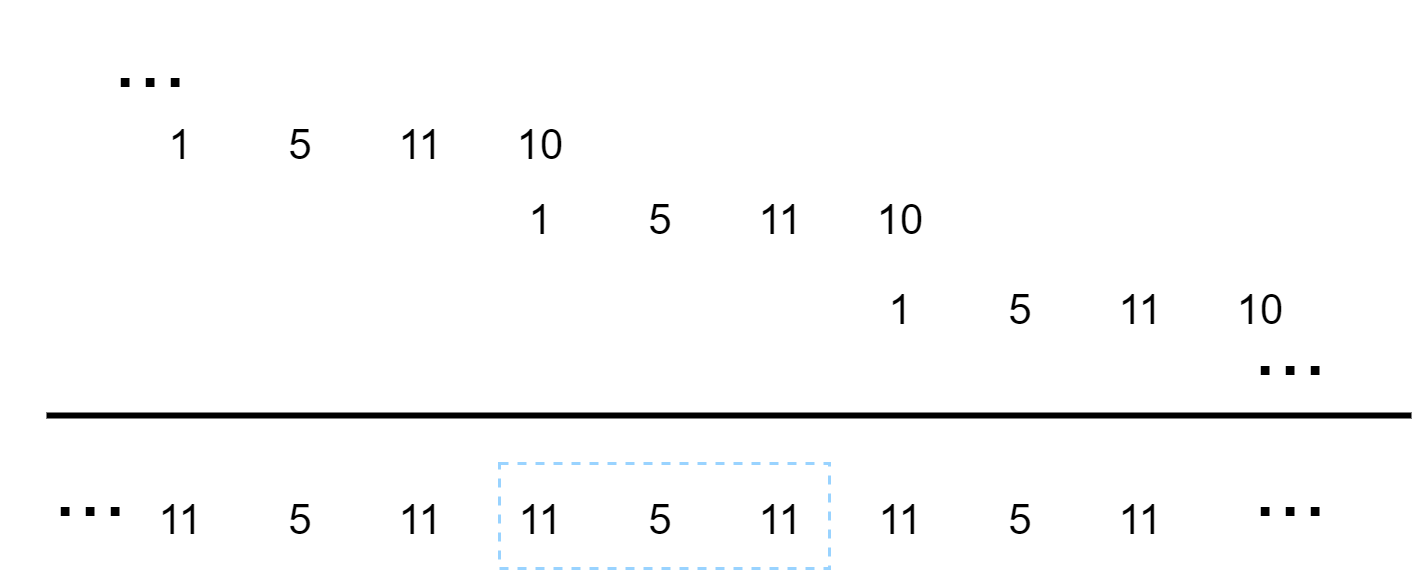
以之前的两个序列为例,如果我们做\(3\)点的圆周卷积,我们可以将\(x[n]\)和\(h[n]\)的线性卷积和\(y_l[n]\)的结果\(y_l=[1,5,11,10]\)以周期为\(3\)进行周期延拓,然后取扩展主值区间的值即为圆周卷积的结果。具体过程如下图所示:
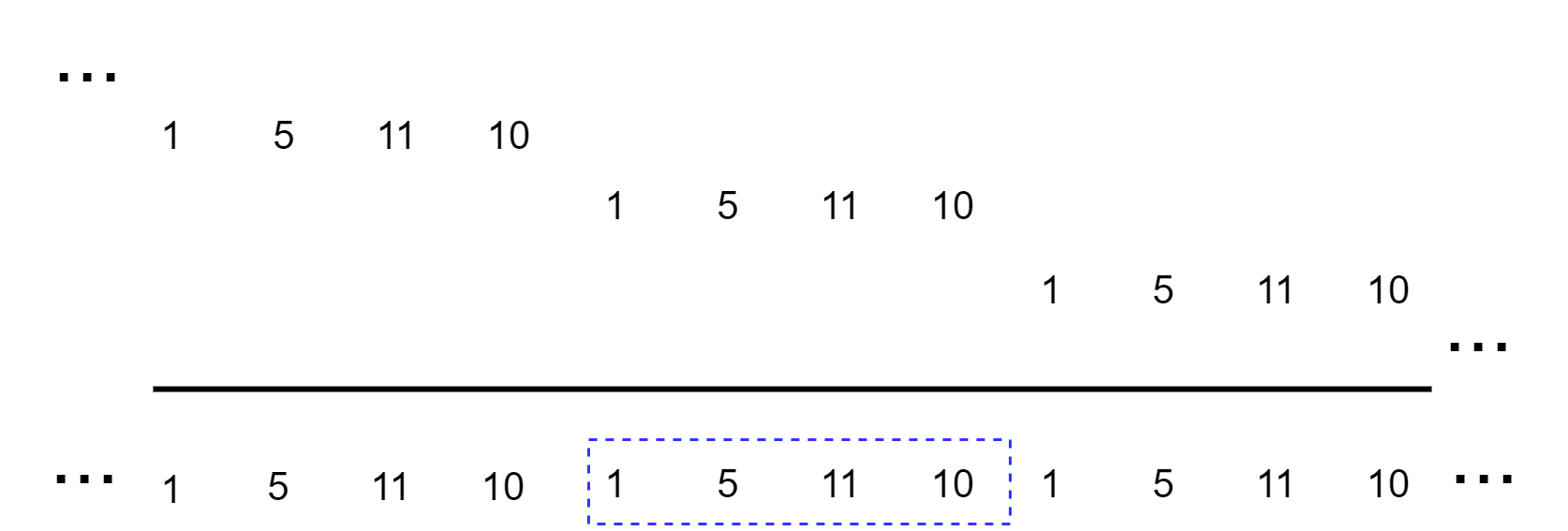
如果我们做\(4\)点的圆周卷积,我们可以将\(y_l[n]\)以周期为\(4\)进行周期延拓,然后取扩展主值区间的值即为圆周卷积的结果。具体过程如下图所示:
从上面的证明和图示可以看出,如果要让两个序列的线性卷积和圆周卷积计算结果一致,则圆周卷积的周期\(N\)必须大于等于两个序列的长度之和减一,即\(N \geq L_1+L_2-1\)。只有满足上面的条件,线性卷积在做周期延拓的时候,才不会有时域上的混叠,从而保证了圆周卷积和线性卷积的结果一致。
为什么要用圆周卷积去计算线性卷积
当一个离散时间信号进入一个线性时不变系统,系统的单位抽样响应为\(h[n]\),输入信号为\(x[n]\),则系统的输出为:
\(\displaystyle y[n]=x[n]*h[n]\)
此时的卷积为线性卷积。
在DFT变换中,两个信号时域的圆周卷积和在频域上等于两个信号的乘积,即:
\(\displaystyle x[n] \circledast h[n] \Leftrightarrow X[k]H[k]\)
此时的卷积为圆周卷积。卷积和的运算比较复杂,而DFT变换的正变换和反变换都有快速傅里叶(FFT)算法。如果我们将线性卷积转换为圆周卷积,就可以利用DFT性质将卷积运算转换成乘积运算,同时也可以利用到FFT算法,从而提高计算效率。