#! https://zhuanlan.zhihu.com/p/657549897
吉布斯现象(gibbs phenomenon)
存在不连续跳跃点的周期函数由傅里叶级数去表示时,在不连续的跳跃点附近会出现振荡现象,这种现象称为吉布斯现象。
例:周期的方波信号,在第一个周期内其数学表达式如下:
\( \begin{aligned} f(t) = \begin{cases} 1, & |t| \leq \tau/2 \\ 0, & \tau/2 < |t| < T/2 \end{cases} \end{aligned} \)
其傅里叶级数如下:
\(\displaystyle c_n = \frac{1}{T}\frac{\sin\left(\frac{n \Omega_0 \tau}{2}\right)}{n \Omega_0 \tau / 2}\)
周期方波信号傅里叶级数展开表达式如下:
\(\displaystyle x(t) = \sum_{n=-\infty}^{\infty}c_n e^{i n \Omega_0 t}=\sum_{n=-\infty}^{\infty}\frac{1}{T}\frac{\sin\left(\frac{n \Omega_0 \tau}{2}\right)}{n \Omega_0 \tau / 2}e^{i n \Omega_0 t}\)
通常实际情形中,我们只能取有限项,用有限项求和得到:
\(\displaystyle x_M(t) = \sum_{n=-M}^{M}c_n e^{i n \Omega_0 t}\)
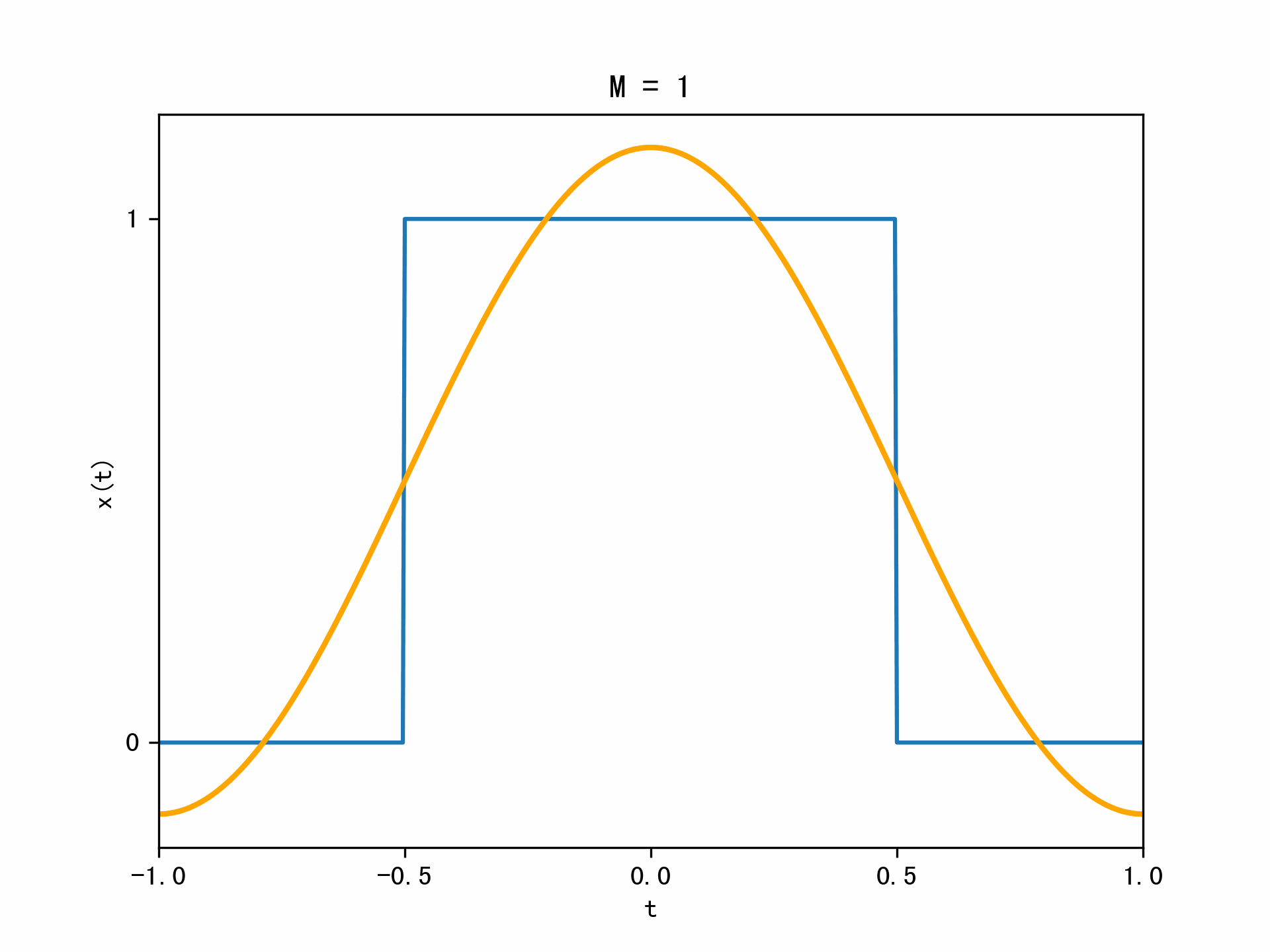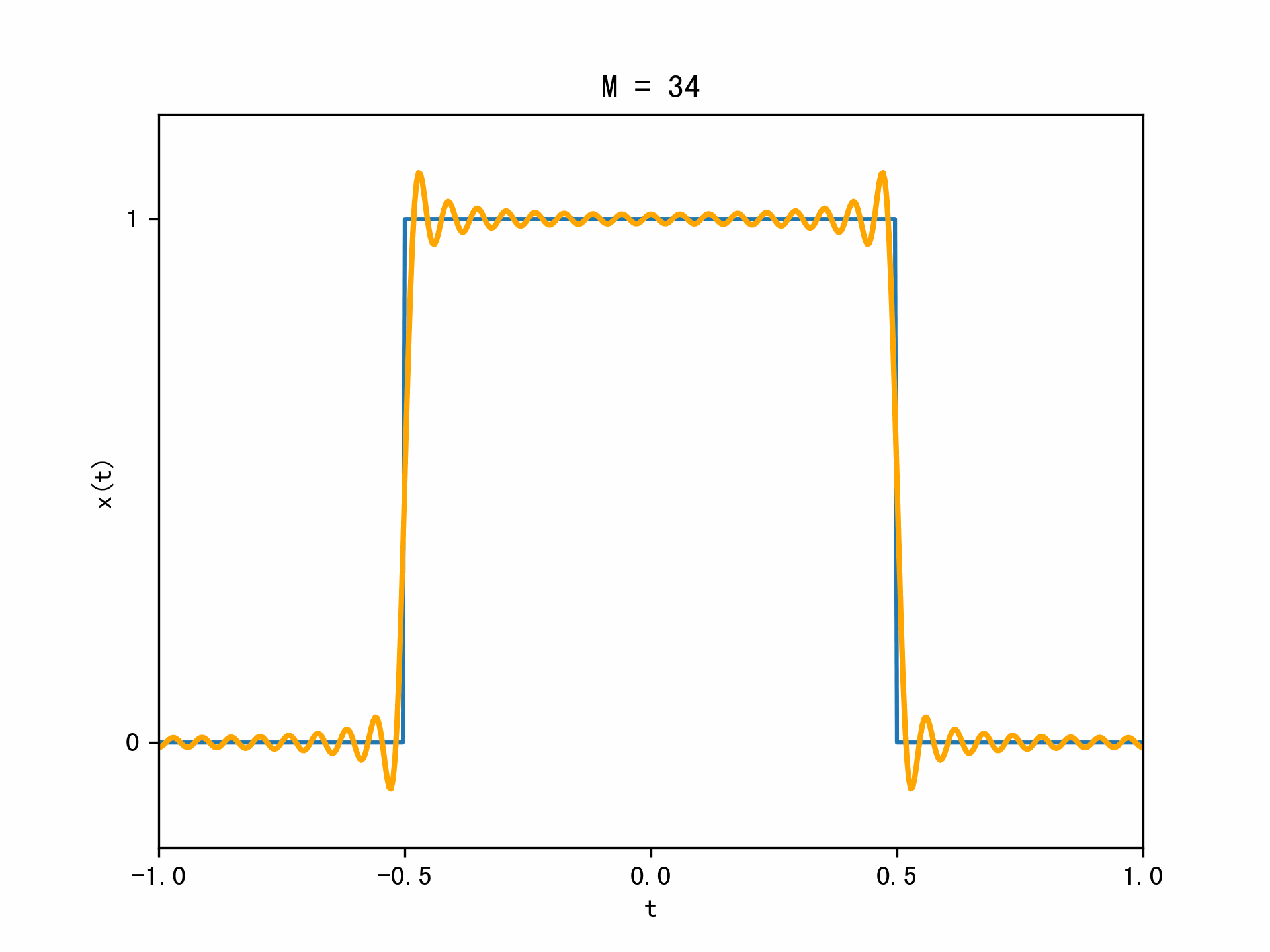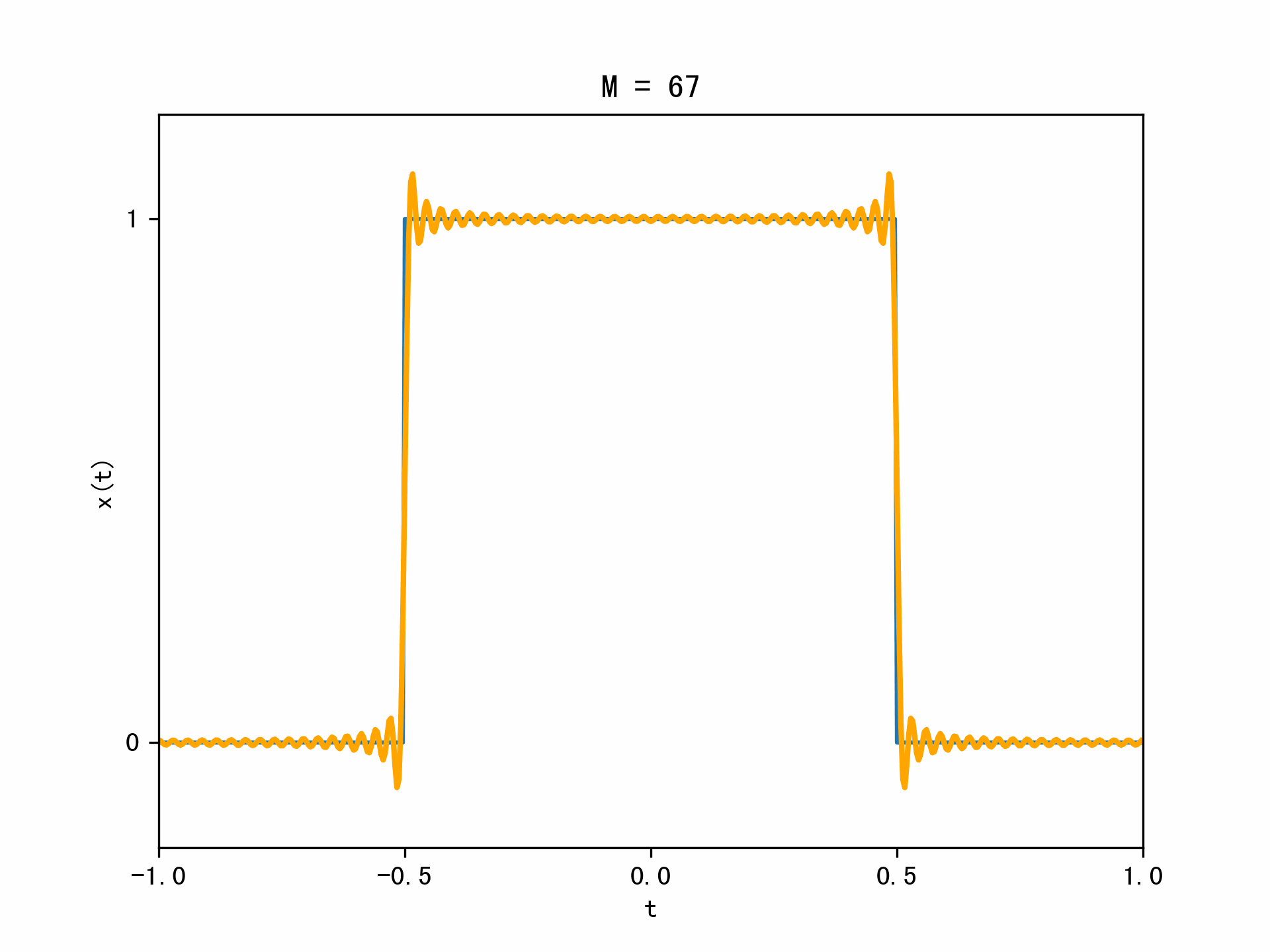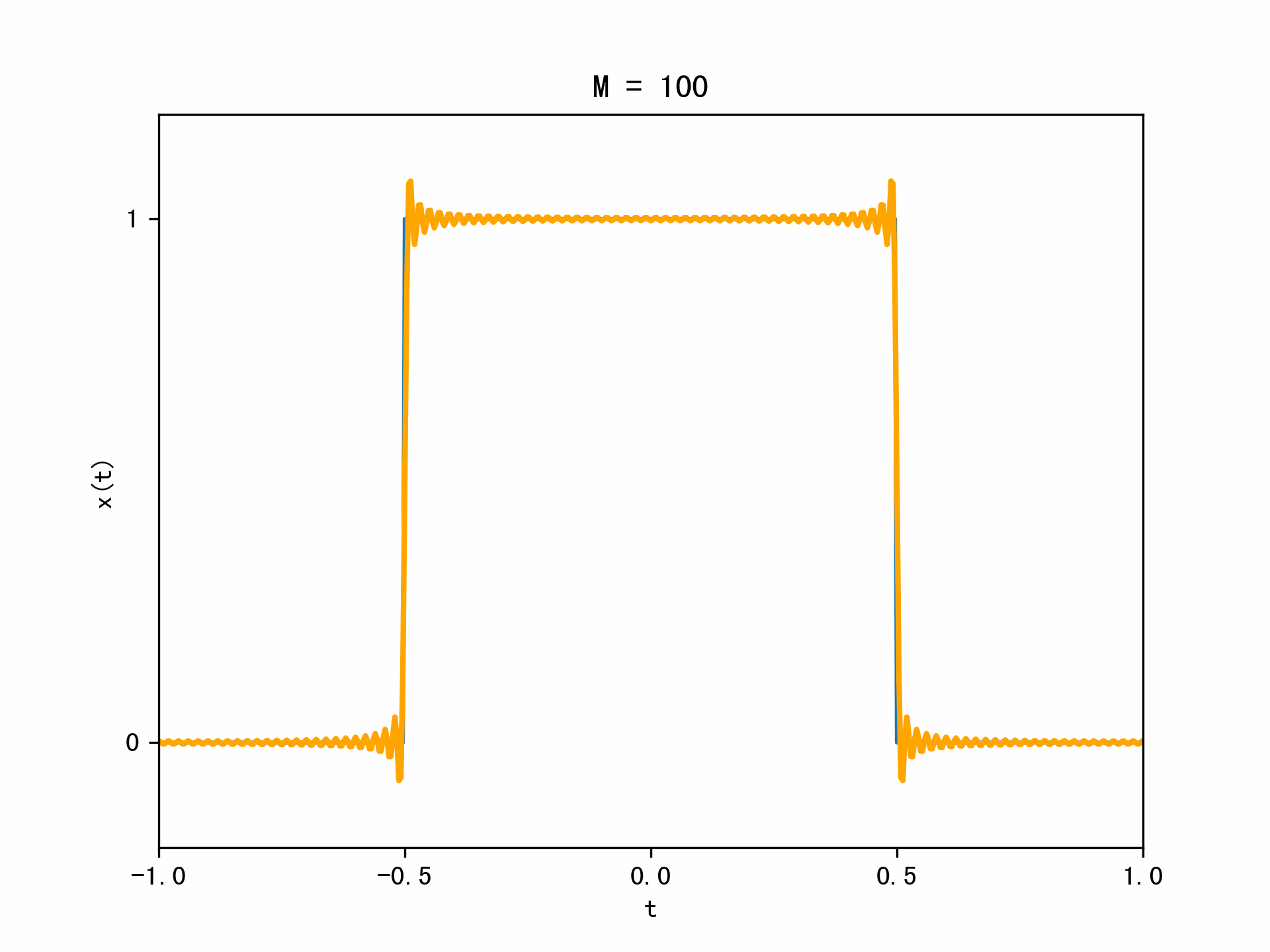
我们用\(x_M(t)\)来近似\(x(t)\),下图表示了当\(M\)取不同值时,\(x_M(t)\)与\(x(t)\)的近似程度。
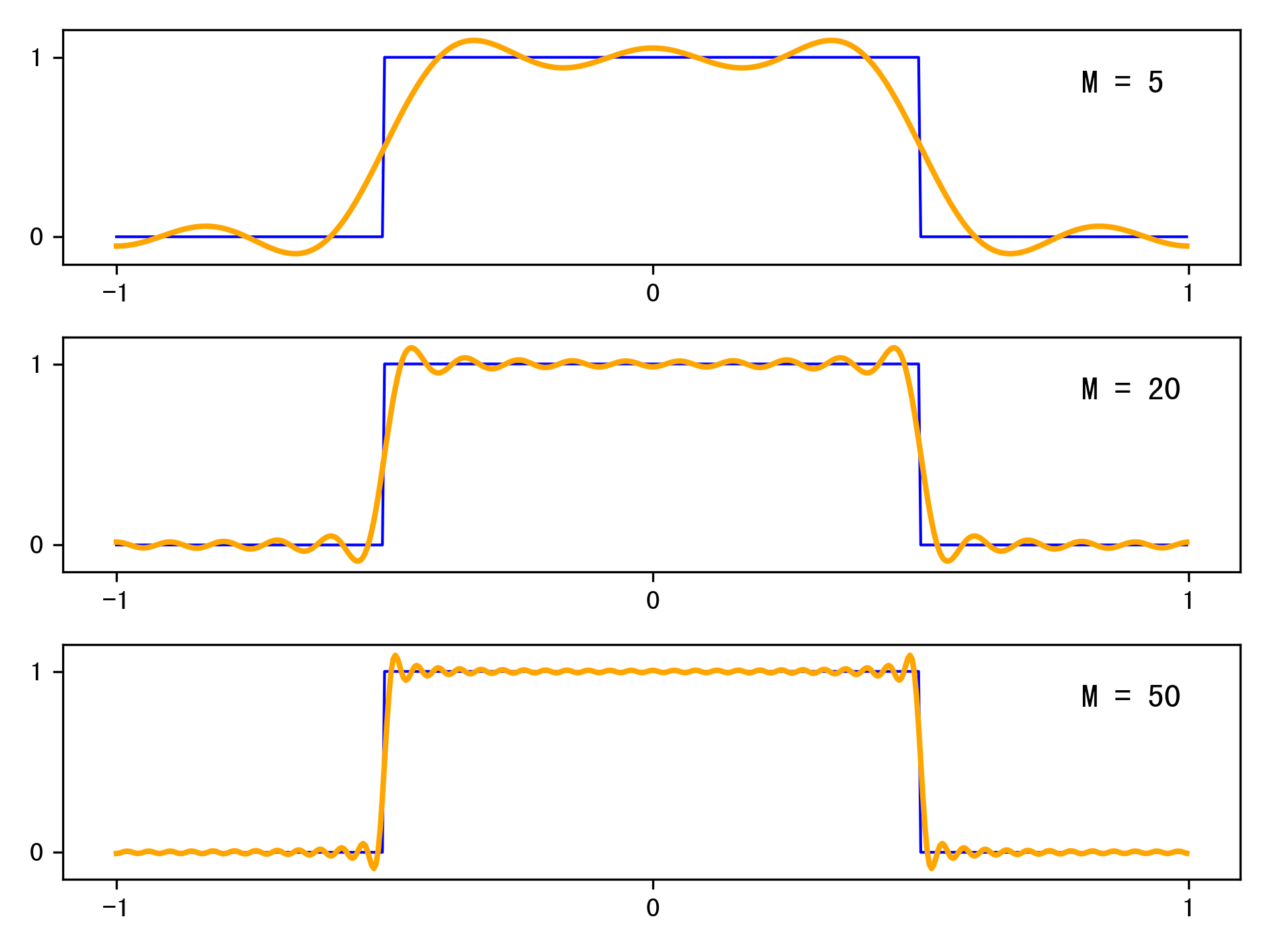
在跳跃的不连续点上出现振荡,随着\(M\)的增大,振荡向跳跃点靠近,但是振荡的幅度不会减小;
利用均方收敛的概念,\(x(t)\)与\(x_M(t)\)的均方误差(能量误差)随着\(M\)趋向于无穷大而趋向于0。当均方收敛成立时,我们认为这两个信号是相同的。
下面用动态图的形式展示了吉布斯现象:
例:理想数字低通滤波器,其频率响应为:
\( H(e^{j\omega})= \begin{cases} 1, \qquad |\omega|< \omega_c,\\ 0, \qquad \omega_c<|\omega|\leq \pi\\ \end{cases} \)
根据离散时间傅里叶变换的定义,它可以由无穷多个谐波相关的复指数序列加权求和得到:
\(\displaystyle H(e^{j\omega}) = \sum_{n=-\infty}^{\infty}h[n]e^{-j\omega n}\)
其中,\(h[n] = \frac{\sin\omega_c n}{\pi n}\)。我们通常用有限项求和来近似\(H(e^{j\omega})\),即:
\(\displaystyle H_M(e^{j\omega}) = \sum_{n=-M}^{M}\frac{\sin\omega_c n}{\pi n}e^{-j\omega n}\)
下图表示了当\(M\)取不同值时,\(H_M(e^{j\omega})\)与\(H(e^{j\omega})\)的近似程度。
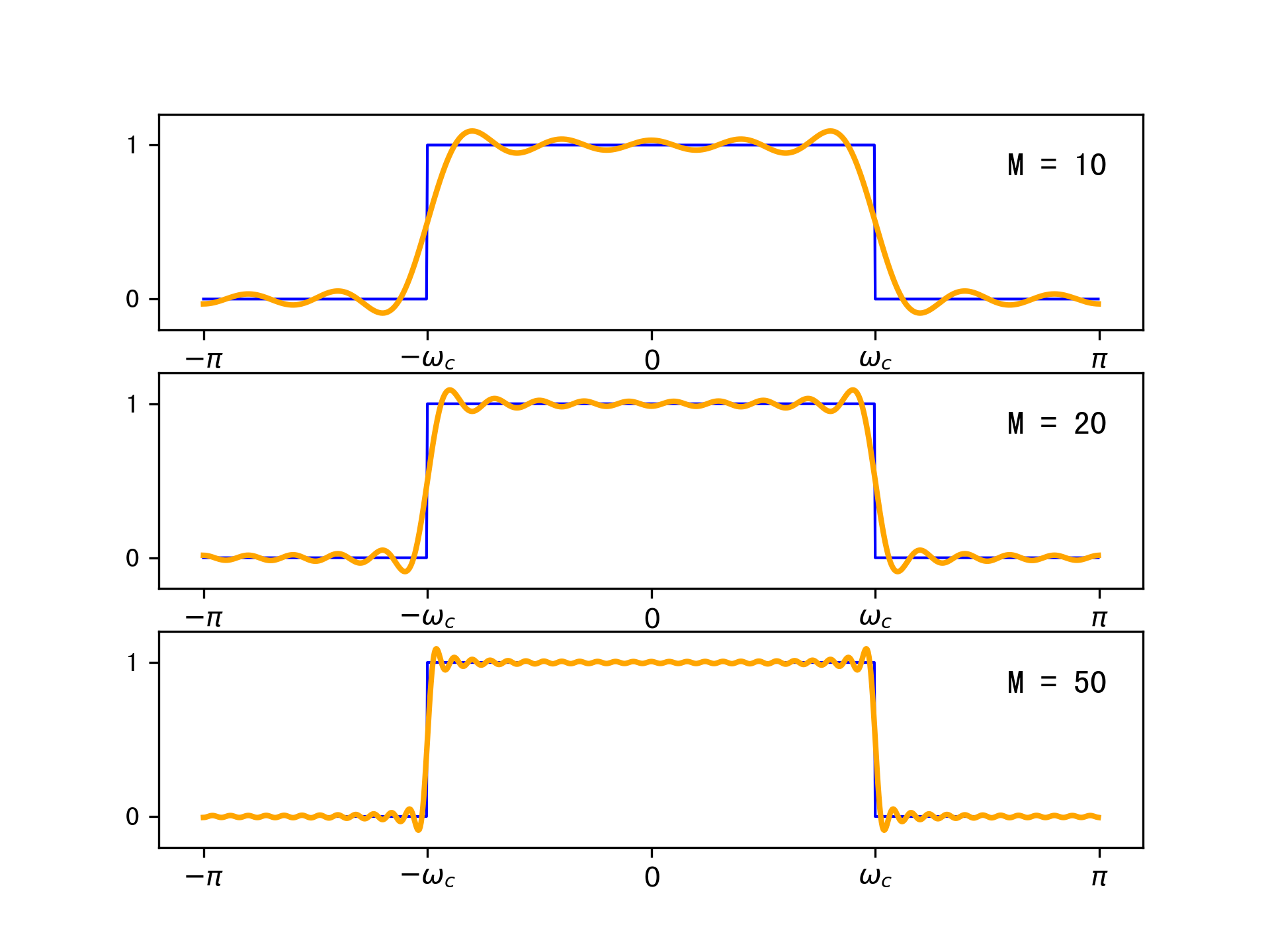
在频率上,具有跳跃不连续点的周期信号用复指数序列去表示时,同样会出现跟前面例子类似的gibbs现象。当下列表达式成立时,即均方收敛时,我们认为\(H(e^{j\omega})\)与\(H_M(e^{j\omega})\)是相同的。
下图动态的展示了数字低通滤波器用有限项复指数序列表示时出现的gibbs现象。
