#! https://zhuanlan.zhihu.com/p/667018849
模拟滤波器的设计
这一小节我们简单介绍几种模拟滤波器的设计:巴特沃斯滤波器、切比雪夫I型滤波器、切比雪夫II型滤波器、椭圆型滤波器。
巴特沃斯低通滤波器(Butterworth lowpass filter)
巴特沃斯低通滤波器的幅度平方函数为:
\(\displaystyle |H_c(j\Omega)|^2 = \frac{1}{1 + \left(\frac{\Omega}{\Omega_c}\right)^{2N}}\)
其中,\(\Omega_c\)为通带截止频率,\(N\)为滤波器的阶次。巴特沃斯滤波器的幅度平方函数用下图表示:
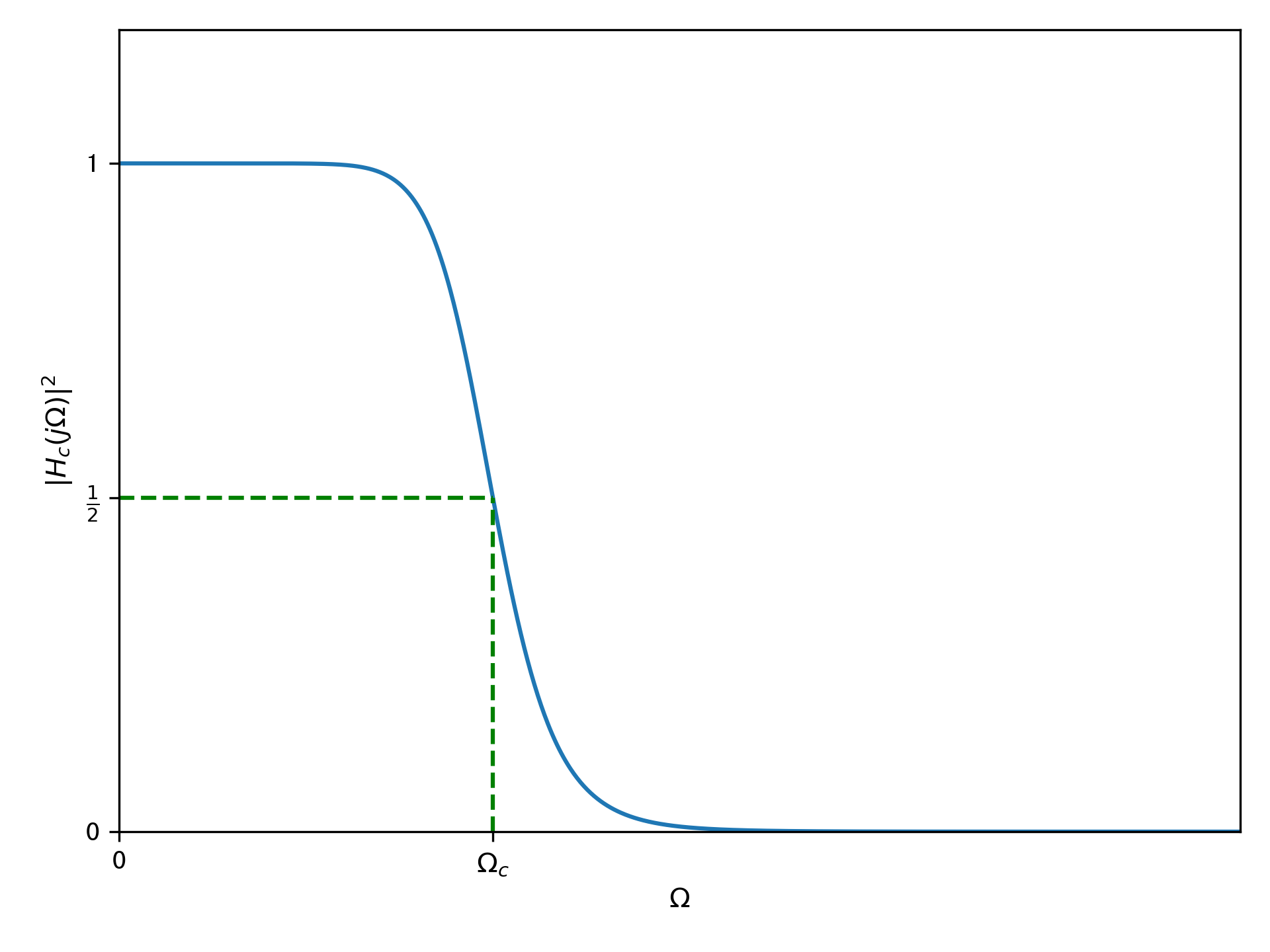
我们可以画出不同阶次的巴特沃斯低通滤波器的幅度响应曲线:
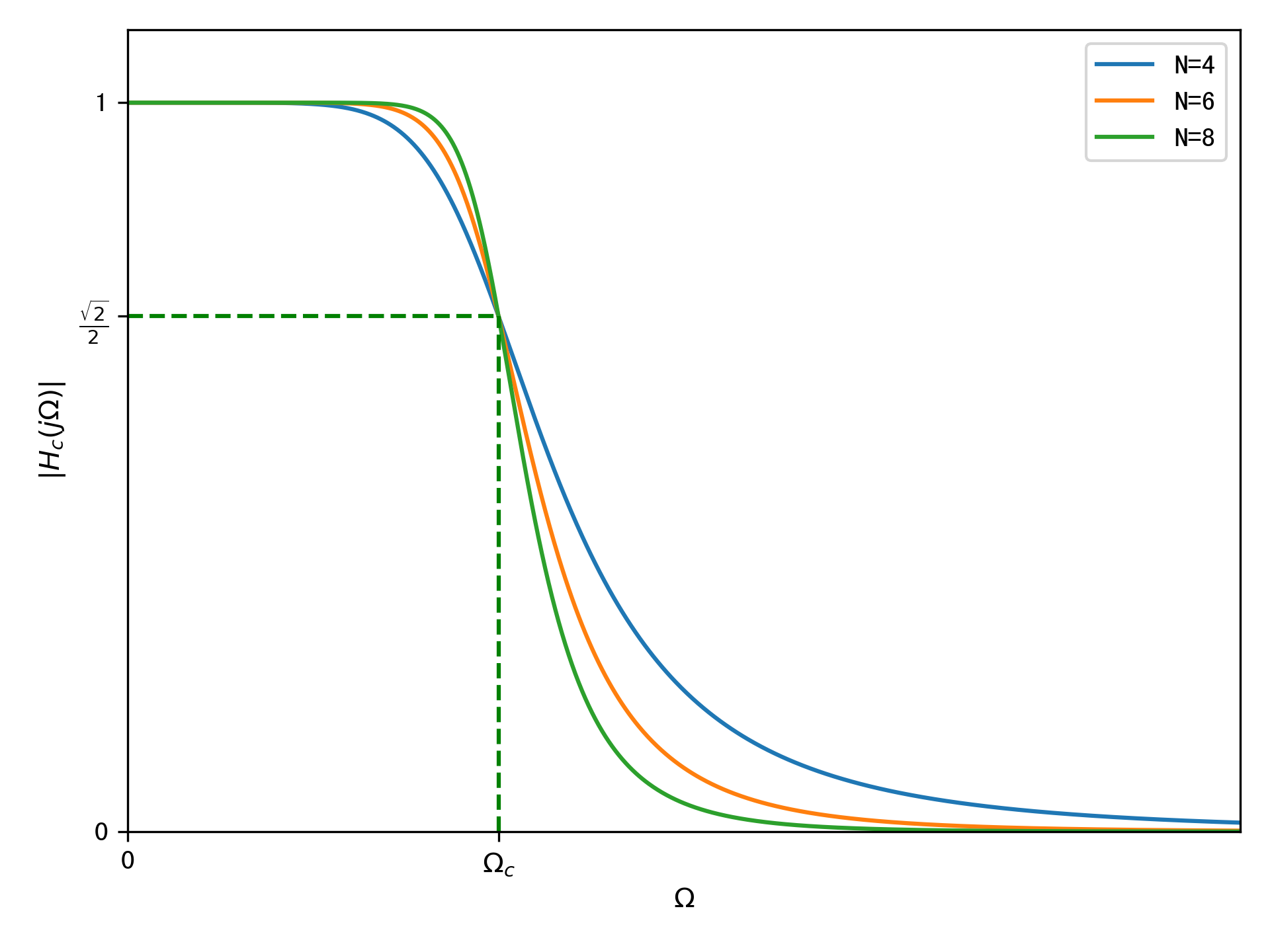
通带内,幅度响应是最大平坦的,对于\(N\)阶的滤波器,意味着幅度平方函数的\(2N-1\)阶导数在\(\Omega=0\)处的值为0。
幅度函数在通带和阻带都是单调递减的。
巴特沃斯滤波器是全极点滤波器。
当\(\Omega=0\)时,幅度函数的值为1。
当\(\Omega=\Omega_c\)时,幅度函数的值为\(\frac{\sqrt{2}}{2}\)。无论滤波器的阶次\(N\)为多少,曲线都要经过3dB这个点。
当\(\Omega < \Omega_c\)时,随着N的增大,通带内的幅度衰减越来越慢。当\(\Omega > \Omega_c\)时,随着N的增大,阻带内的幅度衰减越来越快。
代替\(s=j\Omega\)到幅度平方函数得到:
\(\displaystyle |H_c(s)|^2 = H_c(s)H_c^{\ast}(s) = \frac{1}{1 + \left(\frac{s}{j\Omega_c}\right)^{2N}}\)
由于模拟滤波器的单位脉冲响应是实函数,因此其系统函数\(H(s)\)是共轭对称的,即\(H_c(s)=H_c^{\ast}(-s)\),所以:
\(\displaystyle |H_c(s)|^2=H_c(s)H_c(-s)= \frac{1}{1 + \left(\frac{s}{j\Omega_c}\right)^{2N}}\)
令\(1 + \left(\frac{s}{j\Omega_c}\right)^{2N}=0\)可以得到幅度平方函数的极点如下:
\(\displaystyle s_k = \Omega_c e^{j\frac{(2k+N+1)\pi}{2N}}, k=0,1,\cdots,2N-1\)
极点在s平面是象限对称的(关于虚轴对称,也关于实轴对称),分布在半径为\(\Omega_c\)的圆上,共有\(2N\)个极点。
极点间的角度间隔为\(\frac{\pi}{N}\)。
极点绝对不会落在虚轴上,否则滤波器将是不稳定的。
\(N\)为奇数时,实轴上有极点;\(N\)为偶数时,实轴上没有极点。
下面以\(N=3\)和\(N=4\)为例,画出巴特沃斯幅度平方函数的极点分布图。
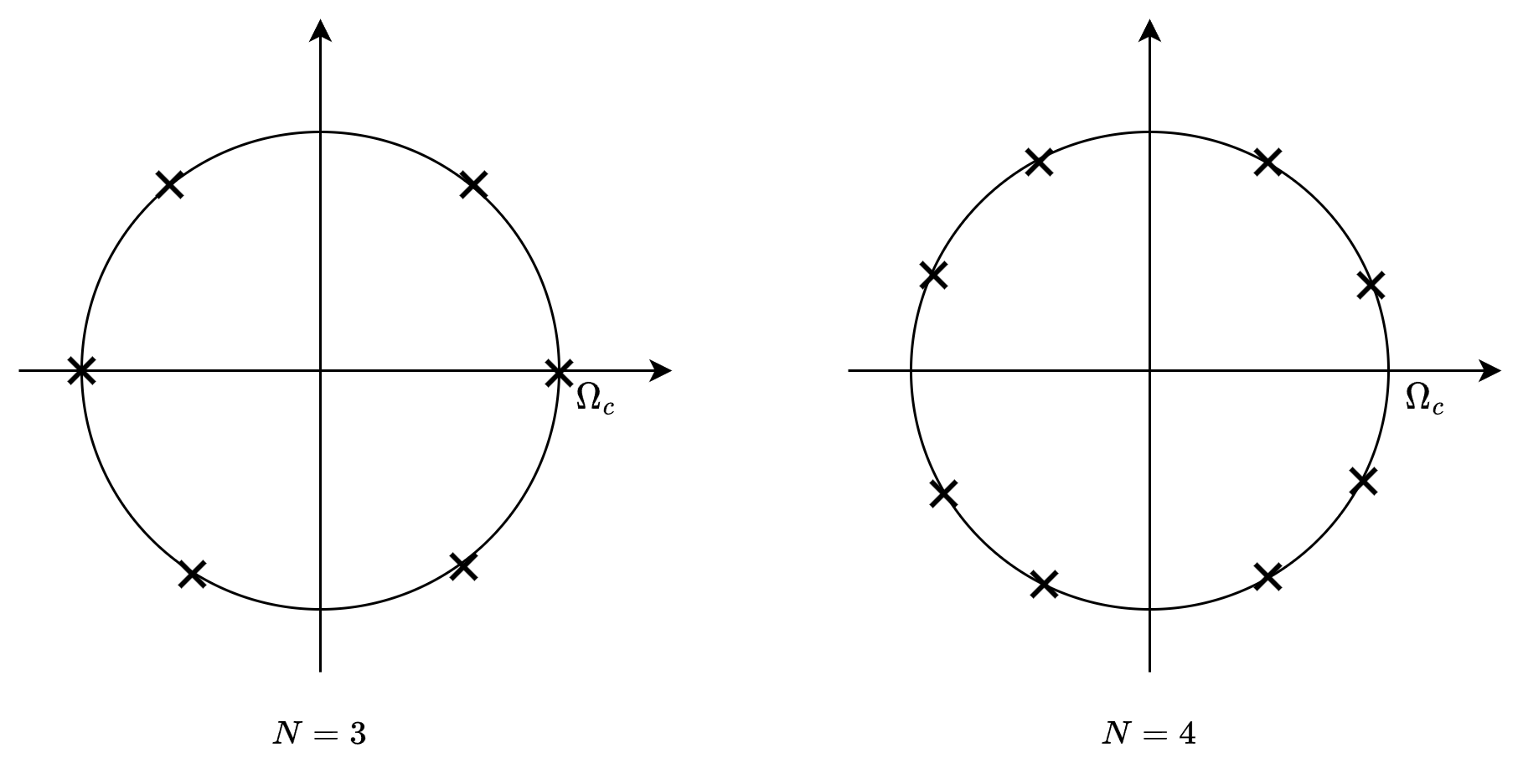
为了保证所设计的系统是因果稳定的,\(H_c(s)\)的极点为幅度平方函数左半平面的极点,因而
\(\displaystyle H_c(s)=\frac{\Omega_c^N}{\prod_{k=0}^{N-1}(s-s_k)}\)
这里的分子系数\(\Omega_c^N\)是由\(H_c(s)\)的低频特性决定的(\(H_c(0)=1\))。
在一般设计中,通常选择\(\Omega_c=1\),这样使频率得到归一化。归一化后,巴特沃斯滤波器的极点分布、系统函数以及分母多项式的系数都有现成的表格可查。
切比雪夫低通滤波器
巴特沃斯低通滤波器通带和阻带都是单调下降的,对于有些滤波器来说,给定一个波动范围,可以允许通带和阻带在这个范围内波动。这样设计出来的滤波器阶次会更低。
切比雪夫I型,通带内有波纹,阻带内是单调下降的。其幅度平方函数表示如下:
\(\displaystyle |H_c(j\Omega)|^2 = \frac{1}{1 +\varepsilon^2V_N^2\left(\frac{\Omega}{\Omega_c}\right)}\)
其中,\(\varepsilon<1\)表示通带波纹大小的一个参数,\(\varepsilon\)越大,波纹也越大,\(N\)为滤波器的阶数。\(V_N(x)\)为\(N\)阶切比雪夫多项式。切比雪夫I型低通滤波器的幅度响应如下:
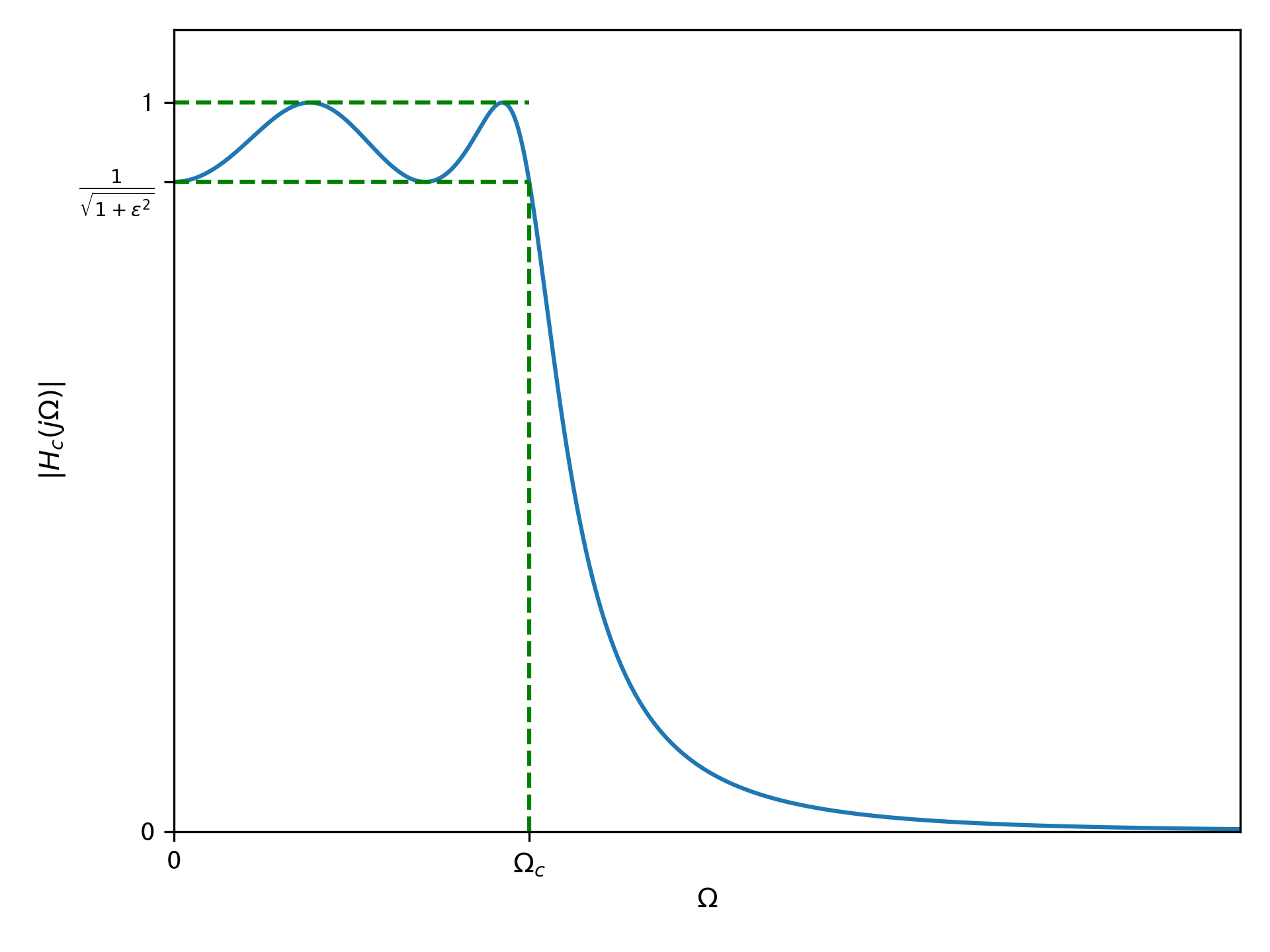
切比雪夫II型,通带内单调下降,阻带内有波纹。其幅度平方函数如下:
\(\displaystyle |H_c(j\Omega)|^2 = \frac{1}{1 +[\varepsilon^2V_N^2\left(\frac{\Omega_c}{\Omega}\right)]^{-1}}\)
切比雪夫II型低通滤波器的幅度响应如下:
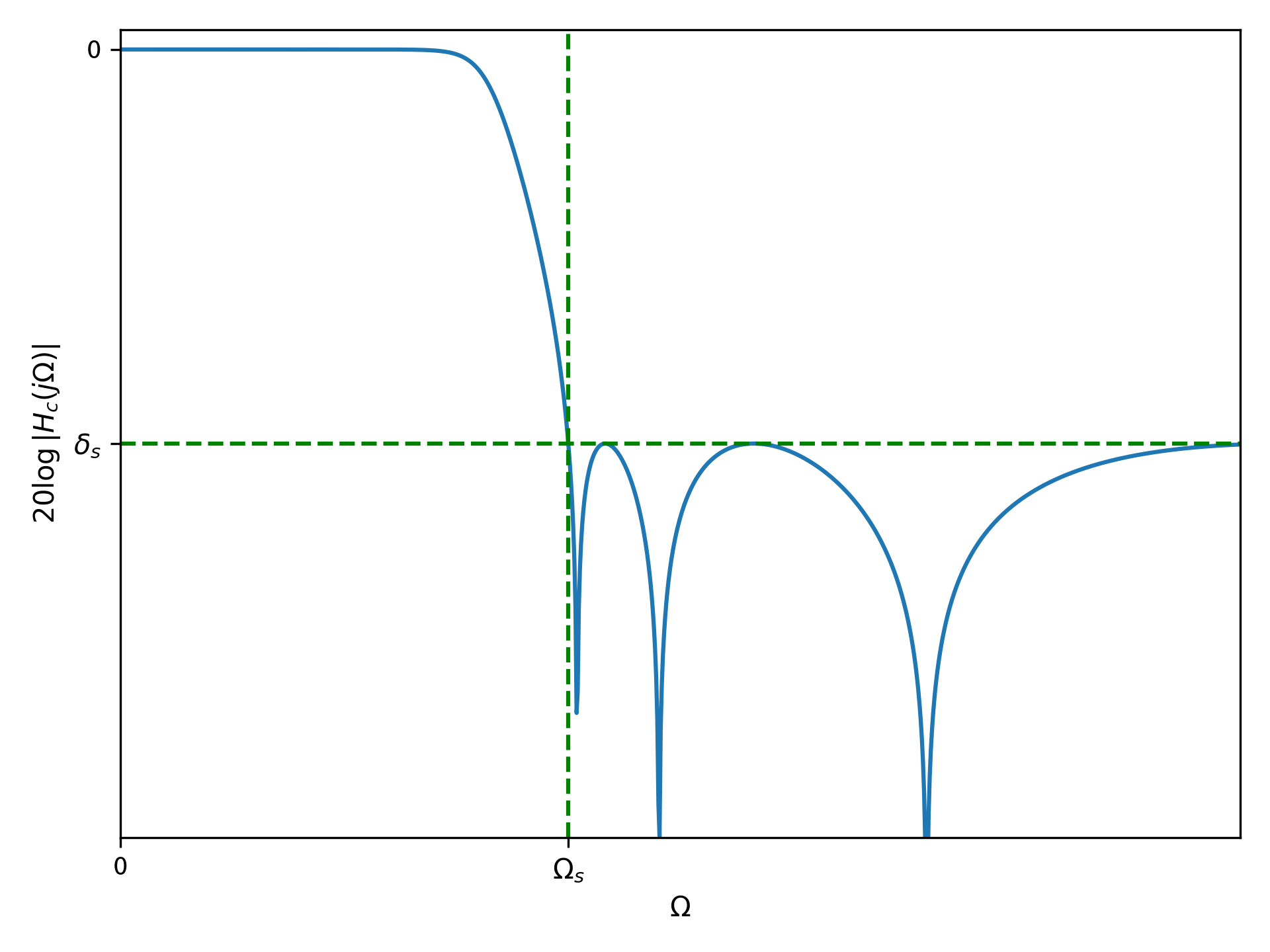
椭圆型滤波器(Elliptic filter)
椭圆型滤波器是在通带和阻带都有波纹的一种滤波器。其幅度平方函数为:
\(\displaystyle |H_c(j\Omega)|^2 = \frac{1}{1 +\varepsilon^2U_N^2\left(\Omega\right)}\)
其中,\(\varepsilon\)表示波纹的大小,\(U_N(x)\)为\(N\)阶雅可比椭圆函数(Jacobian elliptic function)。下图为椭圆型滤波器的幅度响应:
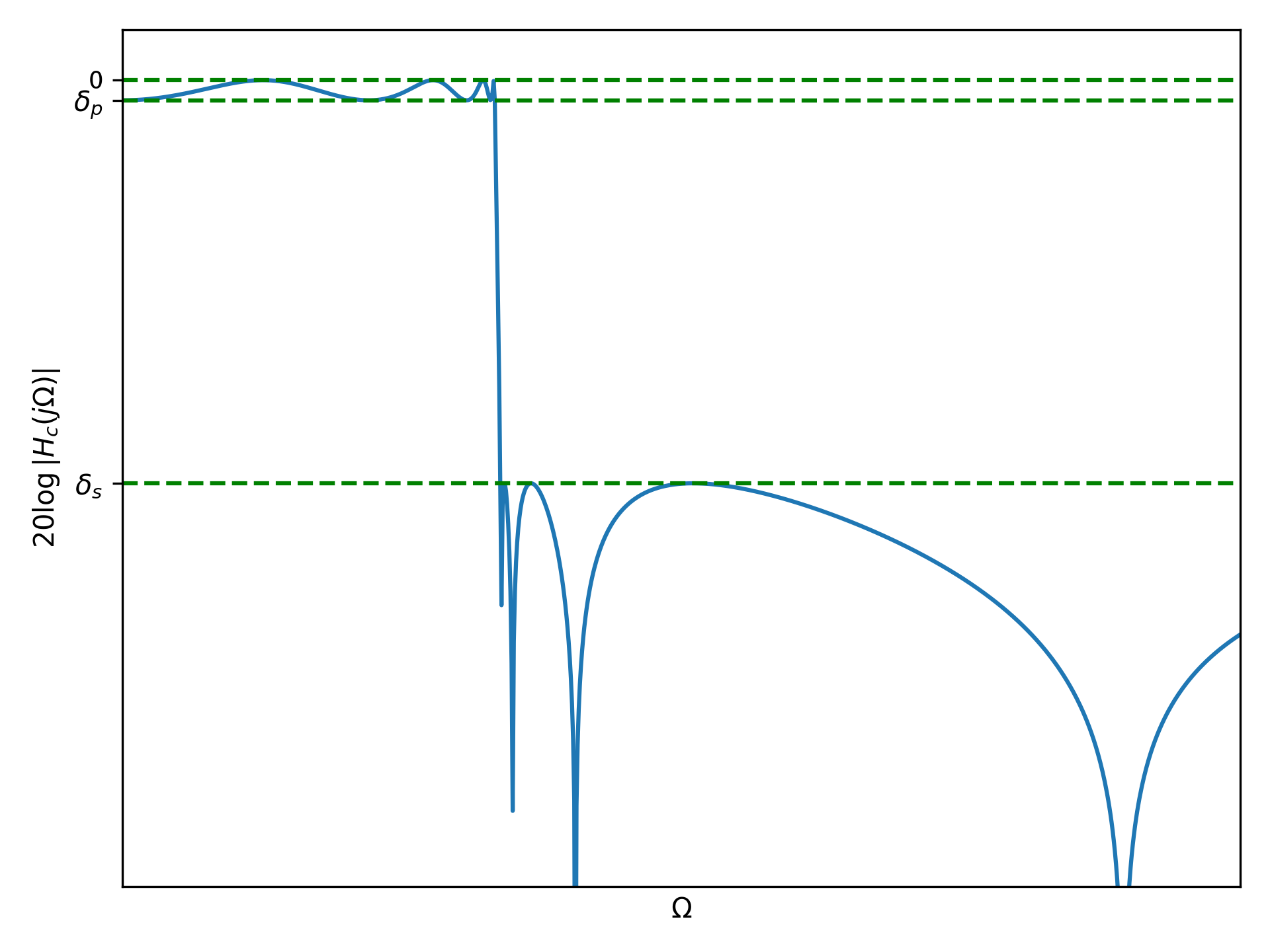
从图中可以看出,椭圆型滤波器的过渡带宽比较窄。
例:用以上四种逼近函数设计一个模拟低通滤波器,通带截止频率为50Hz,阻带截止频率为80Hz,通带最小增益为\(-3dB\),阻带最大增益为\(-60dB\)。
以下为四种逼近函数的设计结果:
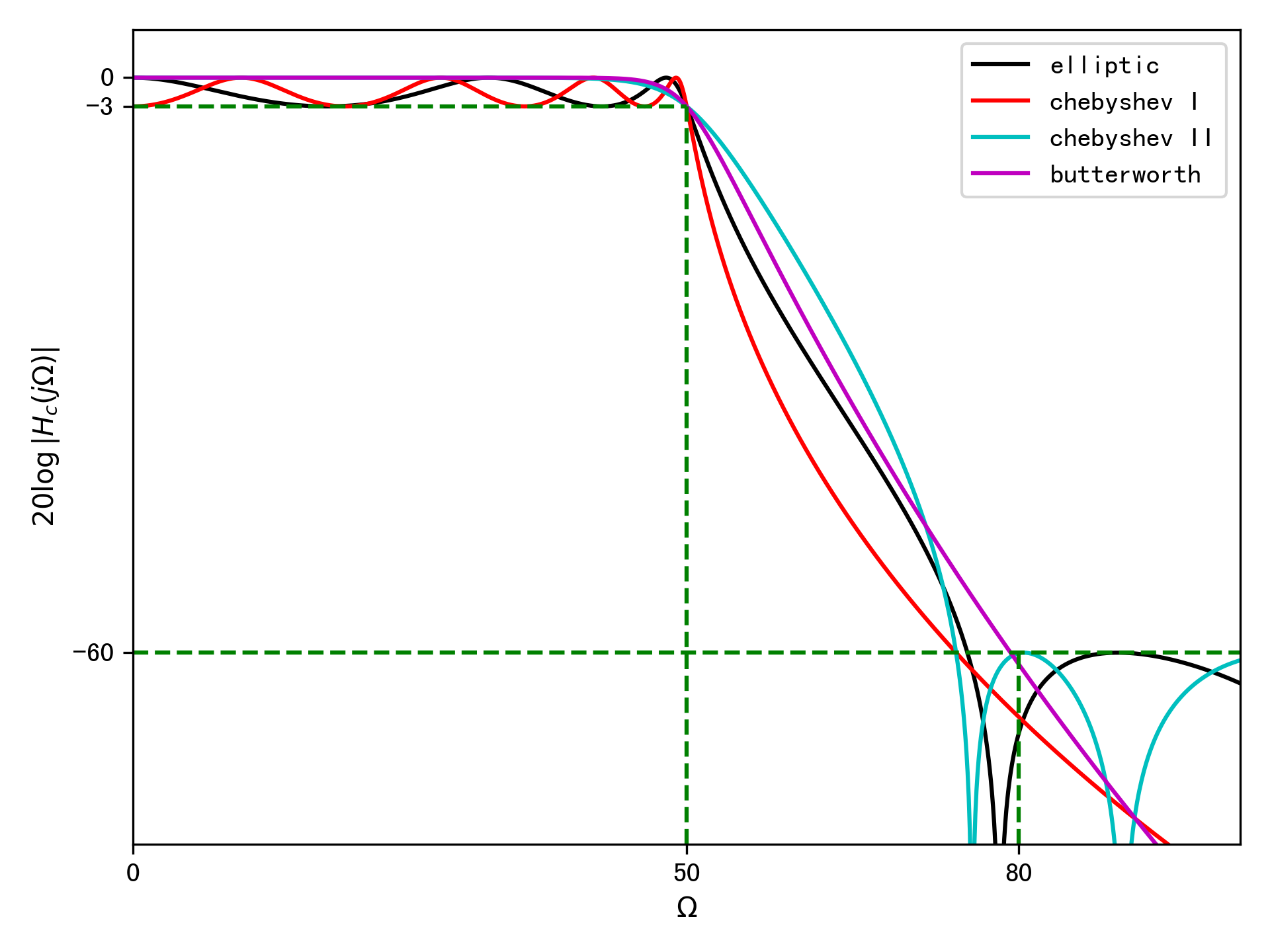
巴特沃斯滤波器所需要的阶次为15,它在通带和阻带内都是单调下降的。
切比雪夫I型滤波器所需要的阶次为8,它在通带内有波纹,阻带内是单调下降的。
切比雪夫II型滤波器所需要的阶次为8,它在通带内是单调下降的,阻带内有波纹。
椭圆型滤波器所需要的阶次为5,它在通带和阻带内都有波纹。