#! https://zhuanlan.zhihu.com/p/667295294

数字滤波器设计

滤波器的定义以及分类

数字滤波器，在这一章中也称之为频率选择性数字滤波器，是一种离散时间系统，其作用是通过输入信号中感兴趣的某一段频率，而抑制不感兴趣的频率。

频率选择性数字滤波器根据幅度响应通常分为低通，高通，带通，带阻，全通数字滤波器。

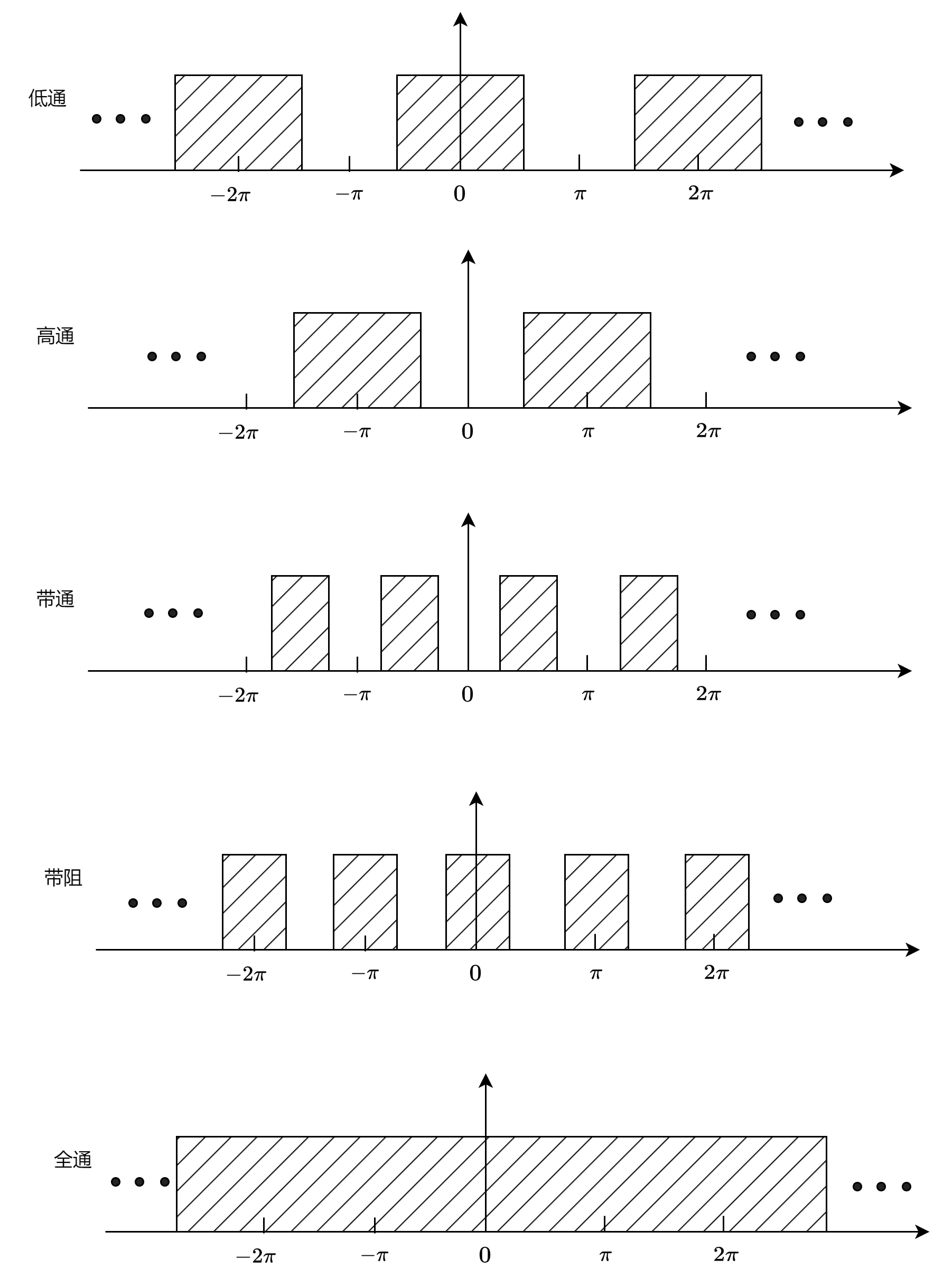
数字滤波器是一个离散时间系统，因此其频域可以用离散时间傅里叶变换(DTFT)来表示。
数字滤波器频率响应是周期的，周期为\(2\pi\)。
对于数字滤波器来说 \(\pi\)的位置是折叠频率的位置，因此高频部分靠近\(\pi\)，低频部分靠近\(0\)。
数字滤波器的单位抽样响应为实数，其频率响应是共轭对称的，因此我们只需要关注\(0\)到\(\pi\)的频率响应即可。

数字滤波器根据其单位抽样响应的长度分为无限长单位抽样响应(IIR)和有限长单位抽样响应(FIR)两类。

IIR滤波器具有如下特点：

系统的单位抽样响应\(h[n]\)是无限长的；
系统函数\(H(z)=\frac{\sum_{k=0}^{M}b_kz^{-k}}{1-\sum_{k=1}^{N}a_kz^{-k}}\)。系统函数中有分母的存在，因此必定有极点的存在，在系统中要避免不稳定的问题；
IIR滤波器难以实现线性相位的特性。

FIR滤波器具有如下特点：

系统的单位抽样响应\(h[n]\)是有限长的；
系统函数\(H(z)=\sum_{k=0}^{M}b_kz^{-k}\)。系统函数中没有分母，因此没有极点的存在，系统是稳定的。
FIR滤波器满足一定约束条件下，可以很容易实现线性相位的特性。

滤波器的设计

在频率选择性数字滤波器中，我们重点研究低通数字滤波器，因为其他的数字滤波器都可以通过低通数字滤波器演变来实现。理想的数字低通滤波器的幅度响应如下图所示：

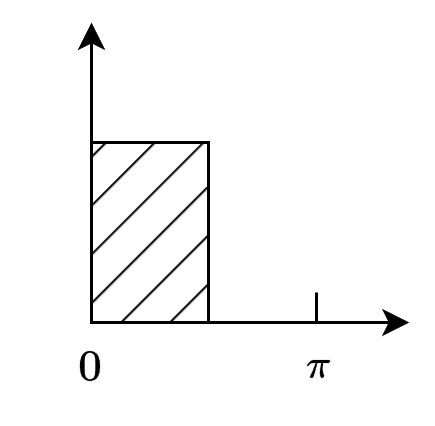
在实际数字滤波器设计中，像上图展示的理想的矩形(brick-wall)滤波器是不可实现的。

实际中的数字滤波器通常用如下示意图来表示：

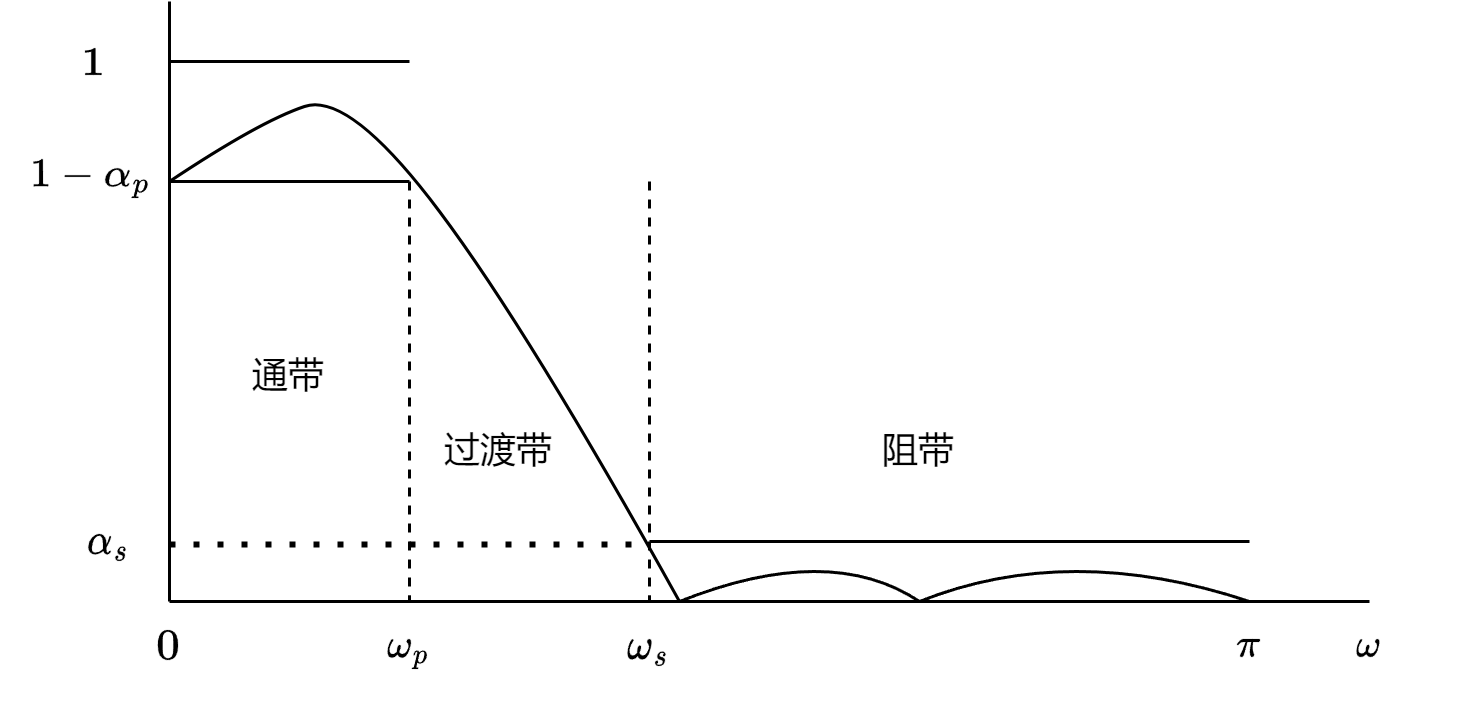
实际的低通数字滤波器由三个部分组成：通带，过渡带，阻带。我们定义\(\omega_p\)和\(\omega_s\)分别为通带截至频率和阻带截至频率，通带内幅度增益在\((1, 1-\alpha_p)\)之间波动，阻带内幅度增益在\((0, \alpha_s)\)之间。过渡带的宽度为\(\omega_s-\omega_p\)。通常我们用分贝来表示通带和阻带内的衰减，即：

通带允许的最大衰减： \(\delta_p = -20\log_{10}(1-\alpha_p)\)

阻带应达到的最小衰减： \(\delta_s = -20\log_{10}(\alpha_s)\)

假设通带允许的最大衰减为\(3dB\)，则幅度增益为\(0.707\)，阻带应达到的最小衰减为\(60dB\)，则幅度增益为\(0.001\)。

频率选择性数字滤波器的设计只考虑了幅度响应的约束，关于相位响应的约束，对于IIR滤波器来说只是系统的因果性和稳定性隐含的施加了极点必须在单位圆内的约束，对于FIR滤波器来说，通常施加了线性相位的约束。因此在频率选择性的数字滤波器设计中，我们只要考虑幅度响应即可。

滤波器的设计就是确定系统函数或常系数差分方程参数的过程。一般包括如下的步骤：

确定滤波器的性能要求；
用因果稳定的线性时不变离散系统去逼近这一性能要求；
系统的实现。

像之前说的，滤波器分为IIR滤波器和FIR滤波器。两类滤波器的设计方法是不同的。IIR滤波器的设计主要是借助于成熟的，有公式借鉴的连续模拟滤波器的设计方法，然后再利用冲激响应不变法或者双线性变换法将模拟滤波器转换为数字滤波器。FIR滤波器的设计主要是基于窗函数法和最优化法等。

接下来我们先讲讲模拟滤波器的设计方法，请参考模拟滤波器设计的章节。