#! https://zhuanlan.zhihu.com/p/666067595
离散时间系统的结构
离散时间系统可以由表示输入和输出关系的常系数线性差分方程、系统的单位抽样响应或系统函数来表征。给定一个常系数的线性差分方程如下:
\(\displaystyle y[n]=\sum_{k=1}^{N}a_ky[n-k]+\sum_{k=0}^{M}b_kx[n-k]\)
信号进入该系统,相当于该系统把输入序列通过上面的运算变换成输出序列。可以通过在软件上编程或通过设计专门的数字电路实现上述的过程。我们可以看到由常系数线性差分方程描述的系统可以用加法器、乘法器和单位延迟基本操作相互连接而成的结构来表示。这些基本的单元可以用信号流图法表示如下:
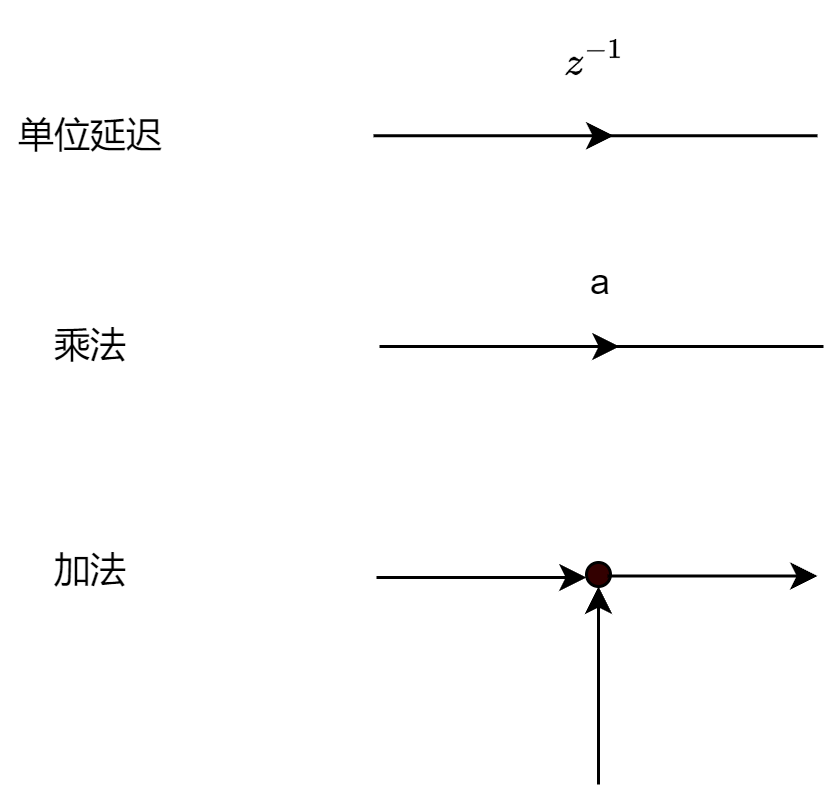
给定一个二阶离散时间系统,其差分方程为:
\(\displaystyle y[n]=a_1y[n-1]+a_2y[n-2]+b_0x[n]\)
其信号流图法表示如下:
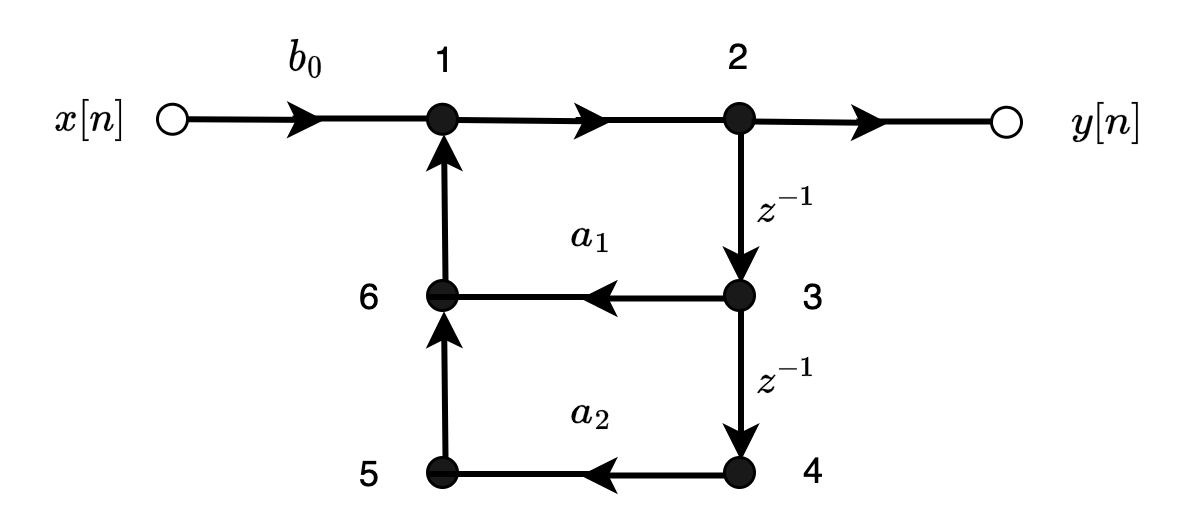
从图中可以看出1、6这种节点属于加法器,它有两个输入一个输出,2、3、4、5这种节点属于分支节点,它有一个输入,一个或者两个输出,对于加法器,输出是等于输入的和,对于分支节点,输入和输出的节点值都是相等的。
图中的运算结构是重要的,不同的结构所需要的硬件资源(存储单元,乘法器和加法器)是不同的,因此在实际的应用中,我们需要选择合适的结构来实现离散时间系统。另外,在有限精度(有限字长)情况下,不同的运算结构的误差和稳定性是不同的。
由于无限长单位冲激响应系统与有限长单位冲激响应系统在结构上各有不同的特点,我们接下来分别讨论了这两种系统的结构。
单位延迟相当于存储器,信号经过一个单位延迟,相当于把上一时刻的数据存储到存储器中。因此单位延迟多的话,所需要的存储器就越多。
IIR系统的基本结构
直接I型结构
给定一常系数的线性差分方程如下:
\(\displaystyle y[n]=\sum_{k=1}^{N}a_ky[n-k]+\sum_{k=0}^{M}b_kx[n-k]\)
其系统函数为:
\(\displaystyle H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^{M}b_kz^{-k}}{1-\sum_{k=1}^{N}a_kz^{-k}}\)
直接I型结构的信号流图如下:
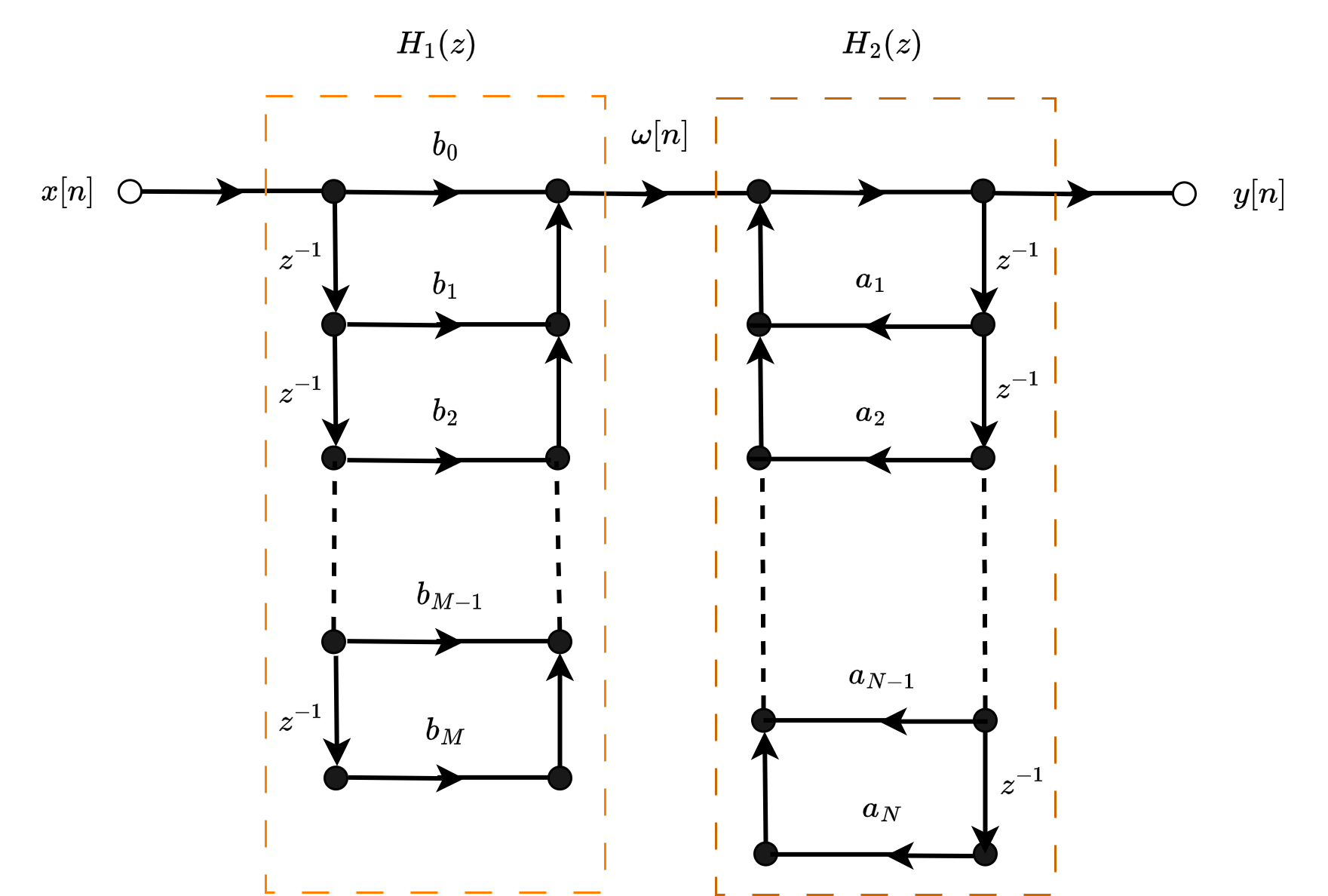
从图中可以看出直接I型需要\(N+M\)个单位延迟。
直接II型结构(典范性)
调换一下\(H_1(z)\)和\(H_2(z)\)的位置,除了中间结果有所变化外,\(y[n]\)与\(x[n]\)的关系没有变化,我们可以得到直接II型结构的信号流图如下:
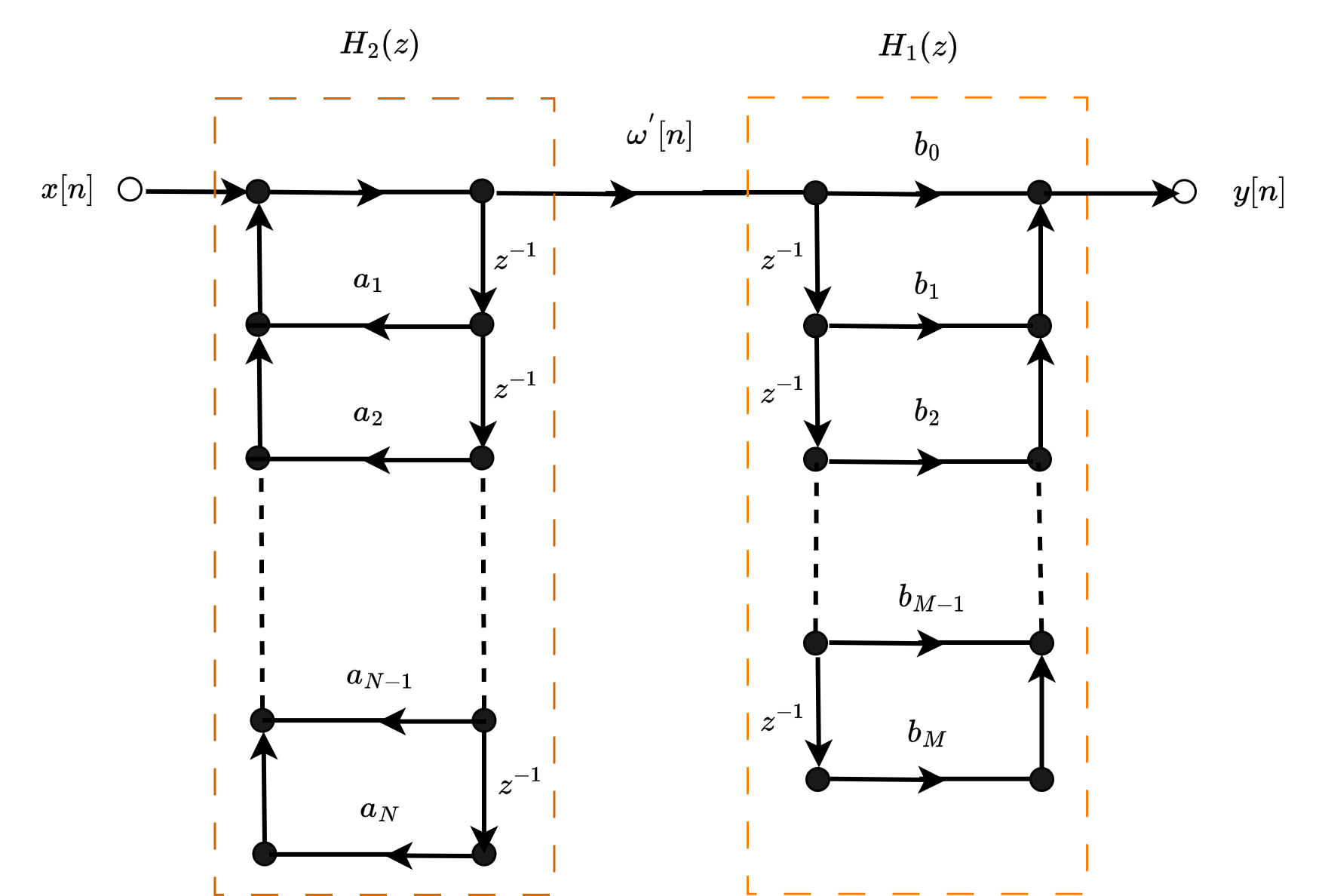
将中间的单位延迟合并,可以得到下面的信号流图:
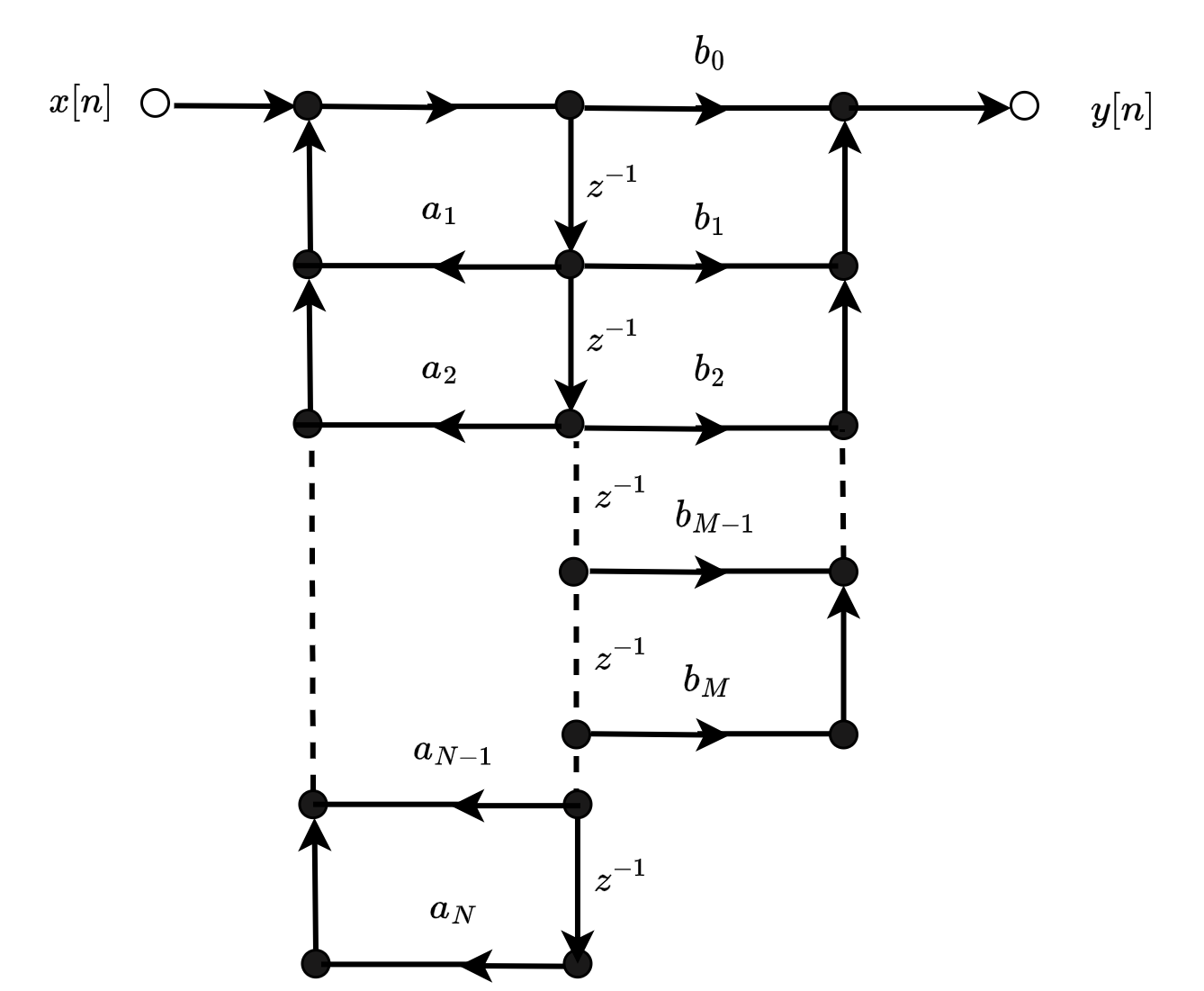
从图中可以看出延迟单元减少到了\(N\)个,通常\(N>M\)。
在采用定点计算的高阶IIR系统中,由于有限字长效应的影响,会引起极点的位置变化,直接I型和II型结构无法有效地控制极点和零点,因此很少采用这两种结构。
级联结构
级联结构是一种常用的结构,它可以有效地控制极点和零点的位置,从而减少有限字长效应的影响。
给定一系统函数,我们对其分子和分母进行因式分解,可以得到:
\(\displaystyle H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{k=0}^{M}b_kz^{-k}}{1-\sum_{k=1}^{N}a_kz^{-k}}=A\frac{\prod_{k=1}^{M_1}(1-p_kz^{-1})\prod_{k=1}^{M_2}(1-q_kz^{-1})(1-q_k^*z^{-1})}{\prod_{k=1}^{N_1}(1-c_kz^{-1})\prod_{k=1}^{N_2}(1-d_kz^{-1})(1-d_k^*z^{-1})}\)
式中\(M=M_1+2M_2\),\(N=N_1+2N_2\)。一阶因式表示实根,\(p_k\)为实零点,\(c_k\)为实极点。二阶因式表示复共轭根,\(q_k\)和\(q_k^*\)是共轭零点,\(d_k\)和\(d_k^*\)是共轭极点,A为实数。
把共轭因子组合成实系数的二阶因子,并将实系数的一阶因子组合成二阶因子,则整个网络可以组合成一系列二阶因子的级联结构(如果\(N\)和\(M\)为奇数的话,最后级联的是一阶因子)。
\(\displaystyle H(z)=A\prod_{k}\frac{1+b_{1k}z^{-1}+b_{2k}z^{-2}}{1-a_{1k}z^{-1}-a_{2k}z^{-2}} = A \prod_{k}H_{k}(z)\)
以6阶系统为例,如果用级联的形式表示如下:
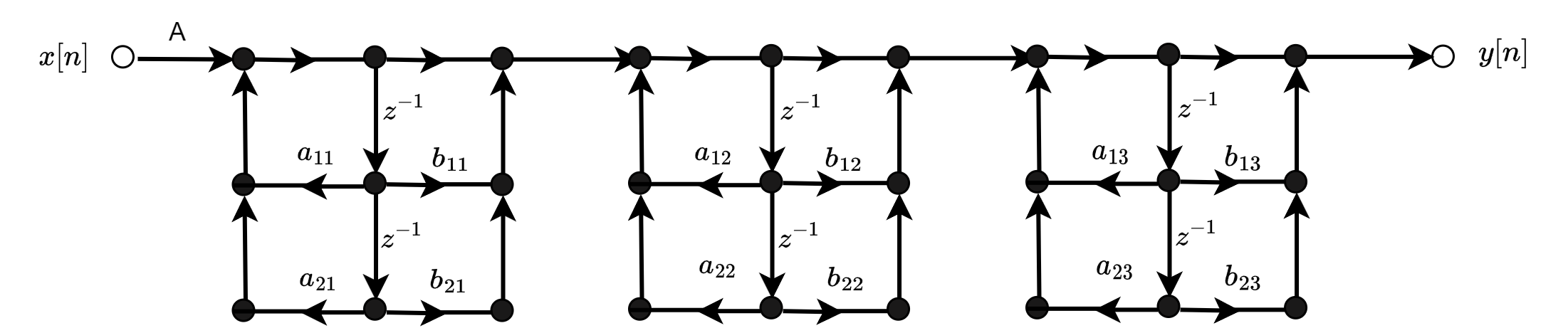
其中\(b_{1k}\)和\(b_{2k}\)能够单独调整第k个零点,而不影响其他的零极点。\(a_{1k}\)和\(a_{2k}\)可以单独调整第k个极点,而不影响其他的零极点。因此级联结构可以有效地控制极点和零点的位置,从而减小有限字长效应的影响。在定点运算的高阶IIR系统中经常采用。
级联系统会引起计算误差的传播,二阶因子组成的二阶基本节有多种组合方式,可以通过计算机仿真找到最优组合。
并联结构
我们将系统函数按如下的方式分解,就得到了并联型结构:
\(\displaystyle H(z)=\frac{Y(z)}{X(z)}=\sum_{k=0}^{N_p}C_kz^{-k}+\sum_{k=1}^{N_1}\frac{A_k}{1-c_kz^{-1}}+\sum_{k=1}^{N_2}\frac{B_k(1-e_k z^{-1})}{(1-d_kz^{-1})(1-d_k^{\ast}z^{-1})}\)
其中\(N=N_1+2N_2\)。如果\(M \geq N\),则\(N_p=M-N\)。如果\(M < N\),则\(C_k=0\),第一项不存在。我们也可以将一阶的实极点因子组合成二阶因子,于是:
\(\displaystyle H(z)=\sum_{k=0}^{N_p}C_kz^{-k}+\sum_{k=1}^{N_s}\frac{e_{0k}+e_{1k}z^{-1}}{1-a_{1k}z^{-1}-a_{2k}z^{-2}}\)
以6阶系统为例,其中\(M=N=6\),系统的结构如下:
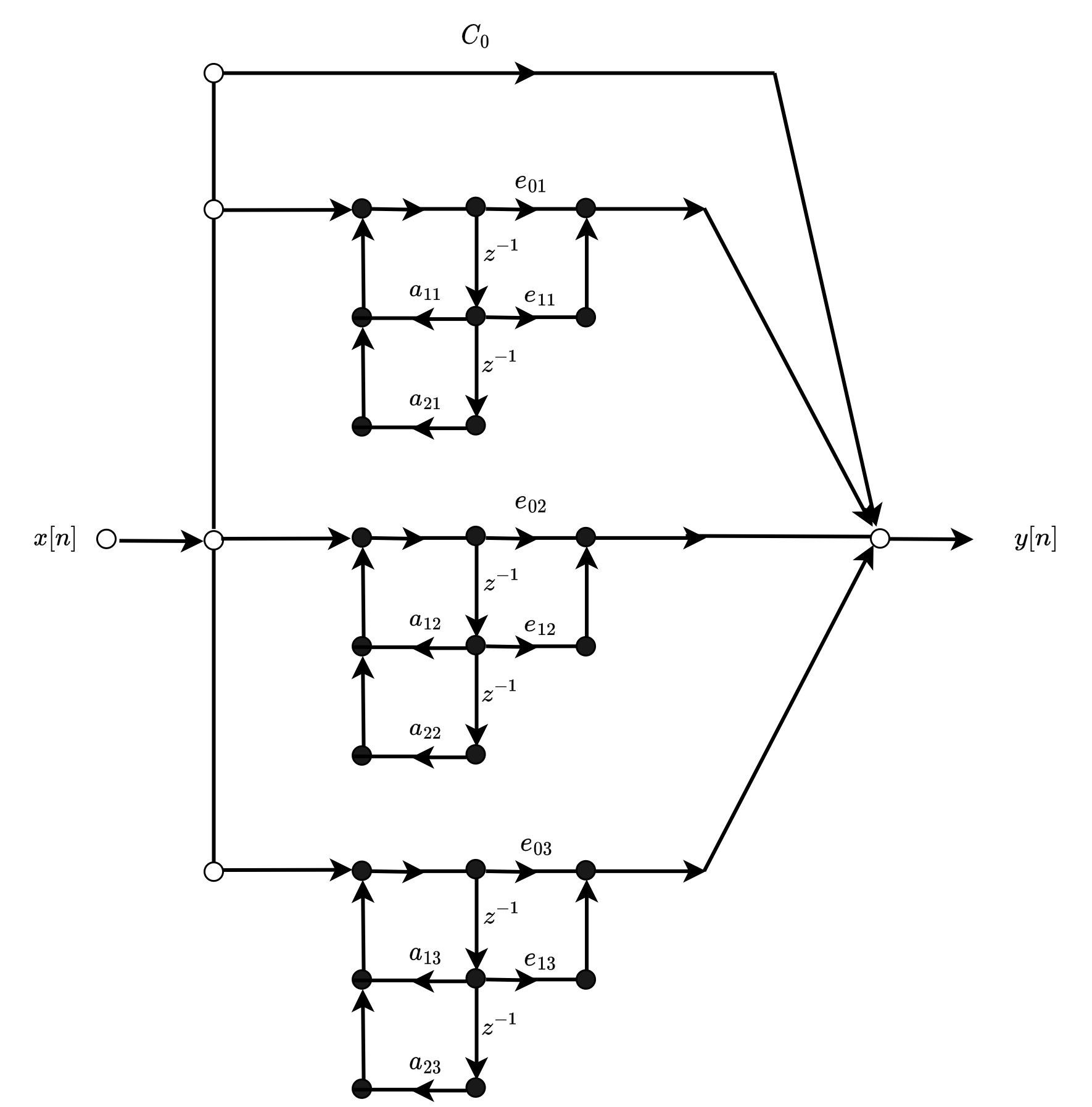
其中\(C_k\)可以单独调整第k个零点,而不影响其他的零极点。\(a_{1k}\)和\(a_{2k}\)可以单独调整第k个极点,但不能调整零点。因此并联结构可以有效地控制极点的位置,但是不能控制零点的位置,且计算误差不会传播,从而计算的误差会比级联结构稍微小点。
转置定理
将线性时不变网络中所有支路方向倒转,所有节点的输入和输出互换,得到的网络与原网络具有相同的输入输出关系,这就是转置定理。转置定理导出的网络结构提供了一种有效的实现方法。下面以典范II型结构为例,说明转置定理的应用。
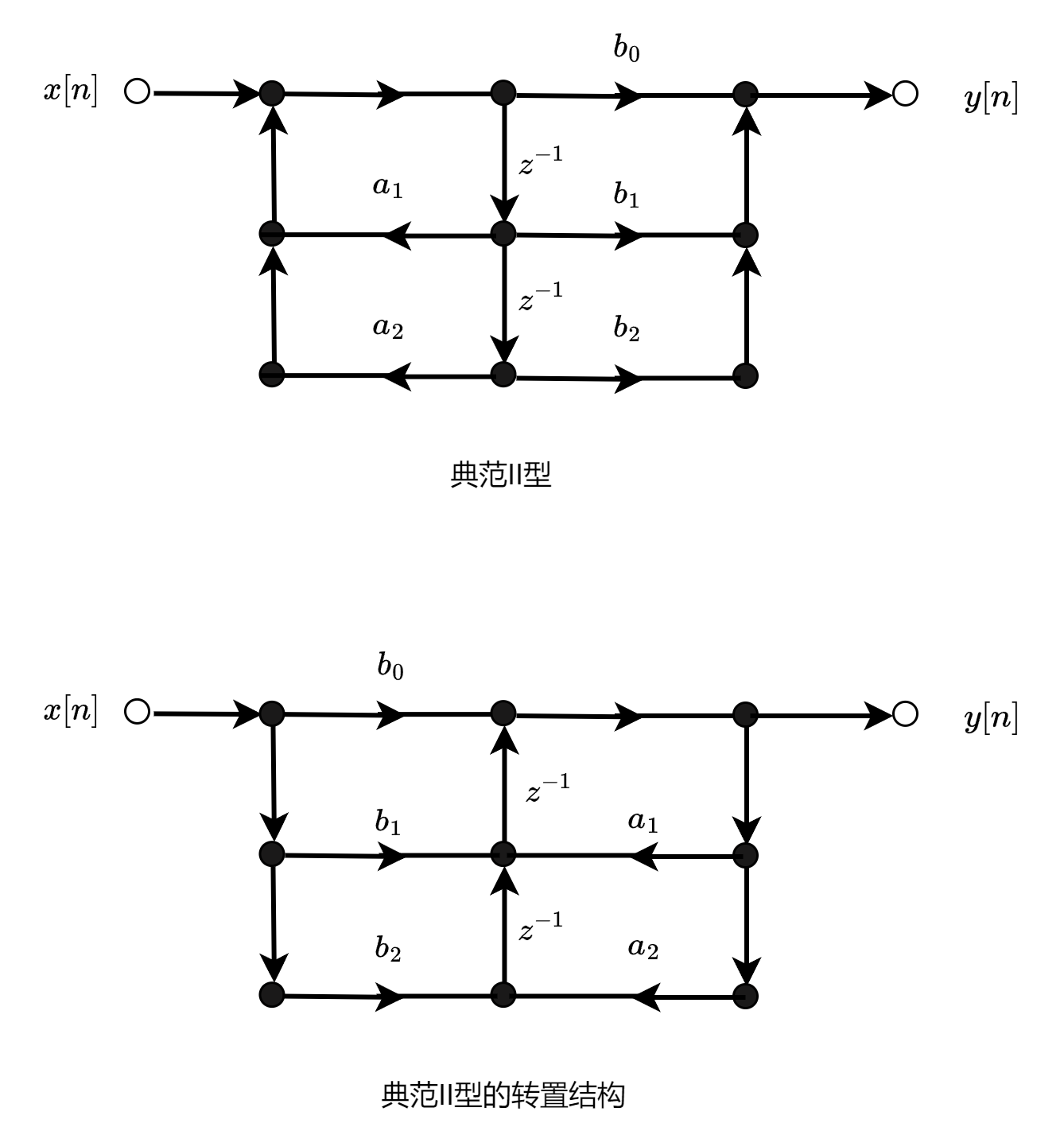
FIR系统的基本结构
直接型结构
对于因果稳定的FIR系统,系统函数在有限的Z平面上只有零点,极点全部在\(z=0\)处,因此FIR系统的常系数线性差分方程表达式如下:
\(\displaystyle y[n]=\sum_{k=0}^{M}b_kx[n-k]\)
系统的输出\(y[n]\)等于系统的输入\(x[n]\)与单位抽样响应\(h[n]\)的卷积。\(h[n]\)表示如下:
\(\displaystyle h[n]=\left\{\begin{array}{ll}b_n, & n=0,1,\cdots,M, \\ 0, & \text{otherwise.}\end{array}\right.\)
因此,FIR系统的直接型结构可以用下面的信号流图表示:

这种结构也称之为抽头延时线结构或横向滤波器结构。
利用转置定理可以得到如下结构:

级联型结构
为了有效地控制零点,我们可以将系统函数表示成:
\(\displaystyle H(z)=\sum_{n=0}^{M}h[n]z^{-n}=\prod_{k=1}^{M_s}(b_{0k}+b_{1k}z^{-1}+b_{2k}z^{-2})\)
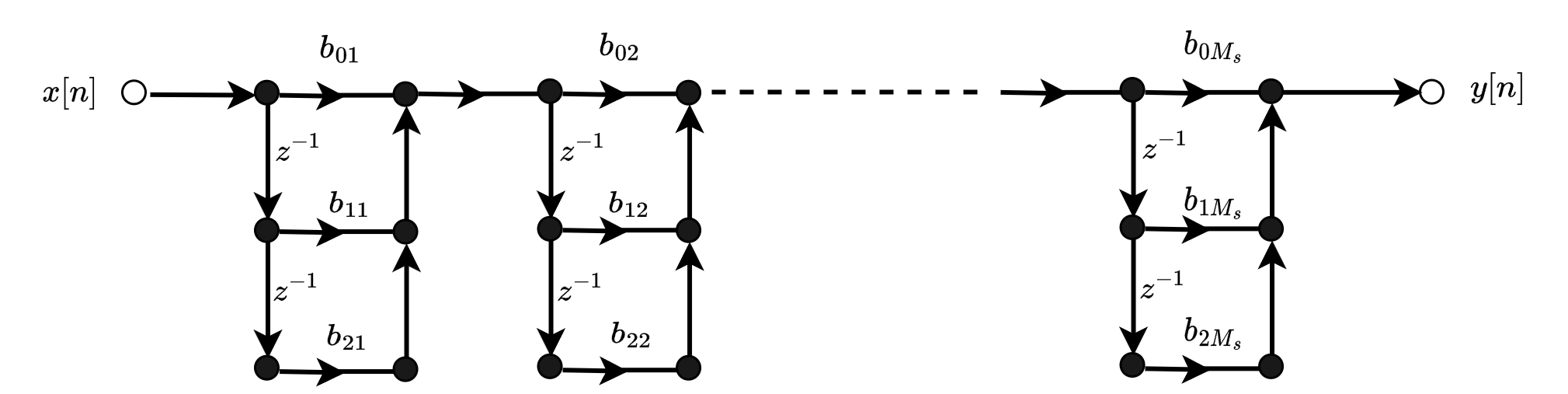
线性相位结构
如果FIR系统是线性相位的系统,则\(h[n]\)是实数,且满足如下条件:
\(\displaystyle h[n]=\pm h[M-n]\)
也就是说对称中心在\(\frac{M}{2}\)处。
当\(M\)为偶数时,系统的结构如下:
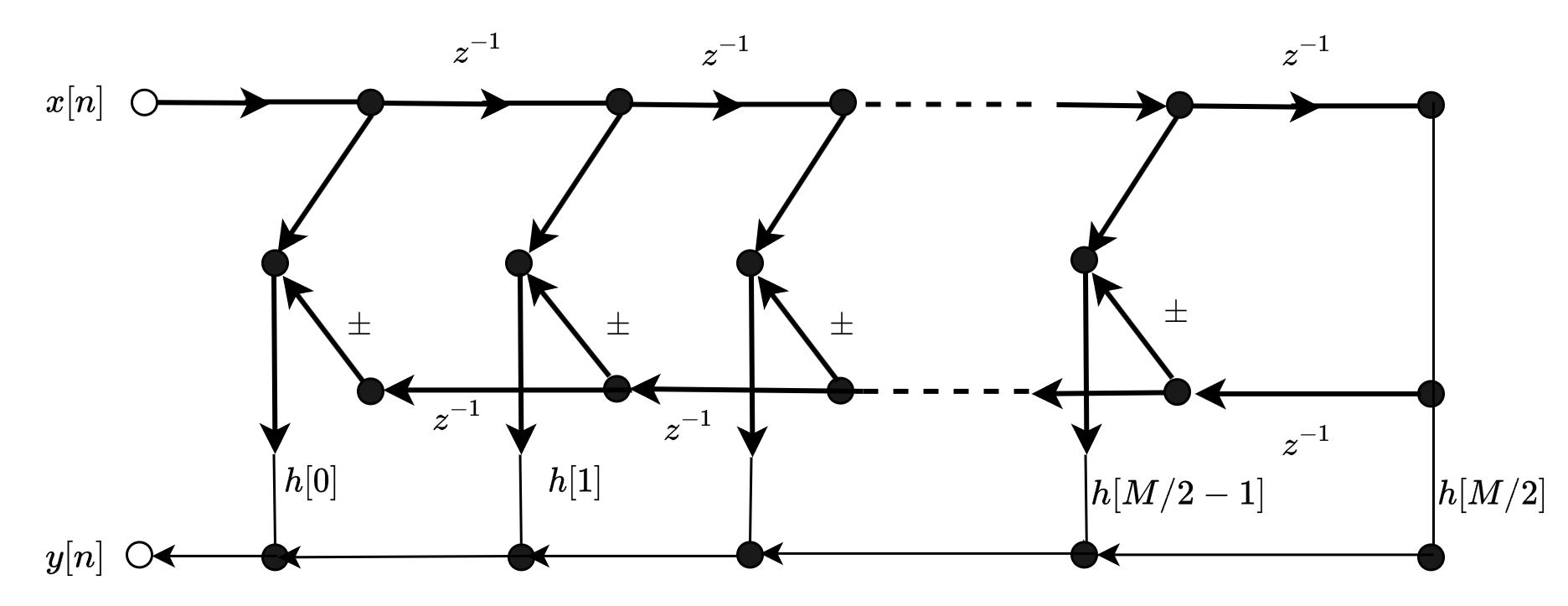
当\(M\)为奇数时,系统的结构如下:
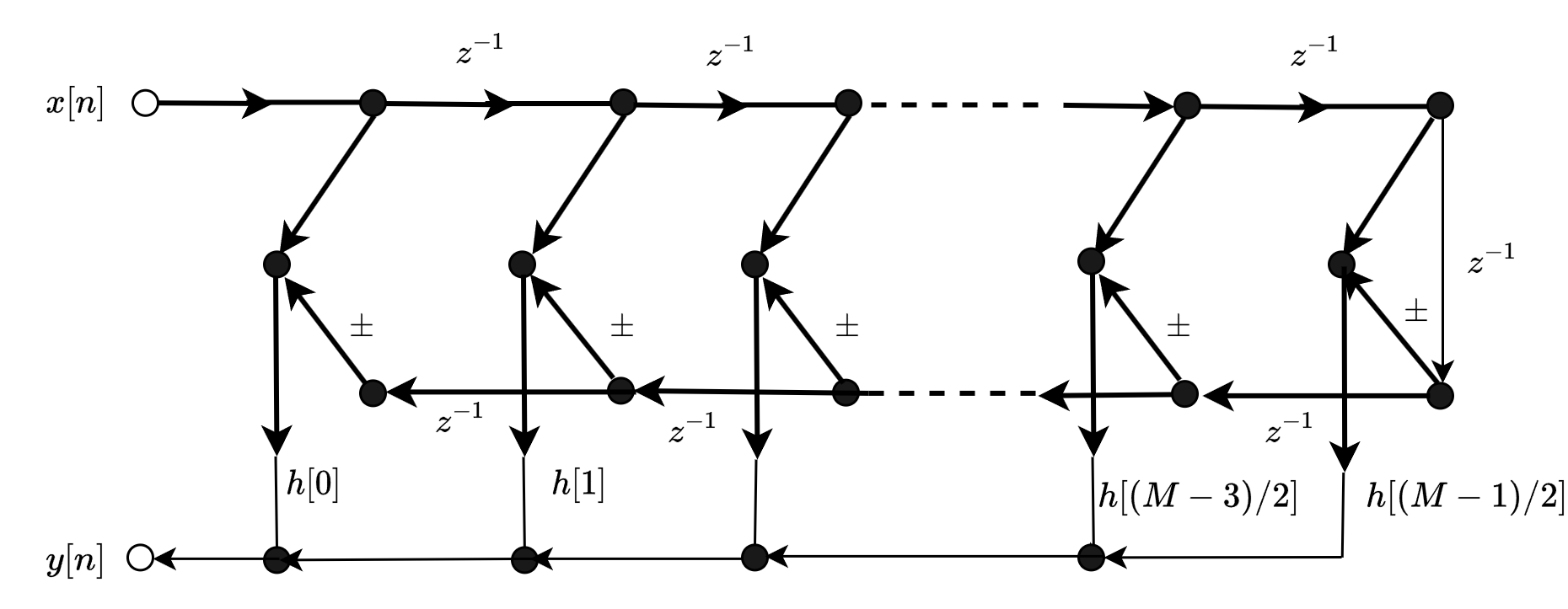
从线性相位的FIR结构可以看出,其中乘法次数比之前的直接型减少了一半。