基本原理
设序列\(x[n]\)的长度为\(N=4^M\),\(M\)为整数。如果不满足这个条件,可以通过补零,使之达到这个要求。我们通过抽取将\(x[n]\)分为四个长度为\(N/4\)的子序列如下:
\(\displaystyle x_1[n] = x[4n]\)
\(\displaystyle x_2[n] = x[4n+1]\)
\(\displaystyle x_3[n] = x[4n+2]\)
\(\displaystyle x_4[n] = x[4n+3]\)
则\(x[n]\)的DFT可以表示为:
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k)& =\sum_{n=0}^{N-1}x[n]W_N^{nk} \\
& = \sum_{n=0}^{N/4-1}x[4n]W_N^{4nk} + \sum_{n=0}^{N/4-1}x[4n+1]W_N^{(4n+1)k} + \sum_{n=0}^{N/4-1}x[4n+2]W_N^{(4n+2)k} + \sum_{n=0}^{N/4-1}x[4n+3]W_N^{(4n+3)k} \\
& = \sum_{n=0}^{N/4-1}x[4n]W_{N/4}^{nk} + \sum_{n=0}^{N/4-1}x[4n+1]W_{N/4}^{nk}W_N^{k} + \sum_{n=0}^{N/4-1}x[4n+2]W_{N/4}^{nk}W_N^{2k} + \sum_{n=0}^{N/4-1}x[4n+3]W_{N/4}^{nk}W_N^{3k} \\
& = \sum_{n=0}^{N/4-1}x_1[n]W_{N/4}^{nk} + \sum_{n=0}^{N/4-1}x_2[n]W_{N/4}^{nk}W_N^{k} + \sum_{n=0}^{N/4-1}x_3[n]W_{N/4}^{nk}W_N^{2k} + \sum_{n=0}^{N/4-1}x_4[n]W_{N/4}^{nk}W_N^{3k} \\
& = X_1(k) + W_N^kX_2(k) + W_N^{2k}X_3(k) + W_N^{3k}X_4(k) \\
\end{split}\end{equation*}\end{split}\]
其中,\(X_1(k)\),\(X_2(k)\),\(X_3(k)\),\(X_4(k)\)分别为\(x_1[n]\),\(x_2[n]\),\(x_3[n]\),\(x_4[n]\)的\(N/4\)点的DFT,\(k=0,1,\cdots,N/4-1\),\(W_N^k\),\(W_N^{2k}\)和\(W_N^{3k}\)为旋转因子。通过上面的公式,我们只计算出来了\(k=0,1,\cdots, N/4-1\)的\(X[k]\)。对于\(k=N/4,N/4+1,\cdots,N-1\),我们可以通过下面的公式计算:
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k+N/4)& = X_1(k) + W_N^{k+N/4}X_2(k) + W_N^{2(k+N/4)}X_3(k) + W_N^{3(k+N/4)}X_4(k) \\
& = X_1(k) -j W_N^kX_2(k) - W_N^{2k}X_3(k) + j W_N^{3k}X_4(k) \end{split}\end{equation*}\end{split}\]
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k+2N/4)& = X_1(k) + W_N^{k+2N/4}X_2(k) + W_N^{2(k+2N/4)}X_3(k) + W_N^{3(k+2N/4)}X_4(k) \\
& = X_1(k) - W_N^kX_2(k) + W_N^{2k}X_3(k) - W_N^{3k}X_4(k) \end{split}\end{equation*}\end{split}\]
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k+3N/4)& = X_1(k) + W_N^{k+3N/4}X_2(k) + W_N^{2(k+3N/4)}X_3(k) + W_N^{3(k+3N/4)}X_4(k) \\
& = X_1(k) +j W_N^kX_2(k) - W_N^{2k}X_3(k) - j W_N^{3k}X_4(k) \end{split}\end{equation*}\end{split}\]
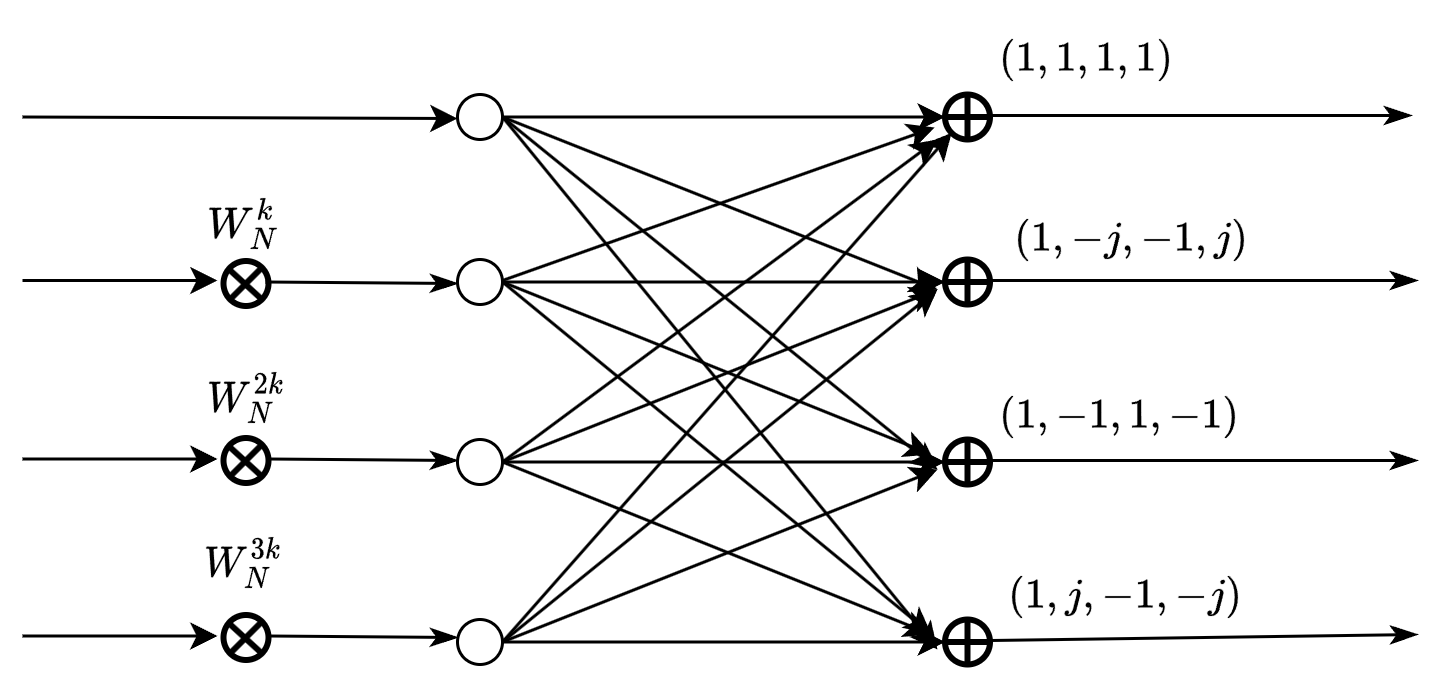
我们可以用下面的示意图表示上述的过程:
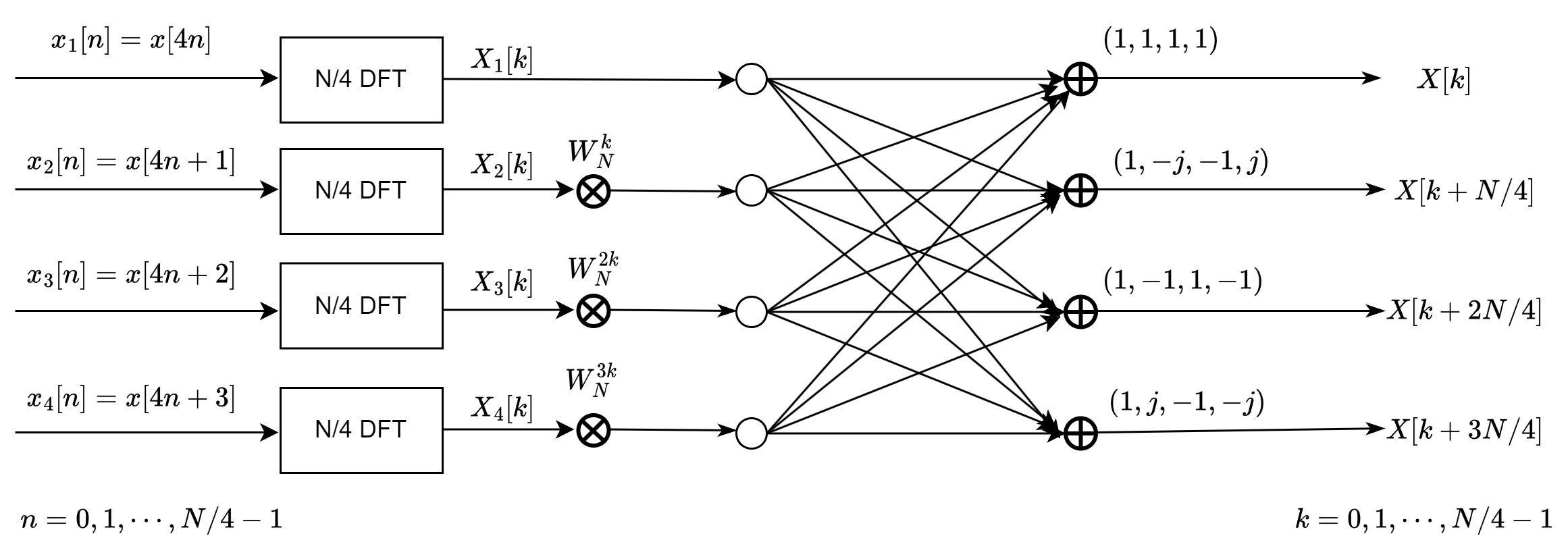
对于序列\(x_1[n]]\),\(x_2[n]]\),\(x_3[n]]\),\(x_4[n]]\),我们可以继续用上述分而治之的方法(divide and conquer)将每个序列分为四个长度为\(N/16\)的子序列,我们画出了\(X_1[n]\)划分的示意图:
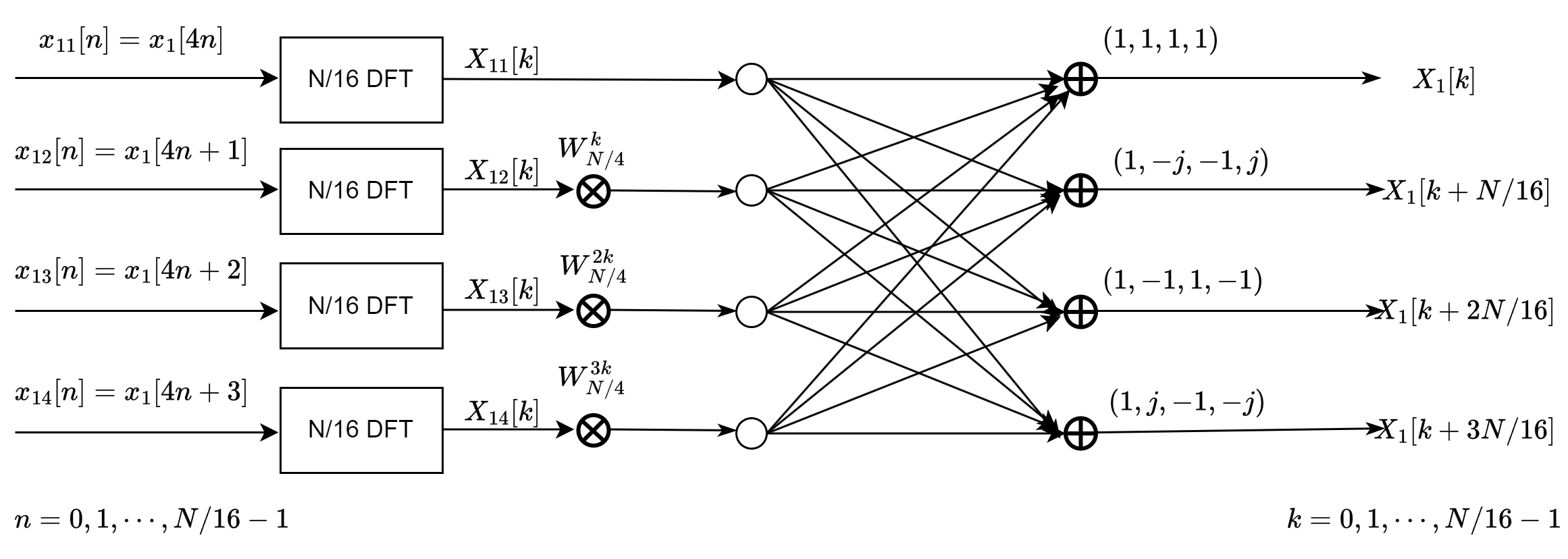
我们可以继续用上述的方法将每个子序列继续划分,直到最后序列长度为4。4点的DFT计算如下:
\[\begin{split}\displaystyle \begin{bmatrix} X[0] \\ X[1] \\
X[2]\\ X[3] \end{bmatrix} =\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & -j & -1 & -j \\
1 & -1 & 1 & -1 \\
1 & j & -1 & j
\end{bmatrix}\cdot \begin{bmatrix} x[0] \\ x[1] \\
x[2]\\ x[3] \end{bmatrix} \end{split}\]