#! https://zhuanlan.zhihu.com/p/657748871
信号
信号是指信息的传递或传输过程中所使用的一种物理量。在数学表示上,信号是一个函数。在本书中,信号是关于时间的一个函数,即\(t\)的函数。信号可以是连续的,也可以是离散的。在本书中,我们主要讨论离散时间信号。
信号的分类
信号可以按照不同的标准进行分类。
根据载体的不同, 信号可以是电的、磁的、声的、光的、机械的、热的等各种信号。
若信号是一个变量的函数,则称为一维信号,若信号是两个变量的函数,则称为二维信号;推而广之,若信号是多个变量的函数,则称为多维信号(即矢量信号)。信号的变量可以是时间、空间或其他的物理量等。
周期信号和非周期信号。周期信号是指在一定时间间隔内,信号的波形是重复的。非周期信号是指在一定时间间隔内,信号的波形是不重复的。
确定信号和随机信号。确定信号是指在任意时刻,信号的值都是确定的。随机信号是指在任意时刻,信号的值是随机的。假定信号\(x(t)=A\cos(2\pi t+\frac{\pi}{3})\),若\(A\)是确定的,则\(x(t)\)是确定信号;若\(A\)以某一概率取值\(1\)或\(-1\)、则\(x(t)\)是随机信号。
功率信号和能量信号。功率信号是指信号的平均功率是有限的。能量信号是指信号的能量是有限的。周期信号和随机信号是功率信号。
连续时间信号(即模拟信号)指的是信号的时间变量是连续的,幅值也是连续的。
离散时间信号指的是信号的时间变量是离散的,幅值并没有量化。
数字信号是指离散时间信号的幅值是量化的。
离散时间信号的定义
离散时间信号在数学上被表示为序列。一个序列\(x[n]\),通常用以下形式书写:
\(\displaystyle x[n], \quad -\infty < n < \infty\)
其中\(n\)是一个整数。在实际情况下,这种序列通常是通过对模拟信号(即连续时间信号)\(x_a(t)\)进行周期性抽样而产生的。在这种情况下,序列中的第\(n\)个数的数值等于模拟信号\(x_a(t)\)在时间\(nT\)时的值,即:
\(\displaystyle x[n] = x_a(nT), \quad -\infty < n < \infty\)
其中\(T\)是抽样周期,其倒数是抽样频率。尽管序列不总是来自对模拟信号的抽样,但习惯上将\(x[k]\)称为序列的”第\(k\)个样本”。我们以下图的方式图形化地表示离散时间信号(即序列)。尽管横坐标绘制成连续线,但重要的是要认识到\(x[n]\)仅在整数值的n上有定义。不能认为当n不是整数时\(x[n]\)等于零;对于非整数值的\(n\),\(x[n]\)是未定义的。

在这里,离散时间信号与序列的概念是等价的。
几种常见的序列
单位抽样序列
\(\displaystyle \delta[n]=\left\{\begin{array}{ll}1, & n=0 \\ 0, & n \neq 0\end{array}\right.\)
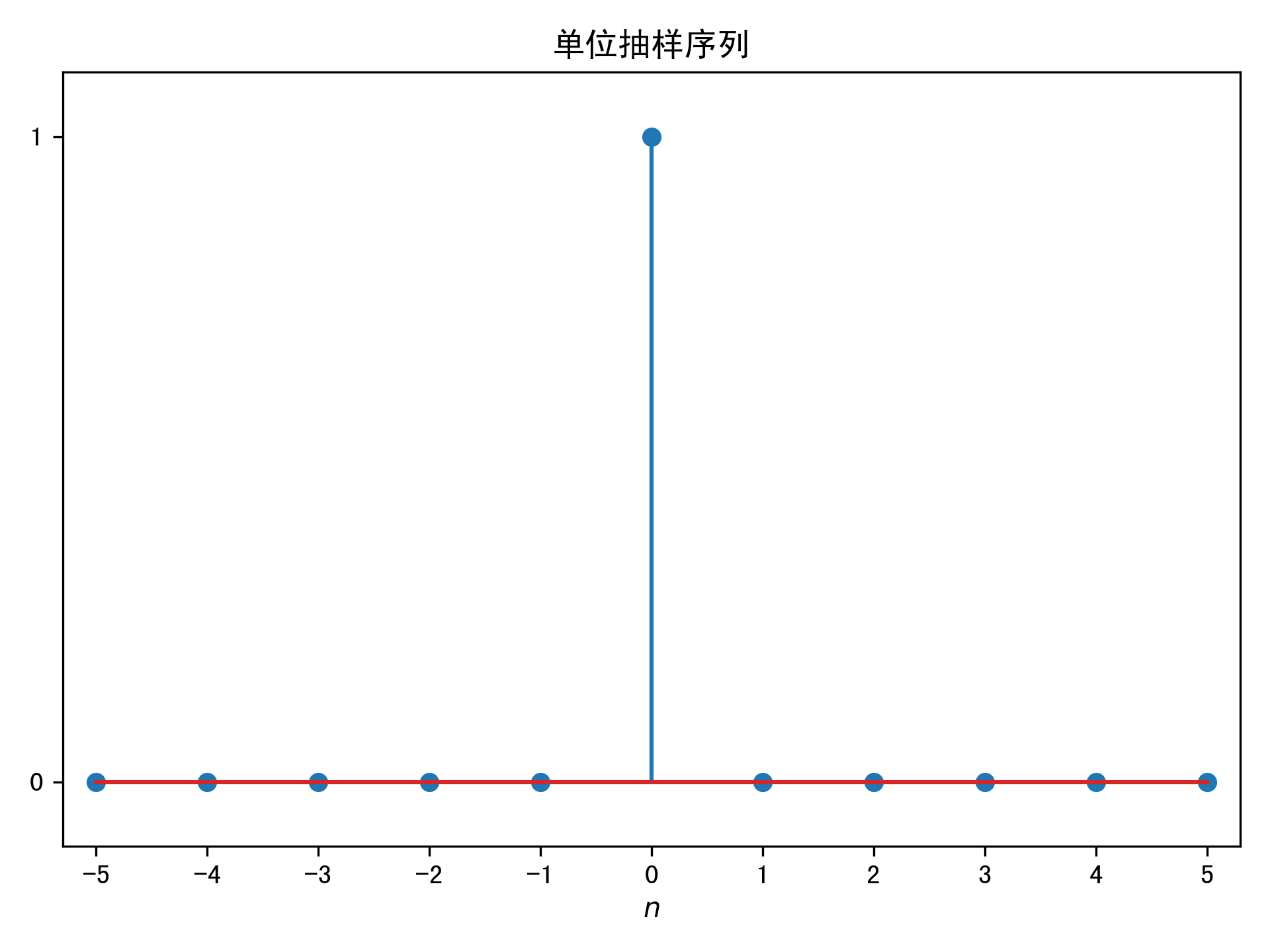
单位阶跃序列
\(\displaystyle u[n]=\left\{\begin{array}{ll}1, & n \geq 0 \\ 0, & n<0\end{array}\right.\)

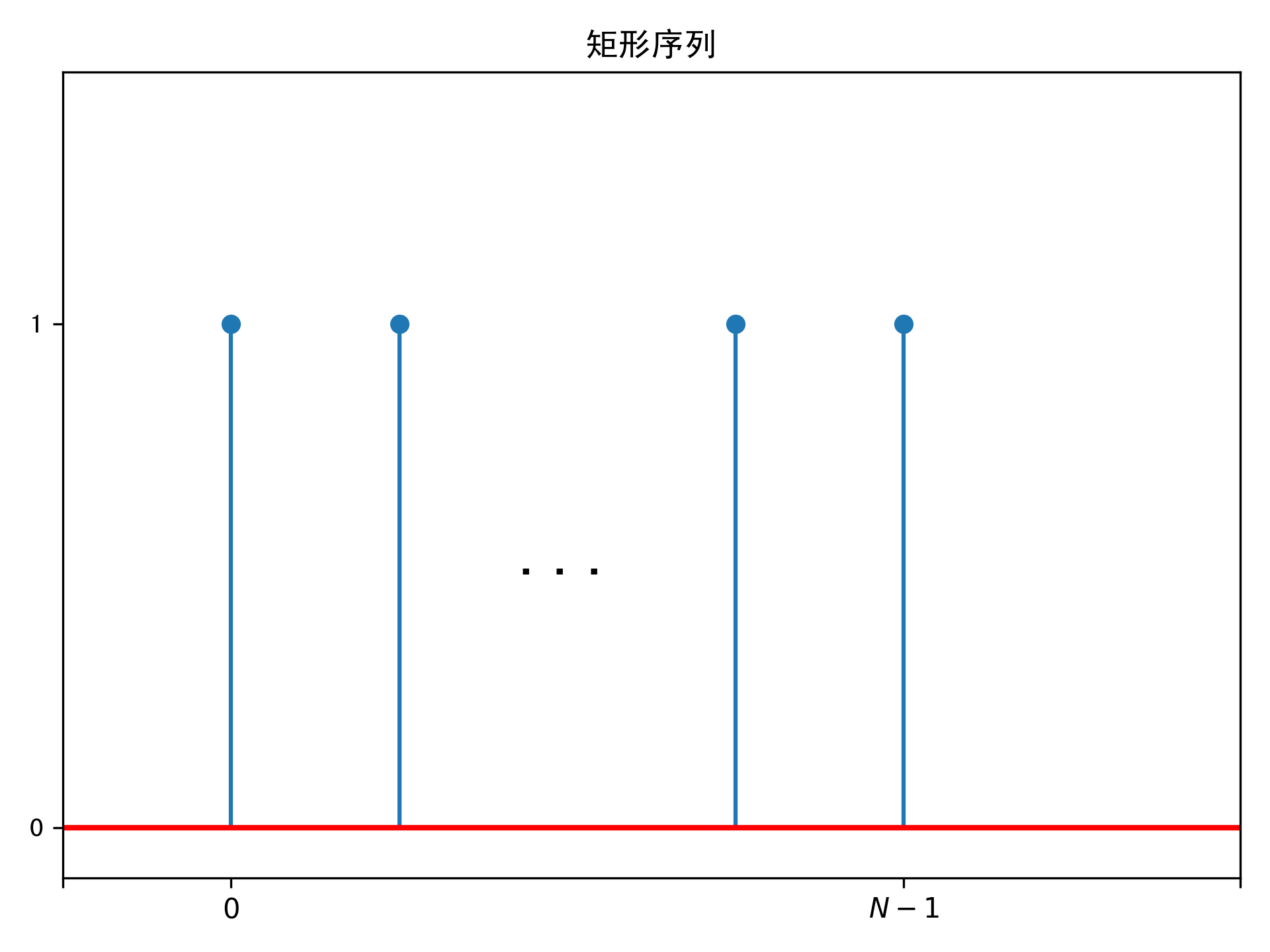
矩形序列
\(\displaystyle \operatorname{rect}[n]=\left\{\begin{array}{ll}1, & 0 \leq n \leq N-1 \\ 0, & \text { 其他 }\end{array}\right.\)
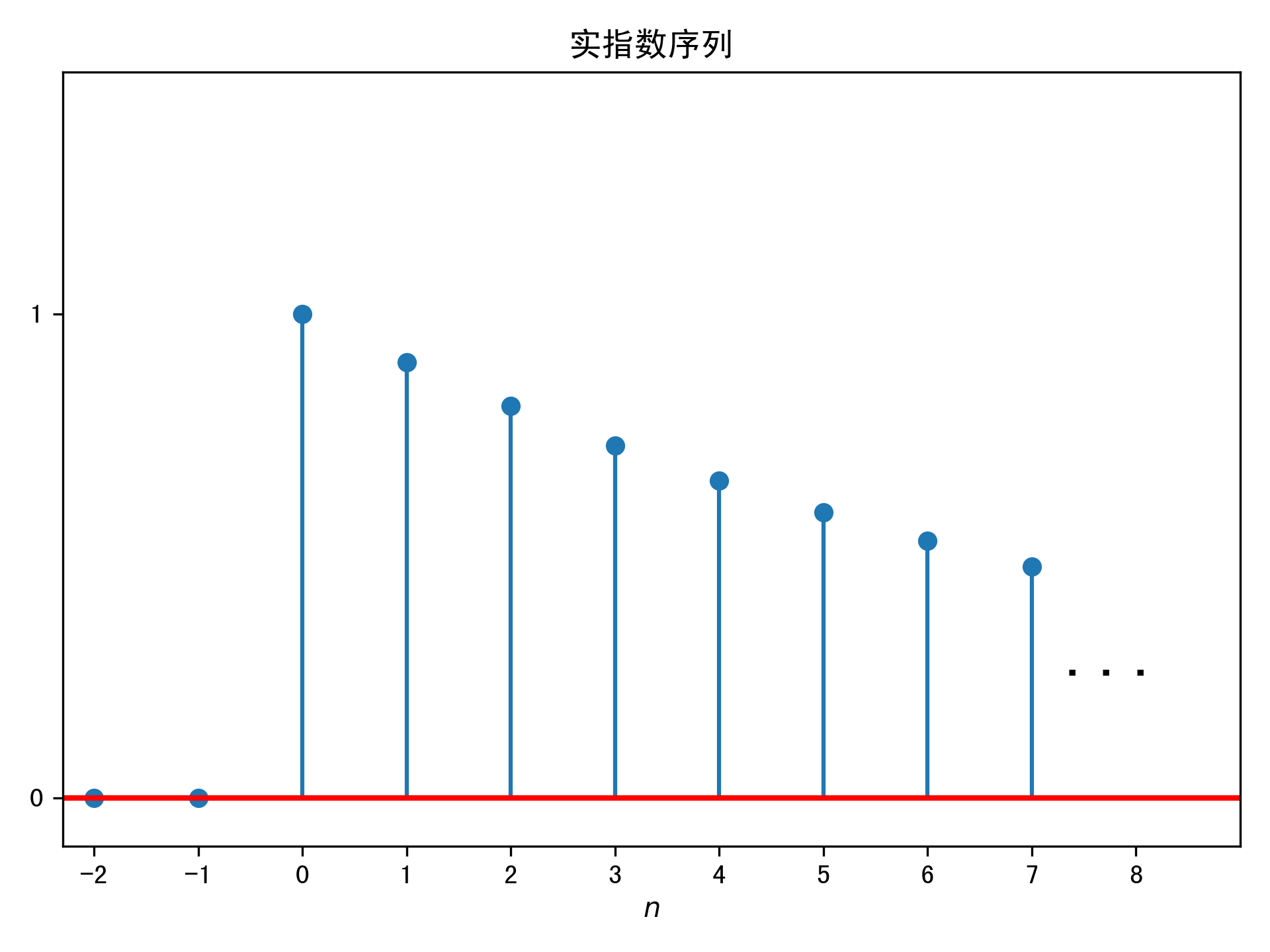
实指数序列
\(\displaystyle x[n]=\alpha^{n} u[n]\)
其中,\(\alpha\)是常数,\(u[n]\)是单位阶跃序列。当\(|\alpha|>1\)时,序列发散;当\(|\alpha|<1\)时,序列是收敛的。
复指数序列
\(\displaystyle x[n]= e^{j(\omega n +\theta)}\)
它可以分解成实部和虚部:
\(\displaystyle x[n]=\cos (\omega n+\theta)+j \sin (\omega n+\theta)\)
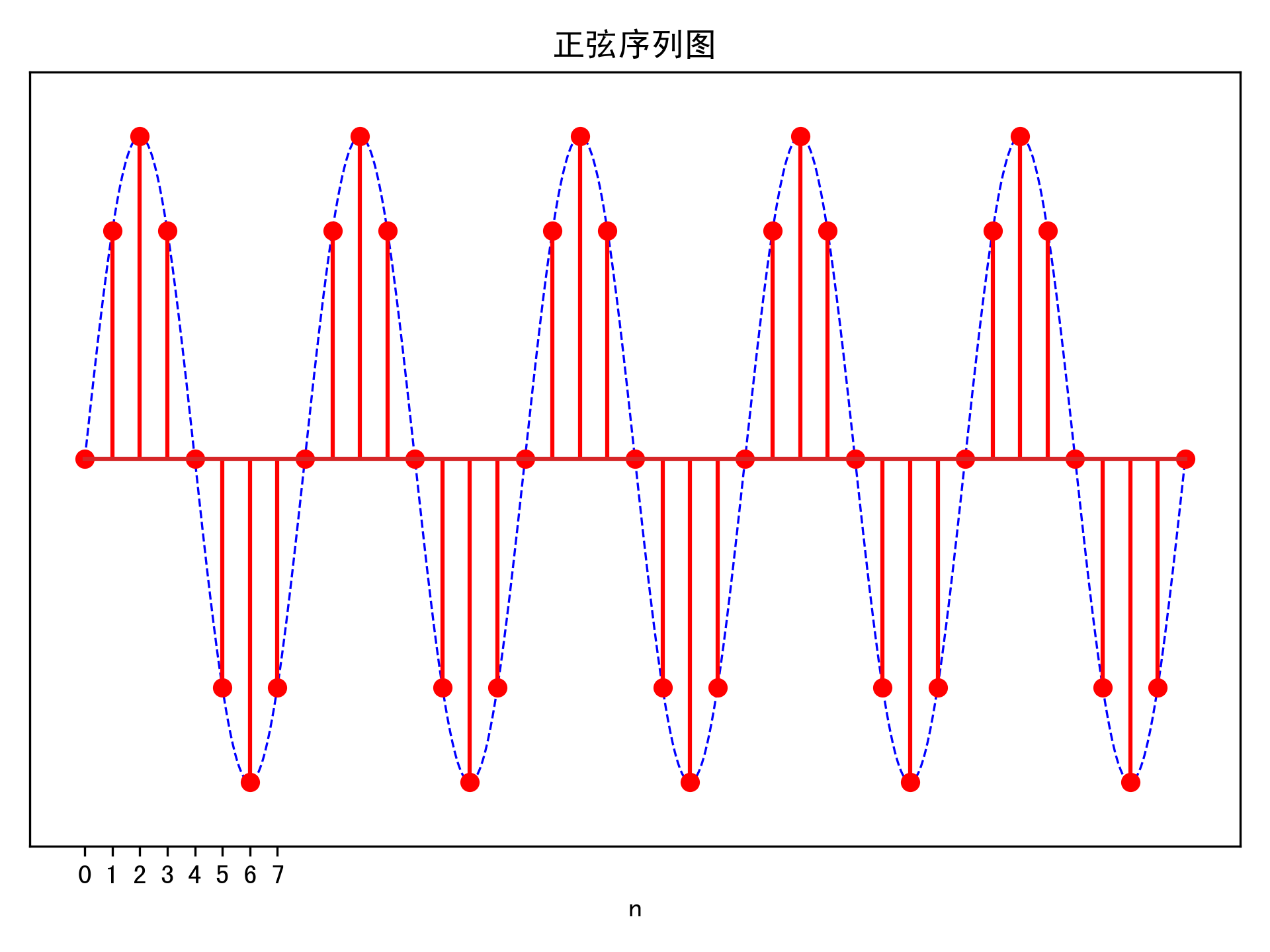
正弦序列
\(\displaystyle x[n]=A \sin (\omega n+\theta)\)
其中,\(A\)和\(\theta\)是常数,\(\omega\)是角频率。
周期序列的定义:当存在一个正整数\(N\),使得\(x[n]=x[n+N]\)对所有的\(n\)成立时,序列\(x[n]\)是周期序列,\(N\)是序列的周期。
不是所有的正弦序列都是周期的,只有当满足下列条件时,正弦序列才是周期的:
\(\displaystyle \omega =\frac{2\pi k}{N}\)
其中,\(k\)是一个整数,\(N\)是正弦序列的周期。
注意:正弦信号一定是周期的,但正弦序列不一定是周期的。
序列的运算
序列的移位
序列的移位是指将序列中的每个数向左或向右移动\(m\)个位置。我们用下面的式子来表示:
\(\displaystyle y[n]=x[n-m]\)
如果\(m\)是一个正整数,表示向右移动\(m\)位,如果\(m\)是一个负整数,表示向左移动\(m\)位。
序列的翻褶
序列的翻褶是指将序列中的每个数按照相反的顺序排列。我们用下面的式子来表示:
\(\displaystyle y[n]=x[-n]\)
序列的累加
序列的累加表达式如下:
\(\displaystyle y[n]=\sum_{k=-\infty}^{n} x[k]\)
它表示序列\(x[n]\)中从\(-\infty\)到\(n\)的所有数的和。
序列的卷积和
给定两个离散时间信号\(x[n]\)和\(h[n]\),它们的卷积和定义为:
\(\displaystyle y[n]=x[n]*h[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]\)
其中,\(*\)表示卷积运算,\(y[n]\)称为\(x[n]\)和\(h[n]\)的卷积和。
给定\(x[n]\)的信号长度为\(L_1\), \(h[n]\)的信号长度为\(L_2\),则卷积和\(y[n]\)的信号长度为\(L_1+L_2-1\)。
例:给定\(x[n]=\{1,3,5\}\),\(h[n]=\{1,2\}\),求\(x[n]\)和\(h[n]\)的卷积和\(y[n]\)。
方法一:我们用矩阵的形式来计算卷积和\(y[n]\),由于\(x[n]\)和\(h[n]\)的信号长度分别为3和2,所以\(y[n]\)的信号长度为\(L_1+L_2-1=4\),我们让\(y=[y[0],y[1],y[2],y[3]]^T\)是一个\(4\times1\)的列向量,则有:
其中,\(H\)是一个\(4\times3\)的变换矩阵。
如果单从矩阵计算来看,可以将\(h[n]\)通过补零扩展成一个\(4\times1\)的列向量,就是\(H\)的第一列,第二列是\(h[n]\)右移一位,第三列是\(h[n]\)右移两位,这样就可以很简便地把这个变换矩阵写出来。
方法二:我们也可以将\(h[n]\)等效成两个单位抽样序列的相加,即\(h[n]=\delta[n]+2\delta[n-1]\),于是\(y[n]=x[n]*h[n]=x[n]+2x[n-1]\),我们可以用图形的方式来表示卷积和的计算过程,如下图所示:
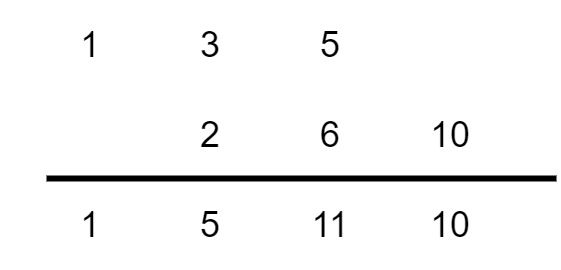
方法三:从以上推导可以看出如果我们设置\(x[n]\)和\(h[n]\)为多项式系数的向量,卷积和的运算也等于这两个多项式相乘的运算,即:
\(\displaystyle (x^2+3x+5)(x+2)=x^3+5x^2+11x+10\)
因此,多项式相乘后的结果的系数向量就是卷积和的结果。
任一序列跟单位抽样序列的卷积和等于序列本身。
\(\displaystyle x[n]=x[n]*\delta [n]\)
任一序列跟单位抽样序列的移位序列的卷积和等于该序列做相同移位的移位序列。
\(\displaystyle x[n-m]=x[n]*\delta [n-m]\)
序列的相关
序列的相关是指两个序列之间的相互关系。假定两个序列\(x[n]\)和\(h[n]\),则这两个序列的相关定义如下:
\(\displaystyle r_{x h}[m]=\sum_{n=-\infty}^{\infty} x[n] h[n-m]\)
上面的定义是基于两个信号是确定性信号且为能量信号的情况。如果两个信号是随机信号,则需要使用基于期望值的与之不同的定义(读者可以参考随机过程的书籍)。
当\(h[n]=x[n]\)时,相关就是自相关。自相关的定义如下:
\(\displaystyle r_{x x}[m]=\sum_{n=-\infty}^{\infty} x[n] x[n-m]\)
\(r_{x x}[m]\)是实偶序列,即\(r_{x x}[m]=r_{x x}[-m]\);
\(r_{x x}[0]\)是\(x[n]\)的能量,且\(r_{x x}[0] > |r_{x x}[m]|\)
自相关可以用卷积来表示:
\(\displaystyle r_{x x}[m]=x[m]*x[-m]\)
相关用来衡量两个信号之间的相似性,卷积则表示信号通过系统的一种运算。
思考题
判断下列序列是否是周期序列,如果是,求出它的周期:
\(\displaystyle x[n]= A \cos (\frac{3\pi}{10} n+\frac{\pi}{4})\)
\(\displaystyle x[n]= e^{j\pi n/\sqrt{5}}\)
\(\displaystyle x[n]= e^{j(\frac{\pi}{6}-\frac{\pi}{2})}\)
已知\(x[n]=\{1,2,3,4\}\),\(h[n]=\{1,2\}\),
(1)求\(x[n]\)和\(h[n]\)的卷积和\(y[n]\);
(2)求\(x[n]\)的自相关函数\(r_{x x}[n]\)。