#! https://zhuanlan.zhihu.com/p/658011619
抽样定理
奈奎斯特抽样定理:要从抽样信号中无失真地恢复原信号,抽样频率应大于或等于信号最高频率的两倍。
证明:假设带限的原信号为\(x_a(t)\),抽样信号为\(\hat x_a(t)\),抽样间隔为\(T\),抽样角频率为\(\Omega_s=2\pi/T\)。连续时间信号理想抽样的过程在数学上可以表示为原信号乘以一个冲激脉冲序列\(\sum_{n=-\infty}^{\infty}\delta(t-nT)\),即
\(\displaystyle \hat x_a(t)=x_a(t)\sum_{n=-\infty}^{\infty}\delta(t-nT)\)
下面研究理想抽样信号的频谱特性。根据傅里叶变换的性质,时域相乘对应频域卷积,即
\(\displaystyle \hat X_a(j\Omega) = \frac{1}{2\pi}X_a(j\Omega)* \mathcal{FT}\{\sum_{n=-\infty}^{\infty}\delta(t-nT)\}\)
冲激脉冲序列\(\displaystyle \sum_{n=-\infty}^{\infty}\delta(t-nT)\)的傅里叶变换为\(\displaystyle \sum_{n=-\infty}^{\infty}\Omega_s \delta(\Omega-jn\Omega_s)\),因此
\(\displaystyle \hat X_a(j\Omega) = \frac{1}{T}\sum_{n=-\infty}^{\infty}X_a(j\Omega-jn\Omega_s)\)
上式表明了理想抽样信号的频谱是原信号频谱的周期延拓,且周期延拓的周期为\(\Omega_s\)。由于原信号\(x_a(t)\)的频谱\(X_a(j\Omega)\)是带限信号,即\(X_a(j\Omega)=0\),当\(|\Omega|>\Omega_h\),其中\(\Omega_h\)为原信号的最高频率。因此,只要满足\(\Omega_s \geq 2\Omega_h\),则理想抽样信号的频谱不会发生混叠,原信号可以从理想抽样信号中恢复。
接下来用图形的方法来说明抽样定理。假设原信号\(x_a(t)\)时域和频谱如下图所示,频谱的最高频率为\(\Omega_h\)。
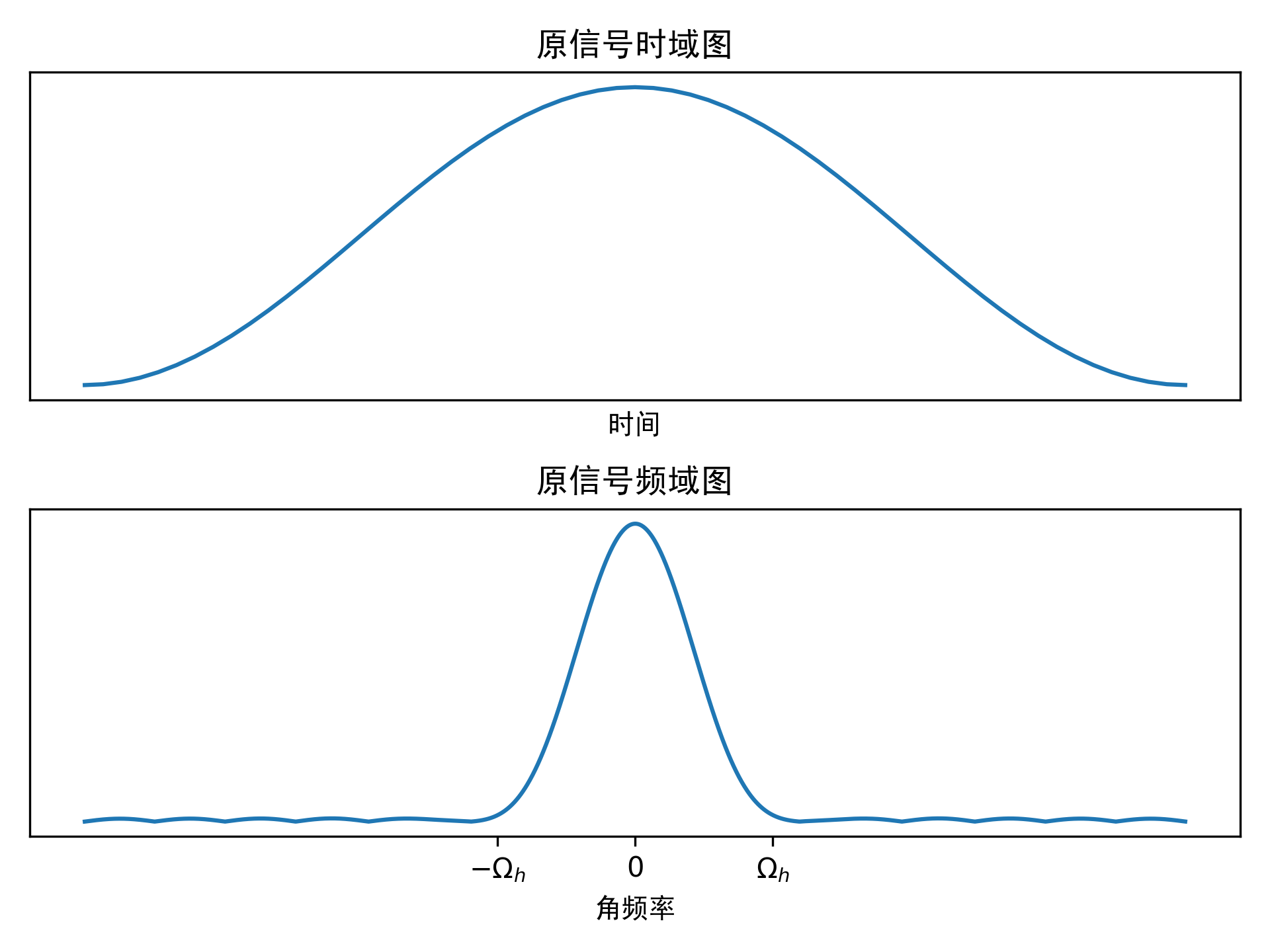
我们在实际中定义信号的最高频率,通常是指信号绝大部分能量集中在这个频率以内,并不需要这个频率点等于0。
根据抽样定理,抽样频率\(\Omega_s\)应满足\(\Omega_s \geq 2\Omega_h\),也可以说是信号的最高频率小于或等于折叠频率,即\(\Omega_h \leq \Omega_s/2\),这里定义了折叠频率为抽样频率的一半,原信号才可以从抽样信号中无失真的恢复,也就是说此时的离散时间信号可以完整地表示连续时间信号。我们用图形表示如下:
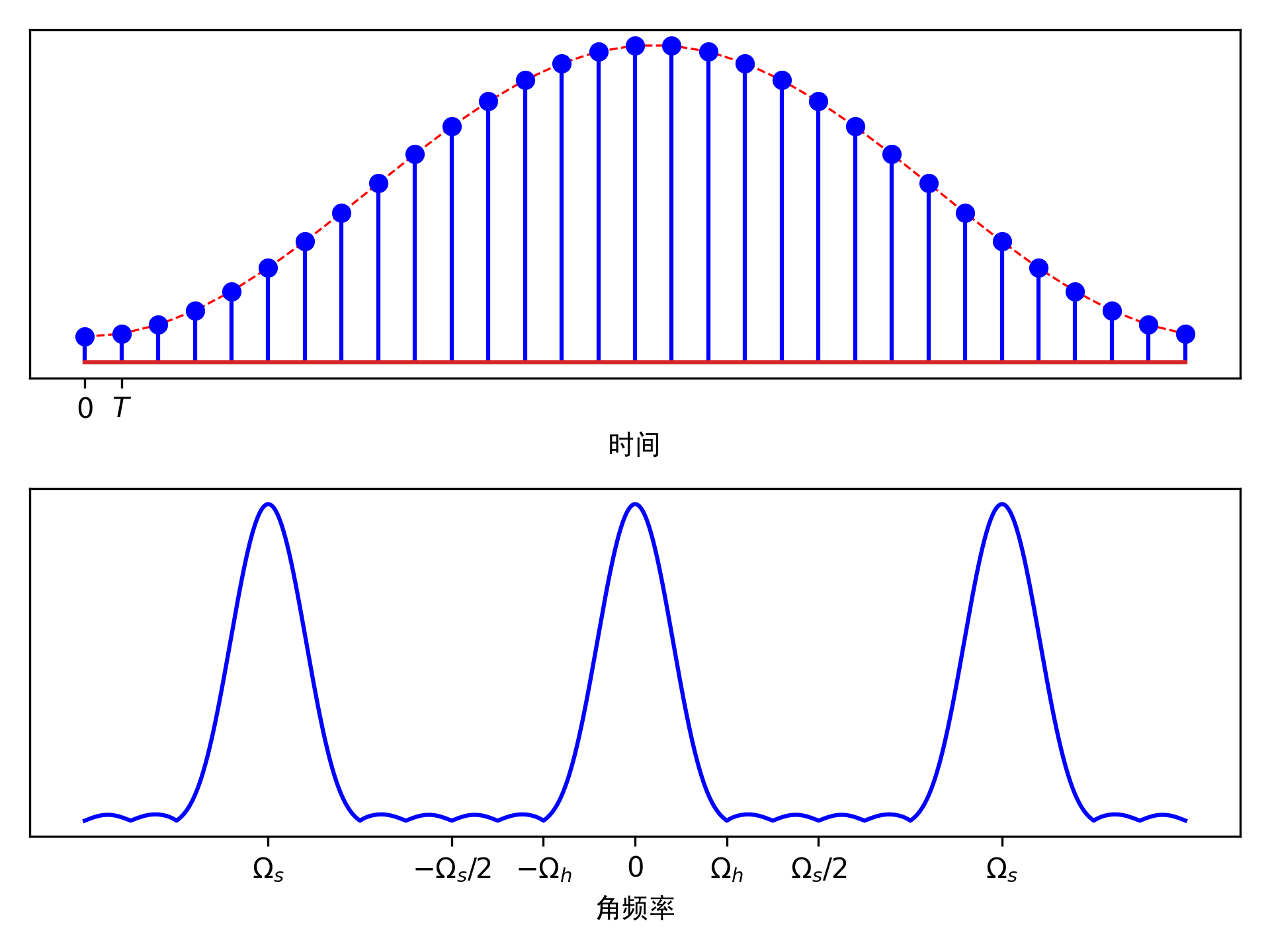
当抽样频率\(\Omega_s < 2\Omega_h\)时,理想抽样信号的频谱如下图所示,信号频率在\((\Omega_s-\Omega_h, \Omega_h)\)之间产生了混叠,混叠后的波形如蓝色曲线所示,这样我们无法从抽样信号的频率中恢复出原信号。
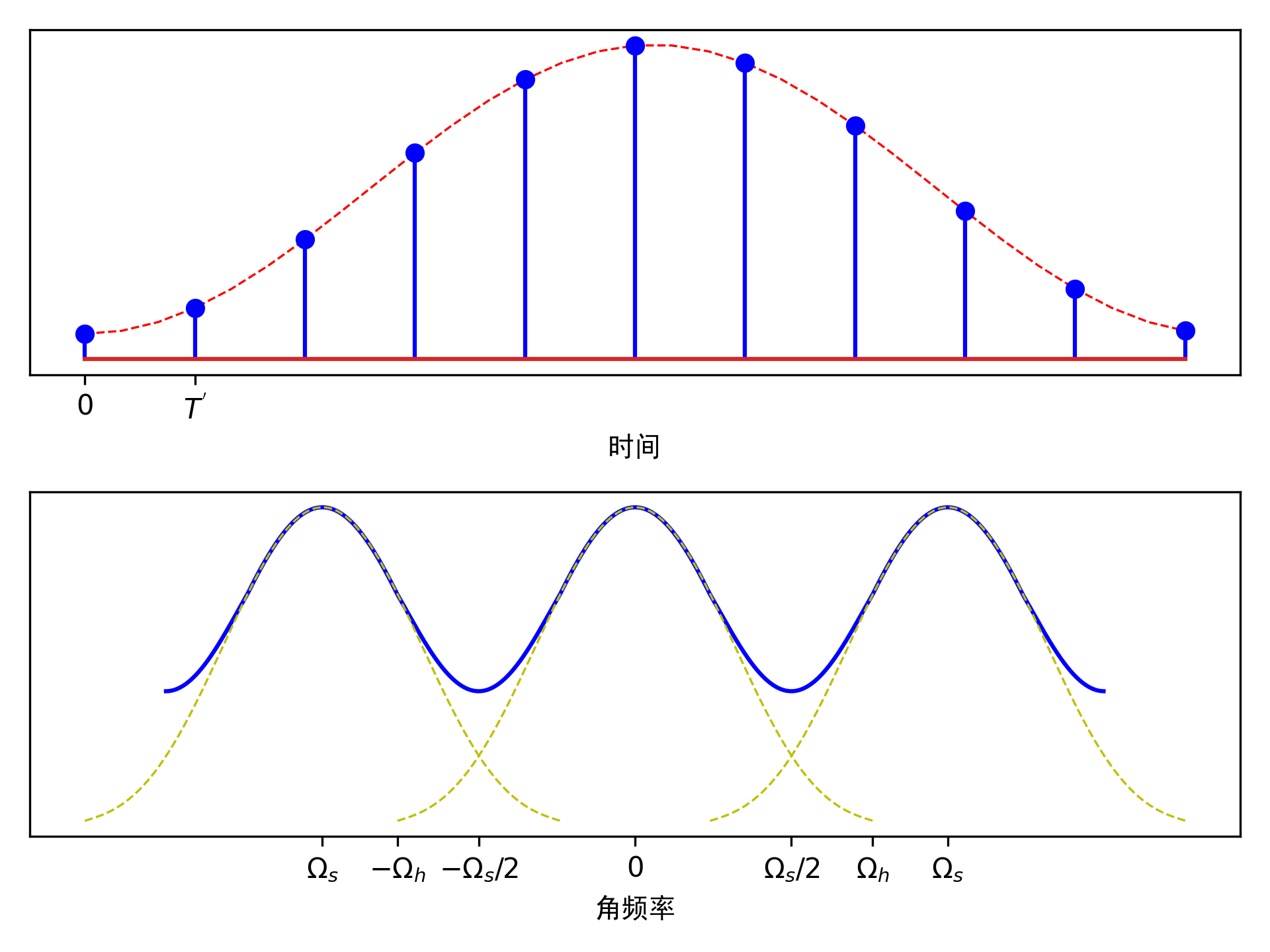
理想抽样信号的重构
理想抽样信号的频谱是原信号频谱的周期延拓,因此可以通过低通滤波器来恢复原信号。如下图所示,可以在折叠频率\(\Omega_s/2\)处设置一个理想低通滤波器,滤除掉其他的周期频率分量,从而恢复原信号。这个地方理想低通滤波器的幅值是\(T\),是因为理想抽样信号的频谱是原信号频谱的\(\frac{1}{T}\)倍,因此需要乘以\(T\)倍才能恢复原信号的幅值。
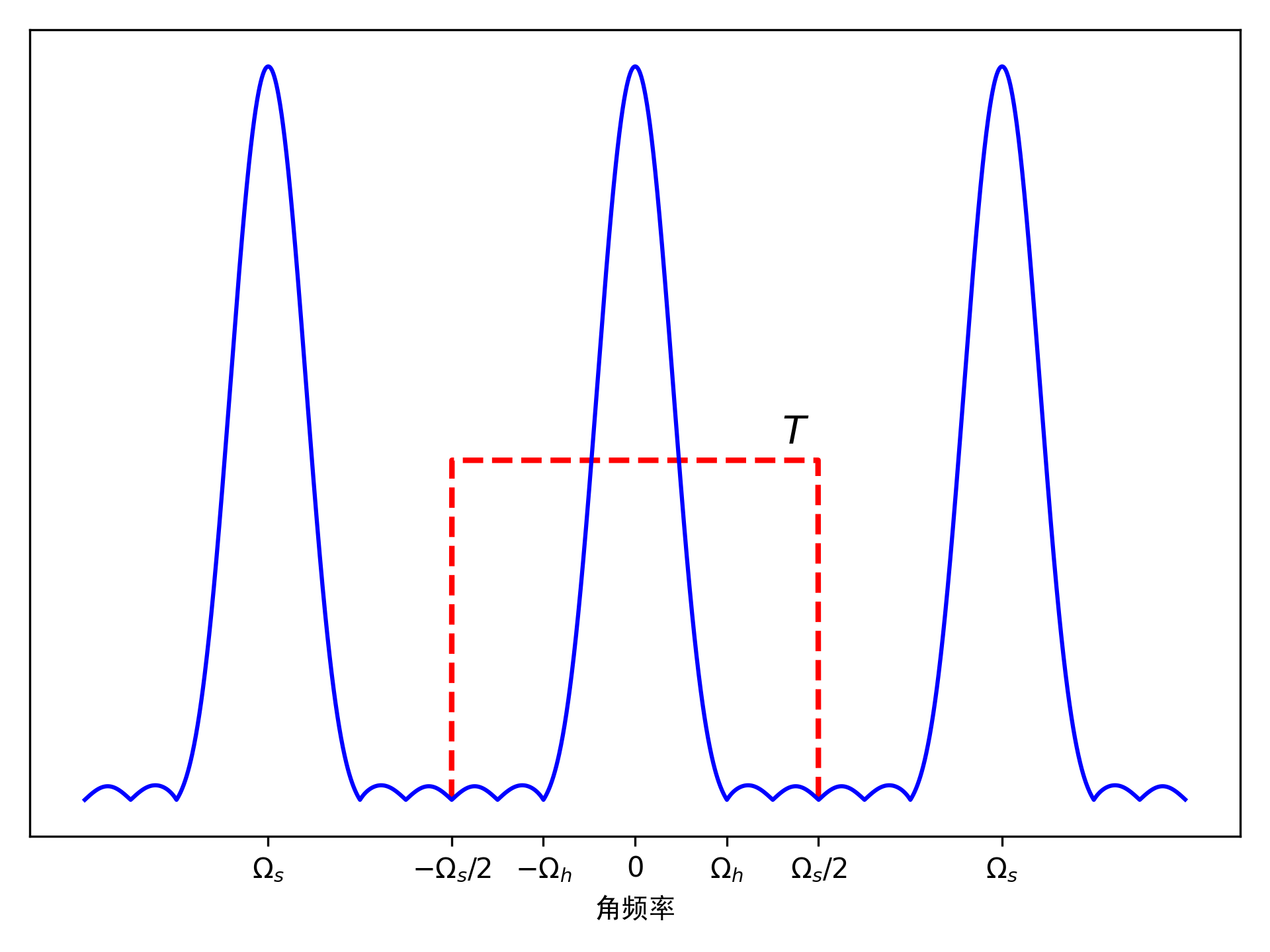
根据傅里叶变换性质,频域乘积导致时域卷积,因此重构信号在时域 表达式为:
其中\(h(t)\)为理想低通滤波器的冲激响应,即\(h(t)=\frac{\sin(\pi t/T)}{\pi t/T}\)。于是可以得到
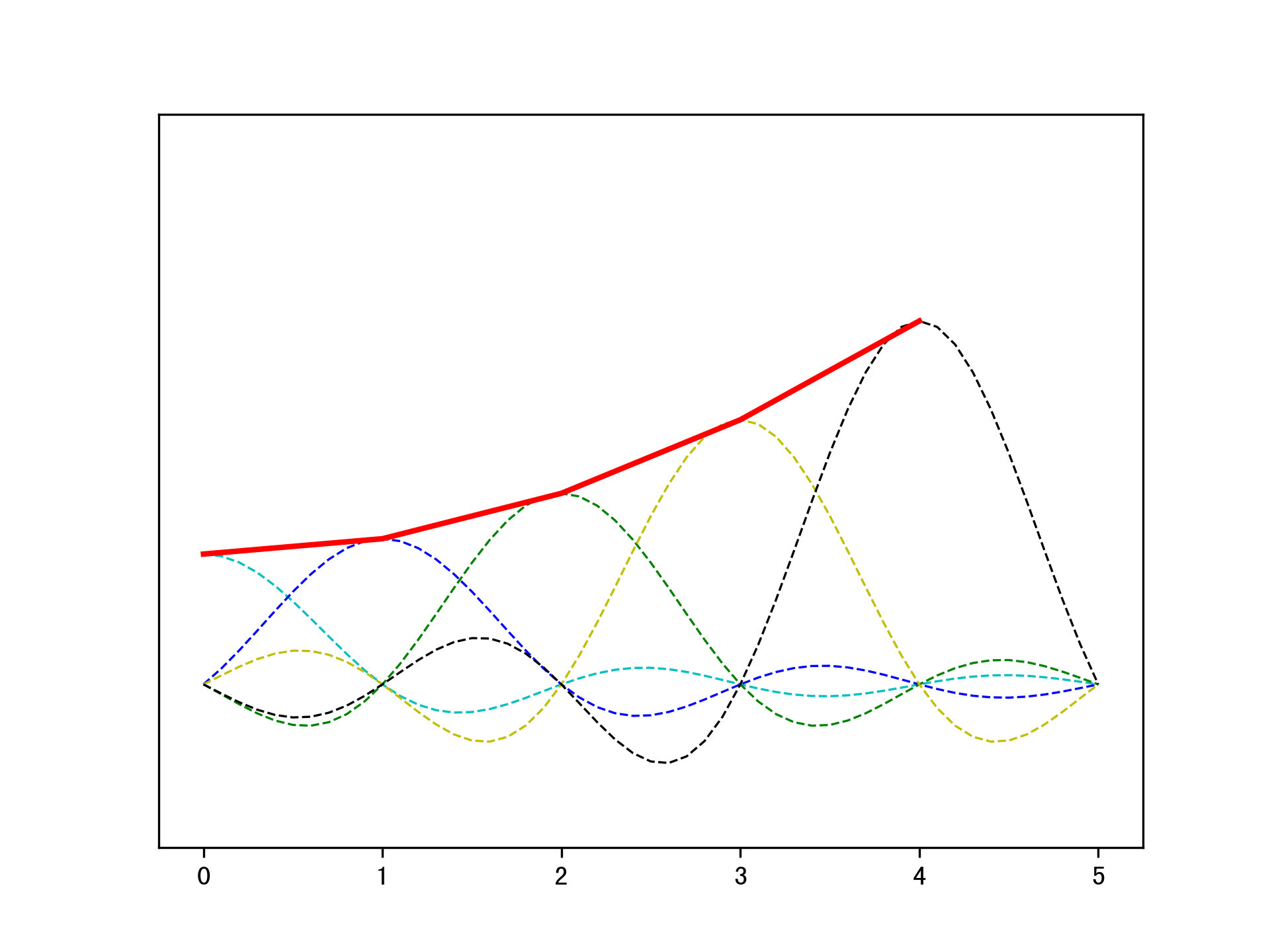
\(\displaystyle x_r(t) = \sum_{n=-\infty}^{\infty}x(n)\frac{\sin(\pi (t-nT)/T)}{\pi (t-nT)/T}\)
这里\(\frac{\sin(\pi (t-nT)/T)}{\pi (t-nT)/T}\)是一个sinc函数,称之为内插函数,当\(t=nT\)时,它为1,在其他的抽样点上,它的值为0。
下图是从理想抽样信号重构原信号的过程。我们是用上面的公式重构了前5个抽样点时信号的时域波形,随着更多的\(sinc(t)\)函数的叠加,重构信号将会越来越平滑且接近原信号。