#! https://zhuanlan.zhihu.com/p/663306670

快速傅里叶变换（FFT）之一：Radix-2 DIT FFT

引言

快速傅里叶变换（FFT）是一种高效的计算DFT的算法，它的计算复杂度为\(O(N\log N)\)，而直接计算DFT的计算复杂度为\(O(N^2)\)。本文将介绍Radix-2 DIT FFT算法的基本原理。

预备数学等式

\(\displaystyle W_{Nm}^{nkm} = W_{N/m}^{nk/m}=W_N^{nk} = e^{-j\frac{2\pi n k}{N}}\)

\(\displaystyle W_N^{N/2} = -1\)

基本原理

设序列\(x[n]\)的长度为\(N=2^M\)，\(M\)为整数。如果不满足这个条件，可以通过补零，使之达到这个要求。我们通过在时域上的抽取将\(x[n]\)分为两个长度为\(N/2\)的子序列如下：

\(\displaystyle x_1[n] = x[2n]\)

\(\displaystyle x_2[n] = x[2n+1]\)

则\(x[n]\)的DFT可以表示为：

\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k)& =\sum_{n=0}^{N-1}x[n]W_N^{nk} \\ & = \sum_{n=0}^{N/2-1}x[2n]W_N^{2nk} + \sum_{n=0}^{N/2-1}x[2n+1]W_N^{(2n+1)k} \\ & = \sum_{n=0}^{N/2-1}x_1[n]W_{N/2}^{nk} + W_N^{k}\sum_{n=0}^{N/2-1}x_2[n]W_{N/2}^{nk} \\ & = X_1(k) + W_N^kX_2(k) \end{split}\end{equation*}\end{split}\]

其中，\(X_1(k)\)和\(X_2(k)\)分别为\(x_1[n]\)和\(x_2[n]\)的\(N/2\)点的DFT，\(k=0,1,\cdots,N/2-1\)，\(W_N^k\)为旋转因子。通过上面的公式，我们只计算出来了\(k=0,1,\cdots, N/2-1\)的\(X[k]\)。对于\(k=N/2,N/2+1,\cdots,N-1\)，我们可以通过下面的公式计算：

\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k+N/2)& = X_1(k+N/2) + W_N^{k+N/2}X_2(k+N/2) \\ & = X_1(k) - W_N^kX_2(k) \end{split}\end{equation*}\end{split}\]

我们可以用下面的示意图表示上述的过程：

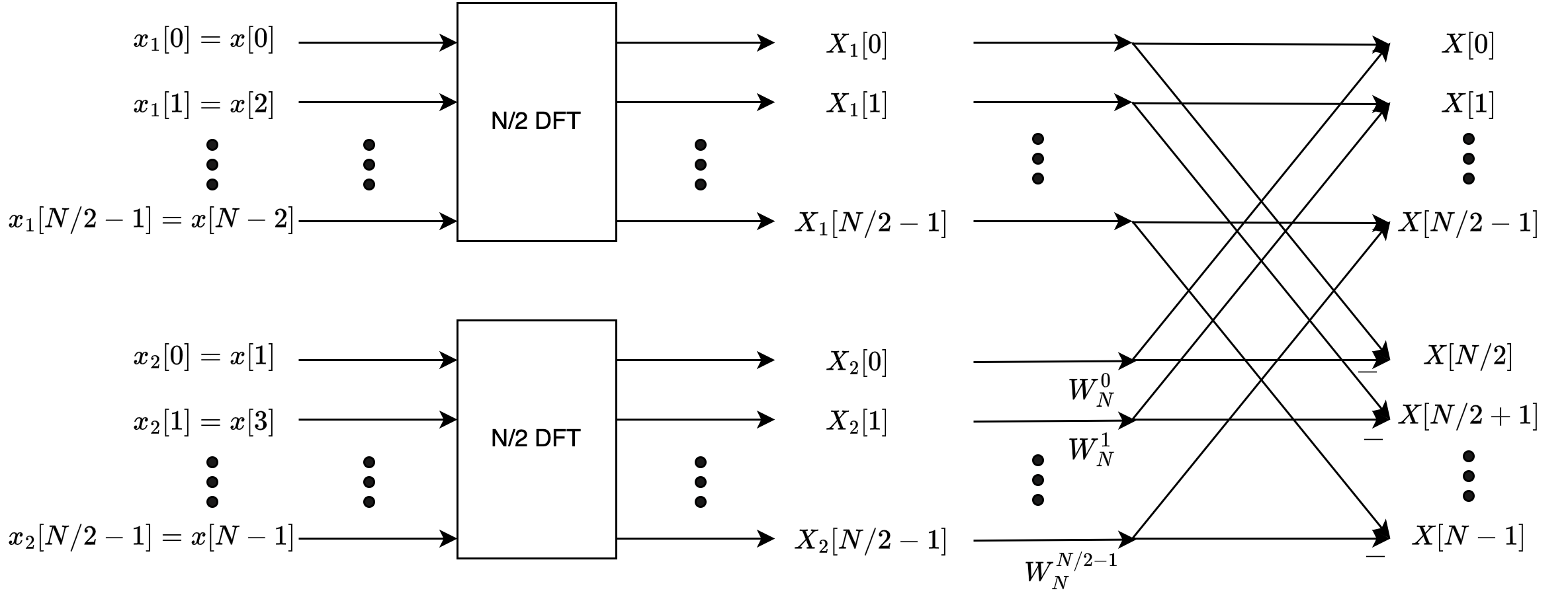
图中的蝶形结构称为Radix-2 DIT蝶形结构。可以用下图来表示：

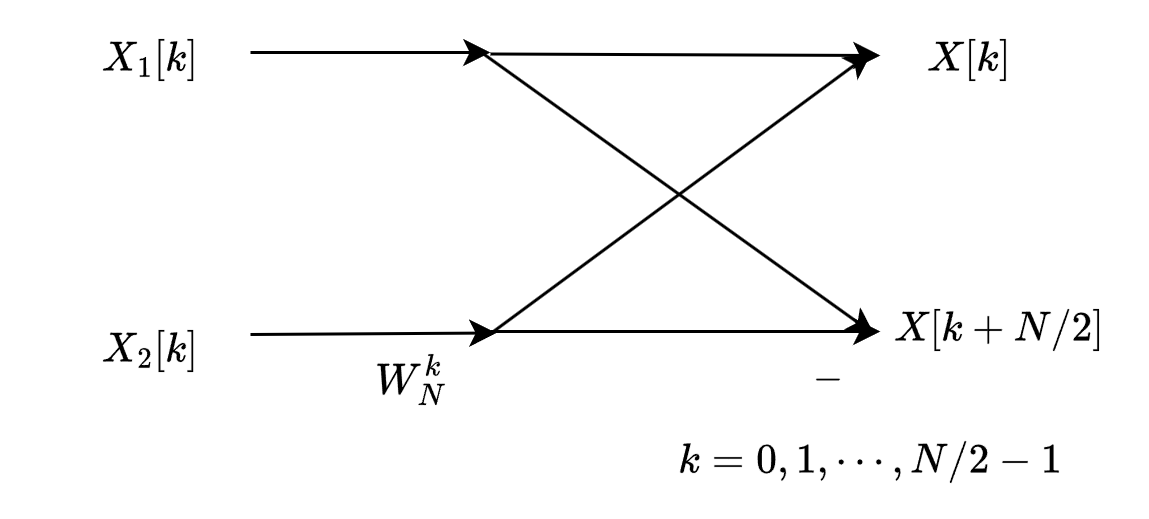
Radix-2 DIT蝶形运算

从上图可以看出每一次蝶形运算需要1次复数乘法，两次复数加法。通过将\(x[n]\)在时间上抽取后，N点的DFT变换，现在变成了两个N/2点的DFT，再加上右边的N/2个蝶形运算，因此计算的复杂度为：\(O(N^2/4+N^2/4+N/2)\)，即约为\(O(N^2/2)\)。计算量相比之前已经减半了。我们可以按照这种分而治之(divide and conquer)的思路继续将\(x_1[n]\)和\(x_2[n]\)分别抽取为两个长度为\(N/4\)的子序列，然后再进行蝶形运算。我们将\(x_1[n]\)的抽取过程画出来：

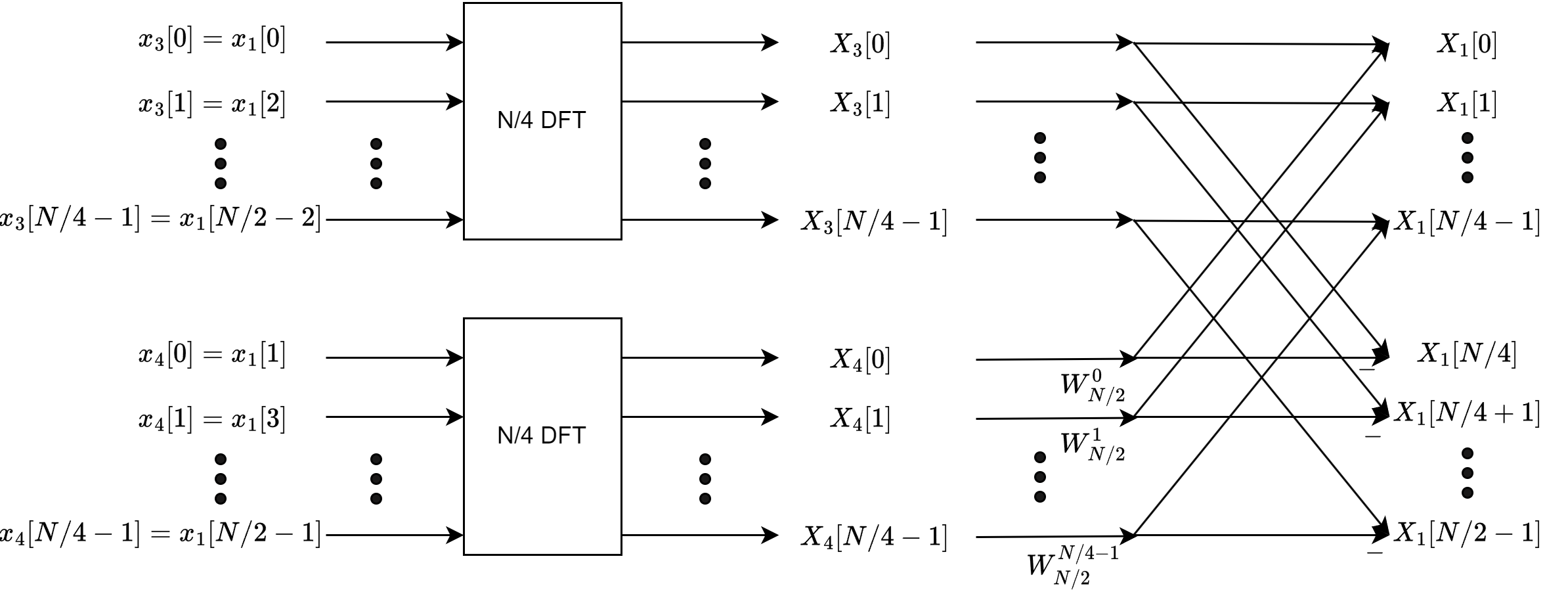
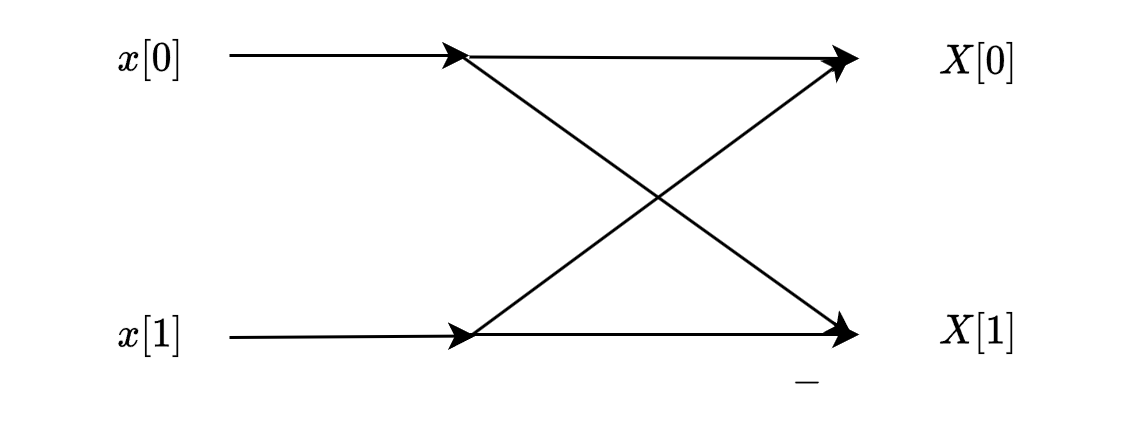
我们可以继续用上述的方法将每个子序列继续划分，直到最后序列长度为2。2点的DFT计算如下：

\[\begin{split}\displaystyle \begin{bmatrix} X[0] \\ X[1] \end{bmatrix} =\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix}\cdot \begin{bmatrix} x[0] \\ x[1] \end{bmatrix} \end{split}\]

我们也可以用蝶形运算来表示：

通过这种思想，以8点的DFT计算为例，我们画出了Radix-2 DIT FFT的计算流程图如下：

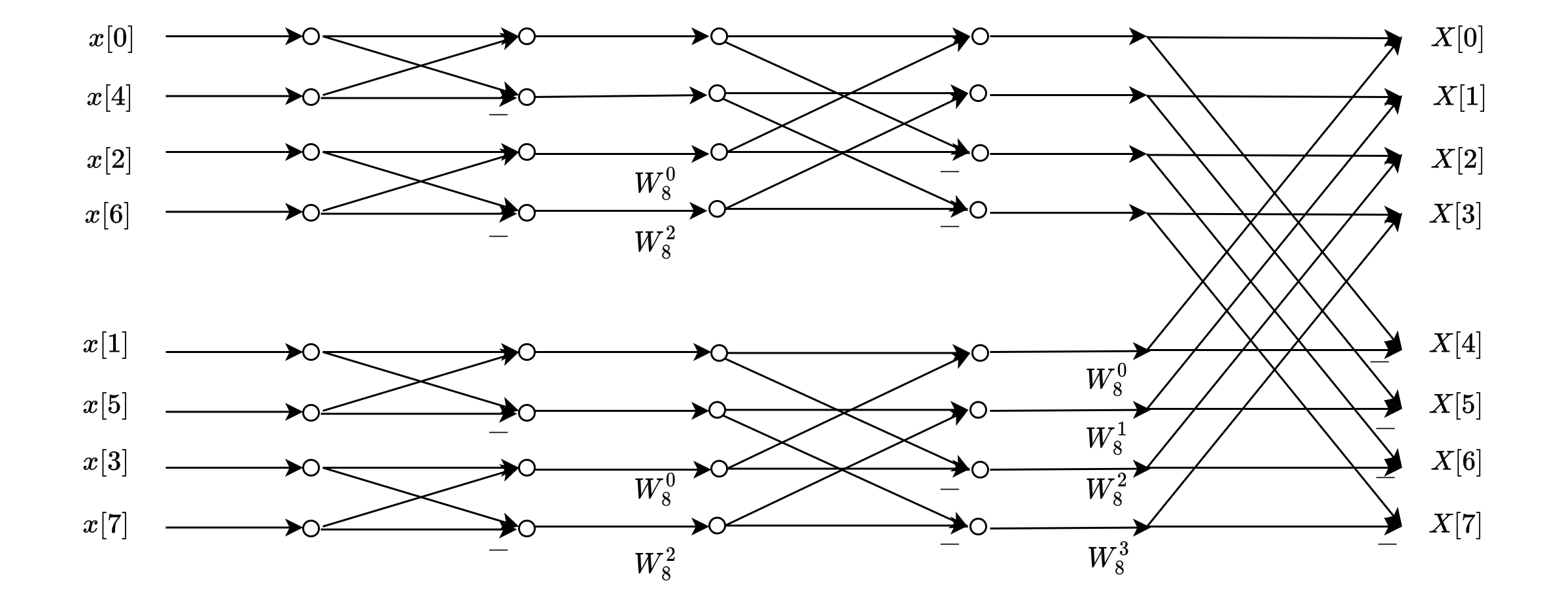
计算复杂度

在Radix-2 DIT FFT算法中，\(N\)点FFT由\(\log_2 N\)个阶段组成，每个阶段由\(N/2\)点的Radix-2 DIT蝶形结构组成。每个蝶形结构运算需要1次复数乘法和2次复数加法。因此，Radix-2 DIT FFT计算总共需要的复数乘法数量为\(N/2\log_2N\)，复数加法的数量为\(N\log_2 N\)。如果剔除掉旋转因子\(W_N^0\)这种乘法，那所需的乘法次数会更少。

实现分析

输入为倒位序，输出为自然顺序

Radix-2 DIT FFT算法，信号时域的输入为倒位序，频域的输出为自然顺序。倒位序指的是将输入序列的二进制位反转。我们用下面的表格表示8点的倒位序和自然顺序关系：

自然顺序	自然顺序二进制	倒位序二进制	倒位序
0	000	000	0
1	001	100	4
2	010	010	2
3	011	110	6
4	100	001	1
5	101	101	5
6	110	011	3
7	111	111	7

倒位序的具体实现可以参考Gold-Rader位反转算法。

蝶形运算与旋转因子

\(N\)点FFT由\(\log_2 N\)个阶段组成，最后一个阶段的旋转因子如下：

\(\displaystyle \{W_N^{0}, W_N^{1},\cdots,W_N^{N/2-1}\}\)

倒数第二阶段的旋转因子如下：

\(\displaystyle \{W_{N/2}^{0}, W_{N/2}^{1},\cdots,W_{N/2}^{N/4-1}\}\)

我们也可以表示成：

\(\displaystyle \{W_{N}^{0}, W_{N}^{2},\cdots,W_{N}^{N/2-2}\}\)

因此在FFT的计算中，我们只需要存储\(N/2\)个旋转因子即可，而且每一阶段的旋转因子的选取都遵循一定的规律，这非常有利于编程实现。具体的规律如下：

每一阶段蝶形运算节点距离为\(2^{m-1}\)，其中\(m=1,2,\cdots,\log_2{N}\)为阶段数。每一阶段的蝶形运算的旋转因子\(W_N^r\)中\(r\)的确定可以用下面的运算实现：

将\(k\)写成\(\log_2{N}\)位二进制的形式，其中\(k=0,1,\cdots,2^{m-1}-1\)；
将此二进制数左移\(\log_2{N}-m\)位，把右边空出的位置补零，结果即为\(r\)。

同址运算

在Radix-2 DIT FFT算法中，我们可以发现，每个阶段的蝶形运算都是在前一阶段的序列上进行的，因此蝶形运算的输出能够被存储在之前用于蝶形运算输入数据的同样的硬件存储器内，不需要中间存储器。这种运算方式称为同址运算(in-place computation)。同址运算可以节省内存空间。