#! https://zhuanlan.zhihu.com/p/656731198

傅里叶级数，傅里叶变换与拉普拉斯变换

傅里叶级数

任何一个周期函数都可以表示成一系列谐波相关的三角函数的和。
— 约瑟夫·傅里叶

假定周期信号$x(t)=x(t+T)$，其中$T$为周期，$x(t)$的傅里叶级数可表示为： $$\displaystyle x(t)=\frac{1}{2}a_0+\sum_{n=1}^{\infty}(a_n\cos n\Omega_0 t+b_n\sin n\Omega_0 t) $$

其中，$\Omega_0=\frac{2\pi}{T}$定义为基波角频率，$a_n=\frac{2}{T}\int_{T}x(t)\cos({n\Omega_0t})dt$和$b_n=\frac{2}{T}\int_{T}x(t)\sin({n\Omega_0t})dt$为系数，$n$为谐波次数。如果用复指数函数来表示，则有：

$\displaystyle x(t)=\sum_{n=-\infty}^{\infty}c_n e^{jn\Omega_0 t}$

复数系数$c_n$与$a_n$和$b_n$关系如下：

\[c_n=\frac{1}{2}(a_n+jb_n)\]

\[c_n=\frac{1}{T}\int_Tx(t)e^{-jn\Omega_0t}dt\]

当初，傅里叶提出用三角函数的级数来表示周期信号的时候，拉格朗日和拉普拉斯是反对的。反对的理由有两个:

傅里叶提交的论文中的证明不严谨；

对于方波这样的不连续的函数用连续的三角函数来表示无法解释。

对于第1个理由，德国数学家P.L.Dirichlet在1829年提出了一种更加严谨的证明方法，即Dirichlet条件。Dirichlet条件是傅里叶级数收敛的充分必要条件，即：

在一周期内，信号是绝对可积的;
在一周期内，极大值或极小值的数目应是有限个的；
在任意有限区间内，x(t)只有有限个第一类间断点。

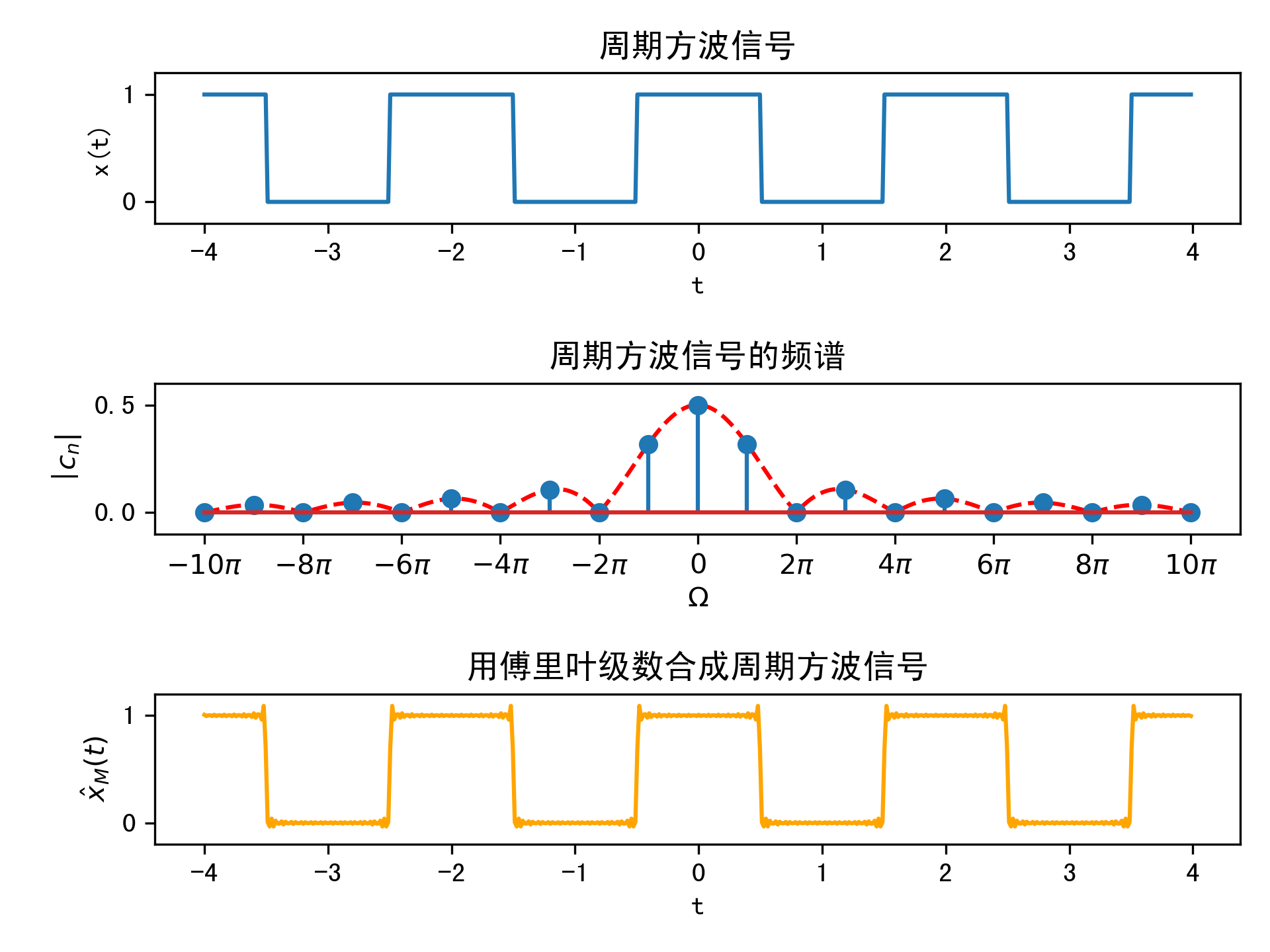
对于第2个理由，数学家们用均方收敛的方法来解释，即对于周期性的方波用连续的三角函数来表示，无法保证合成信号与原信号一致收敛，但是在误差能量趋近于零的均方意义上用傅里叶级数合成的波形跟原方波之间没有区别，均方收敛的数学表达式如下： $$\lim_{M\to\infty}\int_{T}|x(t)-\hat X_M(t)|^2dt=0$$

其中，$\displaystyle \hat X_M(t) = \sum_{n=-M}^{M}c_ne^{jn\Omega_0t}$。周期信号的时域，频域和用傅里叶级数生成的合成信号可以用下图表示：

傅里叶变换

非周期信号可以看成周期为无限长的周期信号。 — 约瑟夫·傅里叶

傅里叶变换是傅里叶级数的推广，随着周期变成无限长，频率分量变成连续的，傅里叶级数的和变成了积分。因此傅里叶变换的正反变换定义为：

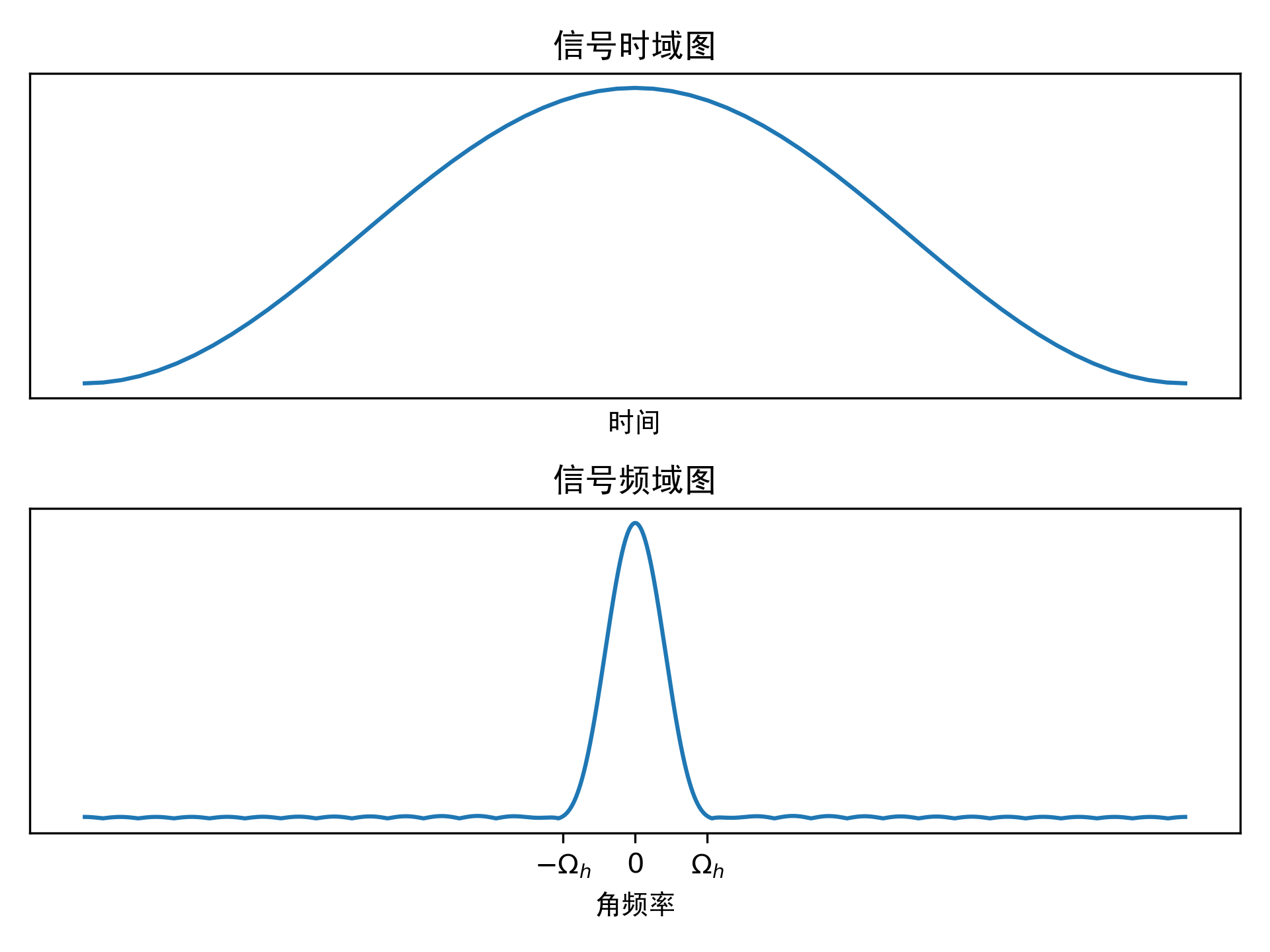
\[X(j\Omega)=\int_{-\infty}^{\infty}x(t)e^{-j\Omega t}dt\]

\[x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(j\Omega)e^{j\Omega t}d\Omega\]

其中$\Omega=2 \pi f$为角频率。下图是脉冲成形信号的时域和频域图。

信号的频率$X(j\Omega)$是一个复函数，它可表示为： $$X(j\Omega)=X_R(j\Omega)+jX_I(j\Omega)=|X(j\Omega)|e^{j\varphi(\Omega)}$$

其中$X_R(j\Omega)$和$X_I(j\Omega)$分别为实部和虚部，$|X(j\Omega)|$为幅度，$\varphi(\Omega)$为相位。如果用频率$f$来表示的话，傅里叶变换正反变换如下:

\[X(f)=\int_{-\infty}^{\infty}x(t)e^{-j2\pi ft}dt\]

\[x(t)=\int_{-\infty}^{\infty}X(f)e^{j2\pi ft}df\]

傅里叶变换架起了信号时域和频域之间的桥梁，可以将信号从时域转换到频域，也可以将信号从频域转换到时域。傅里叶变换存在的充分条件是信号绝对可积，即：

\[\int_{-\infty}^{\infty}|x(t)|dt<\infty\]

通俗来讲，傅里叶变换的作用是将信号分解为不同特征（不同频率）的正弦信号的和，如同化学分析来分析一个化合物的元素成分。对于一个信号，也可对其进行分析，来确定组成它的基本（正弦信号）成分。

拉普拉斯变换

Dirichlet条件要求信号绝对可积，其傅里叶变换才存在，对于一些信号而言无法满足绝对可积的条件，因此无法用傅里叶变换来表示。拉普拉斯变换是傅里叶变换的推广，拉普拉斯变换将信号从时域变换到了整个复平面，而不仅仅是虚部。拉普拉斯变换首先让信号乘以一个指数衰减的函数，使得信号绝对可积，然后再进行傅里叶变换，即：

\[X(s)=\int_{-\infty}^{\infty}x(t)e^{-\sigma t}e^{-j\Omega t}dt=\int_{-\infty}^{\infty}x(t)e^{-st}dt\]

其中$s=\sigma+j\Omega$，$\sigma$为实部，$\Omega$为虚部。$s$是复数，拉普拉斯变换可以看成是关于$s$的复变函数。

拉普拉斯变换的收敛域

当$\int_{-\infty}^{\infty}|x(t)e^{-\sigma t}|dt$绝对可积时，拉普拉斯变换收敛。拉普拉斯变换的收敛域可以分为三类：

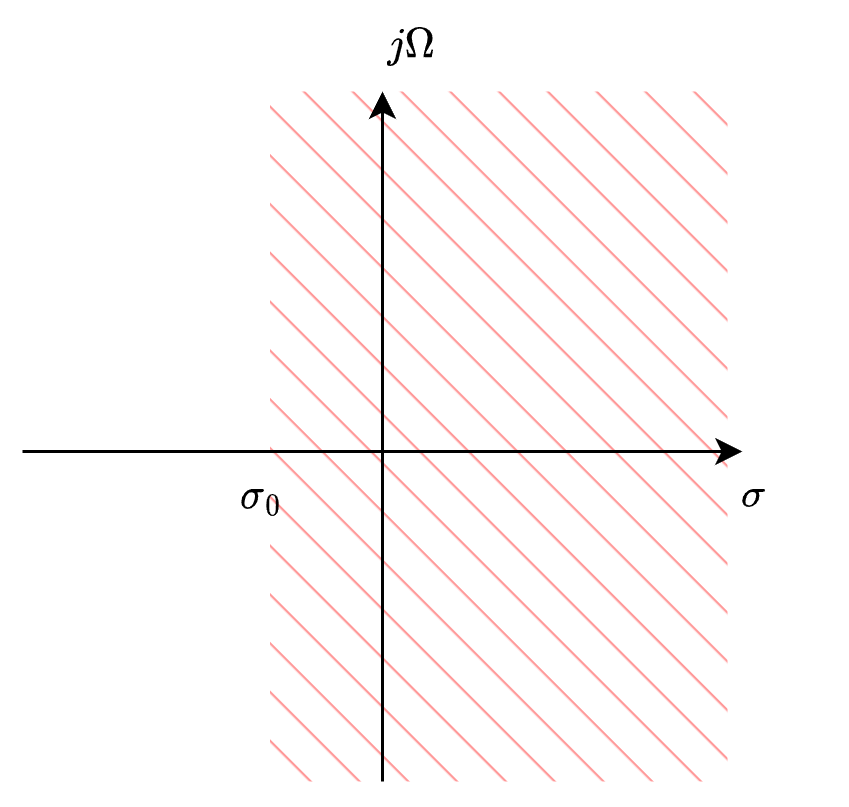
右半平面收敛：对于右边信号，$Re(s)=\sigma>\sigma_0$，$\sigma_0$为实数，$s$在右半平面，即$s$的实部大于$\sigma_0$时，拉普拉斯变换收敛。
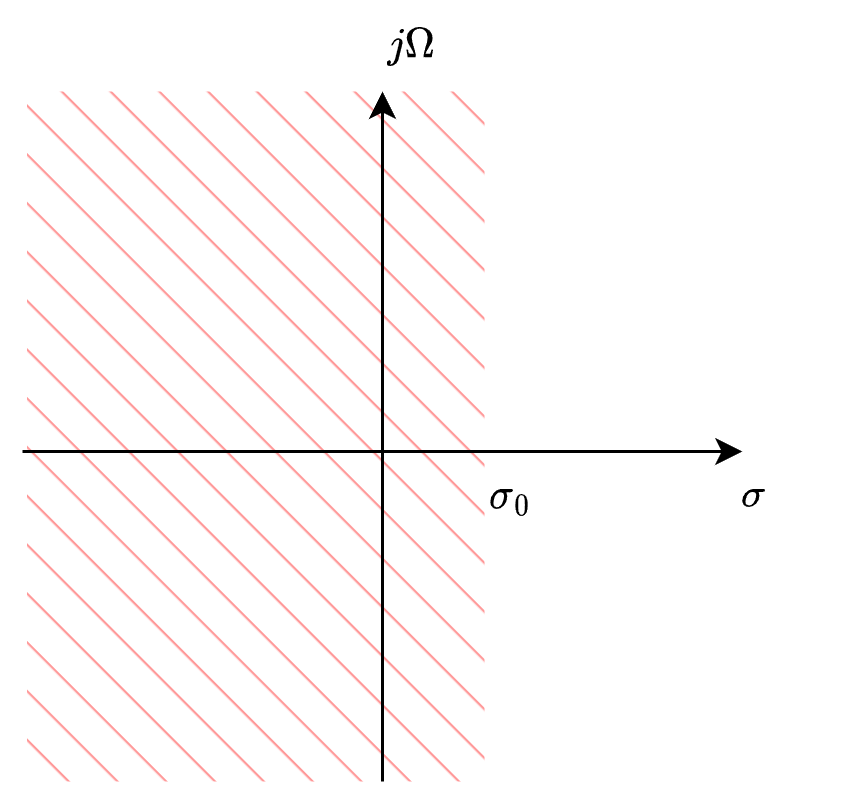
左半平面收敛：对于左边信号，$Re(s)=\sigma<\sigma_0$，$\sigma_0$为实数，$s$在左半平面，即$s$的实部小于$\sigma_0$时，拉普拉斯变换收敛。
双边收敛：对于双边信号，$\sigma_1<\sigma<\sigma_2$，$\sigma_1$和$\sigma_2$为实数，$s$在$\sigma_1$和$\sigma_2$之间，即$s$的实部在$\sigma_1$和$\sigma_2$之间时，拉普拉斯变换收敛。

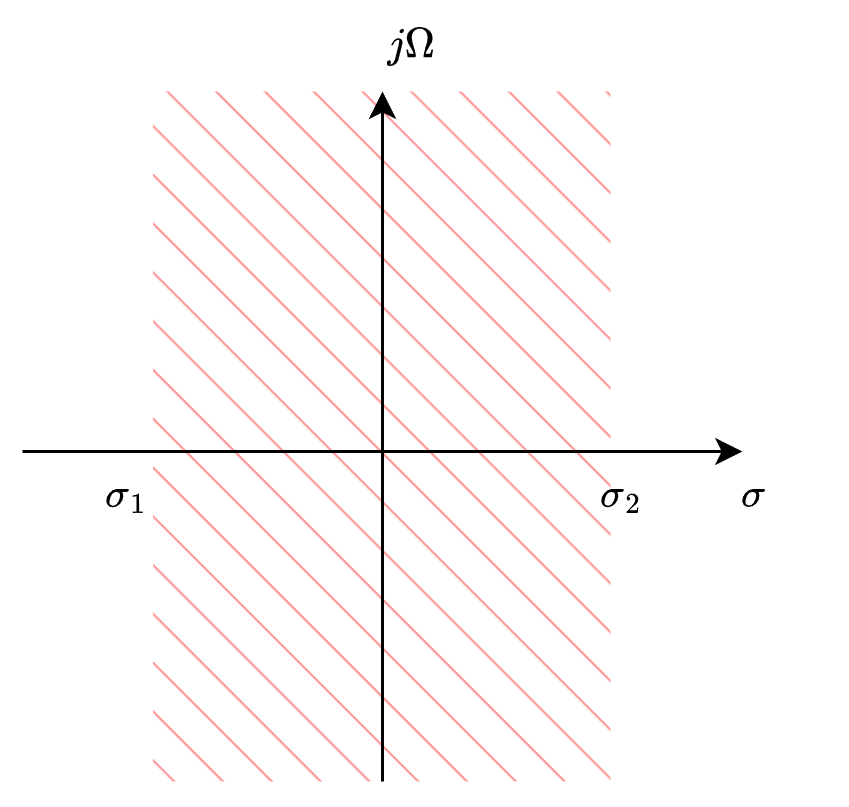
拉普拉斯变换的反变换为： $$x(t)=\frac{1}{2\pi j}\int_{\sigma-j\infty}^{\sigma+j\infty}X(s)e^{st}ds$$

拉普拉斯变换是一种数学变换，用于将连续时间信号从时间域转换到复频域，从而可以用复频域的方法来分析信号的性质。拉普拉斯变换的应用非常广泛，可以用于求解微分方程，分析连续时间线性时不变系统的稳定性。

现实中单边拉普拉斯变换应用更加广泛，原因是现实处理的信号大多是因果信号，即信号在某一时刻之前为零。在分析系统时，遇到的系统也通常是因果的系统。