#! https://zhuanlan.zhihu.com/p/669374129
模拟滤波器映射成数字滤波器的设计方法
如前所述,IIR数字滤波器的设计最常用的方法是先将对应的模拟原型滤波器设计出来,然后再将其映射成数字滤波器。这里我们介绍两种常用的映射方法:冲激响应不变法和双线性变换法。
无论使用哪种变换方法,都需要保证稳定的模拟滤波器变换成稳定的数字滤波器,即:\(s\)平面左边的极点映射到\(z\)平面单位圆内。
冲激响应不变法(impulse invariance)
引言
冲激响应不变法的核心思想是用数字滤波器的单位抽样响应去近似模拟滤波器的冲激响应,如果模拟滤波器在折叠频率以内是严格限带的,则数字滤波器的频率响应可以很好地逼近模拟滤波器的频率响应。
时域的变换关系式
模拟滤波器的冲激响应和数字滤波器的单位抽样响应之间的关系为:
\(\displaystyle h[n] = Th_c(nT)\)
其中\(T\)表示抽样间隔,\(h_c(t)\)表示模拟滤波器的冲激响应,\(h[n]\)表示数字滤波器的单位抽样响应。\(h[n]\)是\(h_c(t)\)的缩放和抽样的版本。上面关系式的证明过程如下:
连续时间信号抽样变成离散时间信号,其时域和频率关系可以分别用下面两个式子表示:
\(\displaystyle h[n] = h_c(nT)\)
\(\displaystyle H(j \Omega) = \frac{1}{T}\sum_{k=-\infty}^{\infty}H_c\left(j\Omega + jk\Omega_s\right)\)
根据离散时间傅里叶变换和傅里叶变换的关系可以得出:
\(\displaystyle H(e^{j\omega})|_{\omega=\Omega T} = H(j \Omega) = \frac{1}{T}\sum_{k=-\infty}^{\infty}H_c\left(j\frac{\omega}{T} + j\frac{2\pi k}{T}\right)\)
因此,当\(|\Omega| < \frac{\pi}{T}\)(折叠频率)时,即\(H_c(j\Omega)\)是严格限带的,则下面的关系式成立:
\(\displaystyle H(e^{j\omega}) = \frac{1}{T}H_c\left(j\frac{\omega}{T}\right),|\omega| < \pi\)
为了让\(\displaystyle H(e^{j\omega}) = H_c\left(j\frac{\omega}{T}\right)\),则时域关系式为:
\(\displaystyle h[n] = Th_c(nT)\)
变换域的变换关系式
从连续时间到离散时间的冲激响应不变法是基于时域采样来定义的,我们接下来研究从模拟系统的系统函数\(H(s)\)转化为离散时间系统的系统函数\(H(z)\)的过程。我们假定一个模拟滤波器的系统函数\(H(s)\),用单极点的形式将其展开:
\(\displaystyle H(s) = \sum_{k=1}^{N}\frac{A_k}{s - s_k}\)
其对应的冲激响应为:
\(\displaystyle h_c(t) = \sum_{k=1}^{N}A_ke^{s_kt}u(t)\)
利用冲激响应不变法,我们可以得到离散时间系统的单位抽样响应:
\(\displaystyle h[n] = Th_c(nT) = T\sum_{k=1}^{N}A_ke^{s_knT}u(n)\)
其对应的系统函数为:
\(\displaystyle H(z) = \sum_{k=1}^{N}\frac{A_k T}{1 - e^{s_kT}z^{-1}}\)
从上面的\(H(s)\)和\(H(z)\)的表达式可以看出:
\(s\)平面的极点\(s_k\)变换到\(z\)平面的极点\(z_k = e^{s_kT}\)。但是零点并没有这种变换关系。
\(H(z)\)和\(H(s)\)部分分式的系数除了比例系数\(T\)之外,是相同的,都是\(A_k\)。
如果模拟滤波器是稳定的,即极点在\(s\)平面的左半平面,则通过冲激响应不变法得出的数字滤波器也是稳定,即极点在\(z\)平面的单位圆内。
讨论
冲激响应不变法要求模拟滤波器在折叠频率以内是严格限带的,否则就会出现混叠失真。因此冲激响应不变法不适用于高通和带阻滤波器的设计。
模拟频率在折叠频率以上处衰减越大,越快,则变换后的频率响应混叠失真越小,因此通常模拟滤波器设计时会让阻带衰减超过给定的指标。
冲激响应不变法的模拟频率和数字频率之间呈线性关系,因而一个线性相位的模拟滤波器可以映射成一个线性相位的数字滤波器。对于一些对相位有线性要求的滤波器,我们可以采用冲激响应不变法来设计,比如数字微分器。
\(T\)的取值对于最终数字滤波器的设计是没有影响的,所以我们通常取\(T=1\)。
例:用冲激响应不变法设计数字巴特沃斯低通滤波器,要求频率小于\(0.2\pi\)时幅度最大衰减小于\(1dB\),频率大于\(0.3\pi\)时幅度最小衰减大于\(40dB\)。
首先将数字滤波器的参数指标转化成模拟滤波器的参数指标,利用冲激响应不变法,这里我们取\(T=1\),则模拟滤波器的参数指标如下:
通带截止频率:\(\Omega_p = 0.2\pi\) 阻带截止频率:\(\Omega_s = 0.3\pi\) 通带所允许的最大衰减:\(A_p = -20\log_{10}|H_c(j\Omega_p)|=1dB\) 阻带需要达到的最小衰减:\(A_s= -20\log_{10}|H_c(j\Omega_s)| = 40dB\)
根据给定的参数指标,设计巴特沃斯的模拟低通滤波器: 巴特沃斯的幅度平方函数如下:
\(\displaystyle |H_c(j\Omega)|^2 = \frac{1}{1+(\frac{\Omega}{\Omega_c})^{2N}}\)
因此我们可以得到下面两个方程:
\(\displaystyle {1+(\frac{\Omega_p}{\Omega_c})^{2N}} = 10^{\frac{A_p}{10}}\)
\(\displaystyle {1+(\frac{\Omega_s}{\Omega_c})^{2N}} = 10^{\frac{A_s}{10}}\)
于是求得模拟滤波器的阶次为:
\(\displaystyle N = \frac{\log_{10}(\frac{10^{\frac{A_p}{10}}-1}{10^{\frac{A_s}{10}}-1})}{2\log_{10}(\frac{\Omega_p}{\Omega_s})} = 5.8858\)
由于阶次必须为整数,所以我们取大于上式结果的最小正整数\(N=6\)。我们可以将\(N=6\)代入到上面通带或者阻带的方程来求得\(3dB\)的截至频率,如果利用通带关系式来求解,则通带指标满足,阻带指标会超过给定的,如果用阻带关系式来求解,则阻带指标刚好满足,通带指标会超过给定的。这里,我们利用冲激响应不变法,阻带衰减越大、越快,混叠失真越小,因此我们利用通带的关系式来求解,得到\(\Omega_c = 0.7032\)。
根据求得的阶次\(N=6\)和截至频率\(\Omega_c = 0.7032\),我们可以通过查表以及去归一化求得巴特沃斯模拟低通滤波器的系统函数为:
\(\displaystyle H_c(s) = \frac{0.12093}{(s^2+0.3640s+0.4945)(s^2+0.9945s+0.4945)(s^2+1.3585s+0.4945)}\)
利用冲激响应不变法,将模拟滤波器的系统函数\(H_c(s)\)变换成数字滤波器的系统函数\(H(z)\):
将\(H_c(s)\)展开成单极点的部分分式,再用冲激响应不变法的变换关系式,我们可以得到数字滤波器的系统函数为:
\(\displaystyle H(z) = \frac{0.12871-0.4466z^{-1}}{(1-1.2971z^{-1}+0.6949z^{-2})}+\frac{-2.1428+1.1455z^{-1}}{(1-1.0691z^{-1}+0.3699z^{-2})}+\frac{1.8557-0.6303z^{-1}}{(1-0.9972z^{-1}+0.2570z^{-2})}\)
这些结果的得出可以利用现成的滤波器设计软件去实现,比如matlab,python等。
验证设计出来的数字滤波器是否满足指标要求,我们画出了滤波器的幅度响应图,从图中可以看出,滤波器的通带和阻带指标都满足要求。如果不满足要求,可以通过提高滤波器的阶次来尝试着去满足要求。

双线性变换法 (bilinear transform)
引言
冲激响应不变法的缺点在于当模拟滤波器的频率高于折叠频率时会产生频率混叠失真。如果用某一函数将整个模拟滤波器的频率变换到折叠频率以内,再用\(\omega = \Omega T\)将其变换到离散时间系统的频域,就可以避免混叠失真,这种变换就是双线性变换。我们也可以从\(s\)平面到\(z\)平面的映射来研究双线性变换,因为\(s\)平面到\(z\)平面的映射是多对一的映射关系,所以产生了频率上的混叠,如果我们将整个\(s\)平面压缩到\((-\pi/T, \pi/T)\)的\(s_1\)平面,再通过\(z=e^{s_1 T}\)将\(s_1\)映射到整个\(z\)平面,这样就会使\(s\)平面与\(z\)平面是一一对应的关系,而不会产生频率混叠失真。
双线性变换的推导
将模拟滤波器的频率压缩到折叠频率以内的变换函数为:
\(\displaystyle \Omega = \tan(\frac{\Omega_1 T}{2})\)
其中\(\Omega\)表示原始模拟滤波器的频率,\(\Omega_1\)表示压缩后的频率,\(\Omega_1\)的取值范围为折叠频率以内即\((-\pi/T, \pi/T)\)。通过上面的关系式,我们接下来推导\(s\)平面到\(z\)平面的映射关系。
\(j\Omega = \frac{e^{\frac{j\Omega_1 T}{2}}-e^{-\frac{j\Omega_1 T}{2}}}{e^{\frac{j\Omega_1 T}{2}}+e^{-\frac{j\Omega_1 T}{2}}}\)
令\(s=j\Omega\)和\(s_1 = j\Omega_1\),则上面的关系式可以写成:
\(s = \frac{e^{\frac{s_1 T}{2}}-e^{-\frac{s_1 T}{2}}}{e^{\frac{s_1 T}{2}}+e^{-\frac{s_1 T}{2}}}=\frac{1-e^{-s_1 T}}{1+e^{-s_1 T}}\)
由\(s_1\)与\(z\)的关系式\(z=e^{s_1 T}\),我们可以得到:
\(s = \frac{1-z^{-1}}{1+z^{-1}}\)
模拟滤波器的角频率和数字滤波器的数字频率之间的关系为:
\(\displaystyle \Omega = \tan(\frac{\omega}{2})\)
双线性变换法通过频率轴上的非线性变换,实现了\(s\)平面到\(z\)平面的一一对应关系,从而消除了频率上的混叠失真。然而这种非线性变换(我们也称频率上的畸变)使得双线性变换法不适合设计具有线性相位要求的数字滤波器,比如数字微分器。实际上,双线性变换法适合模拟滤波器的幅频响应是分段常数型的,即低通、高通、带通、带阻这种频率选择性的滤波器。在从数字频率变换到模拟频率的过程中,我们需要利用公式\(\Omega = \tan(\frac{\omega}{2})\)将频率加以预畸运算。
双线性变换法中模拟频率\(\Omega\)和数字频率\(\omega\)是非线性的关系,通常我们会引起一个系数\(c=\frac{2}{T}\)使得在低频处,模拟频率和数字频率有近似的线性关系。因此预畸的频率关系式如下:
\(\displaystyle \Omega = \frac{2}{T}\tan(\frac{\omega}{2})\)
\(s\)和\(z\)的关系式如下:
\(\displaystyle s = \frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\)
在后面的滤波器的设计过程中,我们知道\(T\)的取值对于最终数字滤波器的设计是没有影响的,所以我们通常取\(T=2\)。也可以这样说,\(c=\frac{2}{T}\)只是用来调整数字频率和模拟频率之间的关系,对滤波器的设计并没有影响,因此这一部分都可以完全忽略掉。
例:用双线性变换法设计数字巴特沃斯低通滤波器,要求频率小于\(0.2\pi\)时幅度最大衰减小于\(1dB\),频率大于\(0.3\pi\)时幅度最小衰减大于\(40dB\)。
首先将数字滤波器的截止频率预畸为模拟滤波器的截止频率,为了计算简便,这里我们取\(T=2\),则模拟滤波器的参数指标如下:
通带截止频率:\(\Omega_p = \tan(0.1\pi)\)
阻带截止频率:\(\Omega_s = \tan(0.15\pi)\)
通带所允许的最大衰减:\(A_p = -20\log_{10}|\tan(0.1\pi)|=1dB\)
阻带需要达到的最小衰减:\(A_s= -20\log_{10}|\tan(0.15\pi)| = 40dB\)
根据给定的参数指标,设计巴特沃斯的模拟低通滤波器。
忽略了中间一些步骤,我们得出滤波器的阶次为:
\(\displaystyle N = \frac{\log_{10}(\frac{10^{\frac{A_p}{10}}-1}{10^{\frac{A_s}{10}}-1})}{2\log_{10}(\frac{\Omega_p}{\Omega_s})} = 5.305\)
由于阶次必须为整数,所以我们取大于上式结果的最小正整数\(N=6\)。这里,由于不用担心频率混叠的问题,因此我们将\(N=6\)代入到阻带的方程式来求得\(3dB\)的截至频率,阻带指标刚好满足,通带指标会超过给定的要求。
\(\displaystyle \Omega_c = \frac{\Omega_s}{10^{(\log_{10}(10^{A_s/10}-1))/2N}}=\frac{\tan{0.15\pi}}{10^{(\log_{10}(10^{1.5}-1))/12}}=0.3831\)
根据求得的阶次\(N=6\)和截至频率\(\Omega_c = 0.3831\),我们可以通过查表以及去归一化求得巴特沃斯模拟低通滤波器的系统函数为:
\(\displaystyle H_c(s) = \frac{0.0032}{(s^2+0.1998s+0.1468)(s^2+0.5418s+0.2935)(s^2+0.7401s+0.2935)}\)
利用双线性变换法,即代入\(s\)和\(z\)之间的代数关系式\(s=\frac{1-z^{-1}}{1+z^{-1}}\)将模拟滤波器的系统函数\(H_c(s)\)变换成数字滤波器的系统函数\(H(z)\): \(\displaystyle H(z)=\frac{0.0007378(1+z^{-1})^6}{(1-1.2686z^{-1}+0.7051z^{-2})(1-1.0106z^{-1}+0.3583z^{-2})(1-0.9044z^{-1}+0.2155z^{-2})}\)
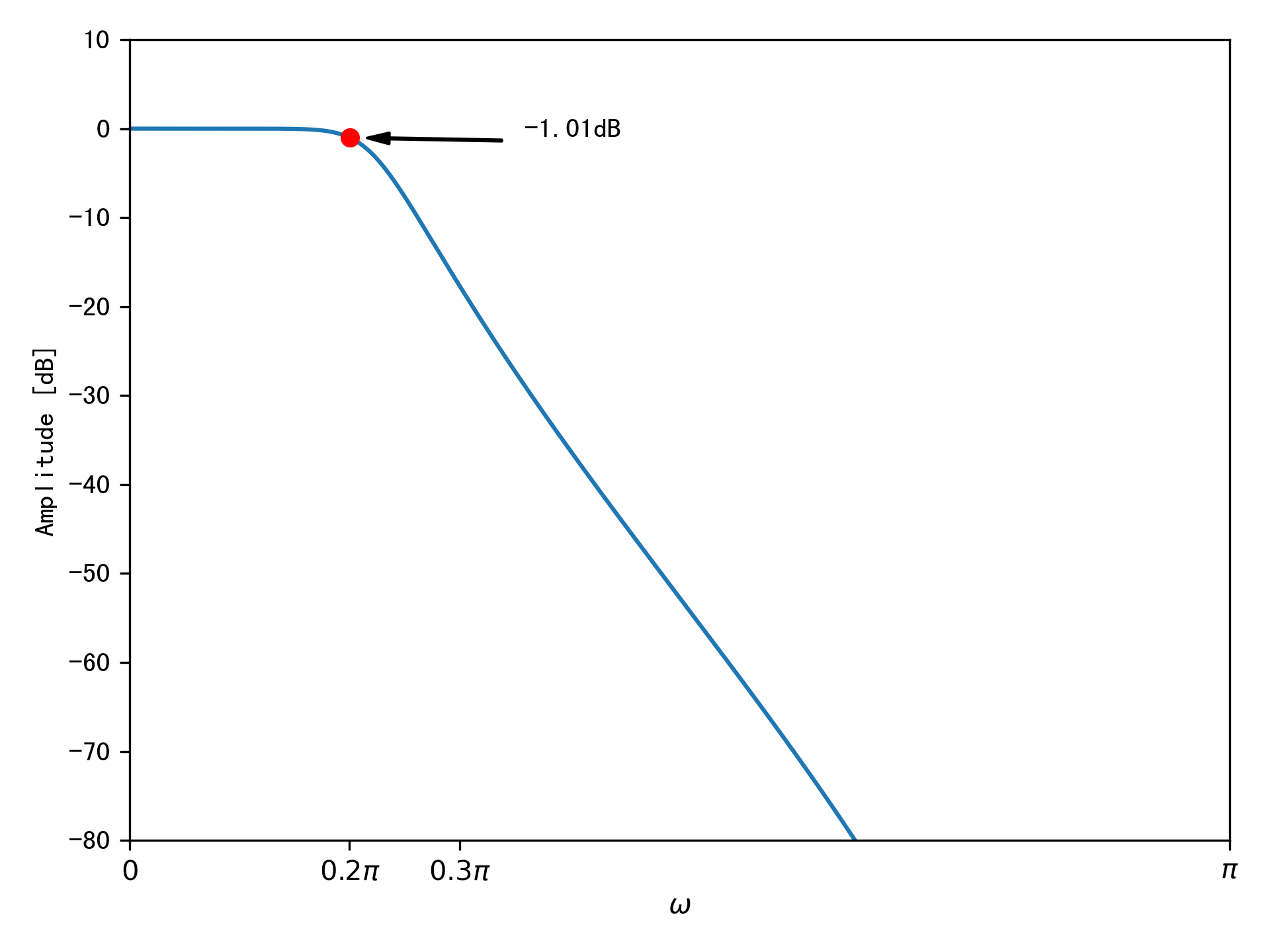
验证设计出来的数字滤波器是否满足指标要求,我们画出了滤波器的幅度响应图,从图中可以看出,滤波器的通带和阻带指标都满足要求。如果不满足要求,可以通过提高滤波器的阶次来尝试着去满足要求。
小结
冲激响应不变法和双线性变换法都是将模拟滤波器的系统函数映射到数字滤波器的系统函数的方法,这两种方法都可以用来设计IIR数字滤波器,但是它们都有各自的缺点,比如冲激响应不变法会产生频率混叠失真,双线性变换法会产生频率上的畸变。但是在频率选择性滤波器设计中,由于双线性变换法的广泛适用性,所以通常都是采用双线性变换的方法,而且在求出阶次计算关键的截止频率过程中,通常都是用阻带的关系式来求解,这一点可以在很多商用的或者开源的滤波器设计软件中得到验证。