#! https://zhuanlan.zhihu.com/p/656959103

离散时间傅里叶变换（DTFT）

引言

在信号处理中，我们经常需要将信号从时域转换到频域，这样做的好处是可以更好地分析信号的频谱特性。在连续时间信号处理中，我们可以使用傅里叶变换来实现这一目的。在离散时间信号处理中，我们可以使用离散时间傅里叶变换（DTFT）来实现这一目的。

离散时间傅里叶变换的定义

离散时间傅里叶变换（DTFT）的定义如下：

\({\displaystyle X(e^{j\omega})={\mathcal {DTFT}}\{x[n]\}=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}}\)

其反变换为：

\({\displaystyle x[n]={\mathcal {IDTFT}}\{X(e^{j\omega })\}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }X(e^{j\omega })e^{j\omega n}\,d\omega }\)

• \(\omega\)为离散时间信号的频率，是一个连续的变量，这里定义为数字频率；

• \(X(e^{j\omega})\)是关于\(\omega\)的周期函数，其周期为\(2\pi\)；

DTFT存在的条件

1. 离散时间信号\(x[n]\)绝对可和。

由于DTFT的变换公式是幂级数，因此DTFT的收敛性需要满足幂级数的收敛条件，即： \({\displaystyle |X(e^{j\omega})|=|\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}| \leq \sum _{n=-\infty }^{\infty }|x[n]||e^{-j\omega n}| \leq \sum _{n=-\infty }^{\infty }|x[n]|} < \infty\)

也就是说离散时间信号\(x[n]\)绝对可和，则\(X(e^{j\omega})\)收敛，其DTFT存在。\(x[n]\)绝对可和是离散时间傅里叶变换存在的充分条件。满足此条件，下面表达式右边的级数会一致收敛于\(X(e^{j\omega})\)。

\(\displaystyle \lim_{M \rightarrow \infty}|X(e^{j\omega})-\sum_{n=-M}^{M}x[n]e^{-j\omega n}|=0\)

所谓的一致收敛，意思就是在\(\omega\)的每个值上都收敛。

例：矩形序列的DTFT

矩形序列 \(R_N[n]\) 可以表示为：

\[\begin{split} R_N[n] = \begin{cases} 1, & \text{if } \ 0 \leq n < N \\ 0, & \text{otherwise} \end{cases} \end{split}\]

接下来，我们将计算其傅里叶变换。傅里叶变换的公式如下：

\(\displaystyle X(e^{j\omega}) = \sum_{n = -\infty}^{\infty} x[n] \cdot e^{-j\omega n}\)

将矩形序列代入公式，得到：

\(\displaystyle X(e^{j\omega}) = \sum_{n = 0}^{N-1} 1 \cdot e^{-j\omega n}\)

这是一个等比数列的求和，可以使用等比数列的求和公式来计算：

\[\begin{split}\begin{equation*} \begin{split} X(e^{j\omega}) & = \frac{1 - e^{-j\omega N}}{1 - e^{-j\omega}} \\ & = \frac{e^{-j\omega N/2}(e^{j\omega N/2} - e^{-j\omega N/2})}{e^{-j\omega/2}(e^{j\omega/2} - e^{-j\omega/2})} \\ & = e^{-j\omega(N-1)/2}\frac{\sin(\omega N/2)}{\sin(\omega/2)} \end{split} \end{equation*}\end{split}\]

这是矩形序列 \(R_N[n]\) 的傅里叶变换。请注意，它是复函数，\(X(e^{j\omega})=X_R(e^{j\omega})+X_I(e^{j\omega})=|X(e^{j\omega})|e^{j\angle{X(e^{j\omega})}}\)，其中\(|X(e^{j\omega})|\)为幅度函数或幅度谱，\(\angle{X(e^{j\omega})}\)为相位函数或相位谱。下图画出了当N=5时，矩形序列的幅度谱和相位谱。

2. 离散时间信号\(x[n]\)平方可和。

如果我们放宽一致收敛的条件，一些序列不满足绝对可和，但是满足平方可和如下： \(\displaystyle \sum _{n=-\infty }^{\infty }|x[n]|^{2}<\infty\) 则其离散时间傅里叶变换也是存在的。此时，下式右边的级数会均方收敛于离散时间傅里叶变换。 \(\displaystyle \lim_{M \rightarrow \infty}\int_{-\pi}^{\pi}|X(e^{j\omega})-\sum_{n=-M}^{M}x[n]e^{-j\omega n}|^2d \omega=0\) 换句话说，误差\(|X(e^{j\omega})-\sum_{n=-M}^{M}x[n]e^{-j\omega n}|\)不会在\(\omega\)的每个值上都趋近于0，但是其总的误差能量会趋近于0。

例：理想的数字低通滤波器 $\( H_{lp}(e^{j\omega})= \begin{cases} 1, \qquad |\omega|< \omega_c,\\ 0, \qquad \omega_c<|\omega|\leq \pi\\ \end{cases} \)$

理想的数字低通滤波器的频率响应已经给出，现在我们可以使用反变换（逆离散时间傅立叶变换）来得到其时域表达式。 为了求得时域表达式，我们可以使用反变换公式：

\(\displaystyle h_{lp}[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} H_{lp}(e^{j\omega})e^{j\omega n} d\omega\)

根据频率响应的定义，我们只需要计算积分区间在 \(|\omega| < ω_c\)内的部分。 因此，时域表达式为：

\(\displaystyle h_{lp}[n] = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c} e^{j\omega n} d\omega\)

对上述积分进行计算，可以得到：

\(\displaystyle h_{lp}[n] = \frac{1}{2\pi jn} \left(e^{j\omega_c n} - e^{-j\omega_c n}\right)=\frac{\sin\omega_c n}{\pi n}, \qquad -\infty<n<\infty\)

\(h_{lp}[n]\)不是绝对可和的，但是是平方可和的，无穷级数\(H_M(e^{j\omega})=\sum_{n=-M}^{M}\frac{\sin\omega_c n}{\pi n}e^{-j\omega n}\)不会在\(\omega\)的每个值上都一致收敛，但是会均方收敛。用级数合成的离散时间傅里叶变换和理想的数字低通滤波器的频率响应图如下：

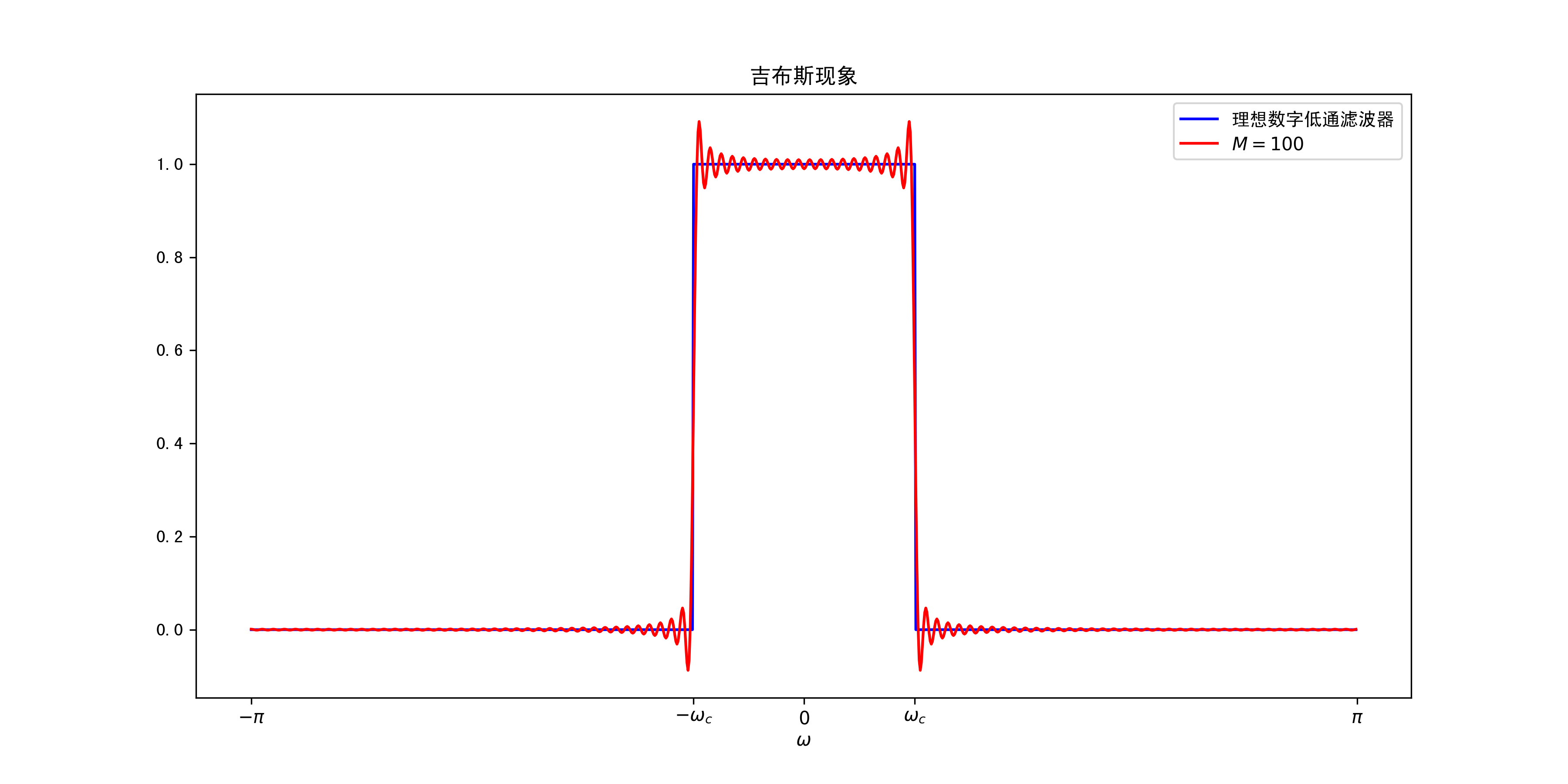
从上图可以看出，在靠近不连续点上会产生振荡，随着M的增大，振荡会越来越靠近不连续点，但是不会消失，振幅的大小不会随着M的增大而变化，这种现象称为吉布斯现象。

3. 对于一些特殊的序列（比如周期序列）既不满足绝对可和也不满足平方可和，只要引入冲激函数，其傅里叶变换也是存在的。

• 复指数序列\(x[n] = e^{j\omega_0 n}\)的离散时间傅里叶变换

\(\displaystyle \hat X(e^{j\omega}) = \sum_{i=-\infty}^{\infty}2\pi\delta(\omega-\omega_0-2\pi i)\)

• 常数序列\(x[n] = 1\)的离散时间傅里叶变换

\(\displaystyle \hat X(e^{j\omega}) = \sum_{i=-\infty}^{\infty}2\pi\delta(\omega - 2\pi i)\)

• 周期为\(N\)的抽样序列串的离散时间傅里叶变换

\(\displaystyle \hat X(e^{j\omega}) = \frac{1}{N}\sum_{i=-\infty}^{\infty}2\pi\delta(\omega - \frac{2\pi i}{N})\)

• 周期为\(N\)的周期序列\(\tilde x[n]\)的离散时间傅里叶变换

\(\displaystyle \hat X(e^{j\omega}) = \frac{1}{N}\sum_{i=-\infty}^{\infty}2\pi\delta(\omega - \frac{2\pi i}{N})\sum_{n=0}^{N-1}\tilde x[n]e^{-j\frac{2\pi n}{N}k}\)

DTFT的性质

下表列出了离散时间傅里叶变换的一些常见性质，更多的性质可以参考相关的教材。

\[\begin{split} \begin{array}{|c|c|} \hline 离散时间信号 & 离散时间傅里叶变换 \\ \hline ax_1[n] + bx_2[n] & aX_1(e^{j\omega})+ b X_2(e^{j\omega}) \\ \hline x[n-n_d] & e^{-jwn_d}X(e^{j\omega}) \\ \hline e^{j\omega_0 n}x[n] & X(e^{j(\omega-\omega_0)n}) \\ \hline x[-n] & X(e^{-j\omega}) \\ \hline nx[n] & j\frac{d X(e^{j\omega})}{d\omega} \\ \hline x[n]*h[n] & X(e^{j\omega})H(e^{j\omega}) \\ \hline x[n]h[n] & \frac{1}{2\pi}X(e^{j\omega})*H(e^{j\omega}) \quad 圆周卷积\\ \hline \end{array}\end{split}\]

• 帕塞瓦定理

  \[\sum_{n=-\infty}^{\infty}|x[n]|^2 = \frac{1}{2\pi}\int_{-\pi}^{\pi}|X(e^{j\omega})|^2d\omega\]