#! https://zhuanlan.zhihu.com/p/663449060

快速傅里叶变换（FFT）之二：Radix-2 DIF FFT

引言

在上一小节中，我们分析了Radix-2 DIT FFT的基本原理。本小节将介绍Radix-2 DIF FFT的基本原理。

基本原理

设序列\(x[n]\)的长度为\(N=2^M\)，\(M\)为整数。我们首先将\(x[n]\)分为两个长度为\(N/2\)的两个子序列。则\(x[n]\)的DFT可以表示为：

\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(k)& =\sum_{n=0}^{N-1}x[n]W_N^{nk} \\ & = \sum_{n=0}^{N/2-1}x[n]W_N^{nk} + \sum_{n=N/2}^{N-1}x[n]W_N^{nk} \\ & = \sum_{n=0}^{N/2-1}x[n]W_{N}^{nk} + \sum_{n=0}^{N/2-1}x[n+N/2]W_{N}^{(n+N/2)k} \\ & = \sum_{n=0}^{N/2-1}x[n]W_{N}^{nk} + (-1)^k\sum_{n=0}^{N/2-1}x[n+N/2]W_{N}^{nk} \\ \end{split}\end{equation*}\end{split}\]

当\(k=2r\)为偶数时，\((-1)^k=1\)，当\(k=2r+1\)为奇数时，\((-1)^k=-1\)。因此，我们可以将\(X(k)\)分为两部分：

\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(2r)& = \sum_{n=0}^{N/2-1}x[n]W_{N}^{n2r} + \sum_{n=0}^{N/2-1}x[n+N/2]W_{N}^{n2r} \\ & = \sum_{n=0}^{N/2-1}(x[n]+x[n+N/2])W_{N/2}^{nr} \end{split}\end{equation*}\end{split}\]

\[\begin{split}\displaystyle \begin{equation*} \begin{split} X(2r+1)& = \sum_{n=0}^{N/2-1}x[n]W_{N}^{n(2r+1)} - \sum_{n=0}^{N/2-1}x[n+N/2]W_{N}^{n(2r+1)} \\ & = \sum_{n=0}^{N/2-1}(x[n]-x[n+N/2])W_N^nW_{N/2}^{nr} \end{split}\end{equation*}\end{split}\]

我们可以用下面的示意图表示上述的过程：

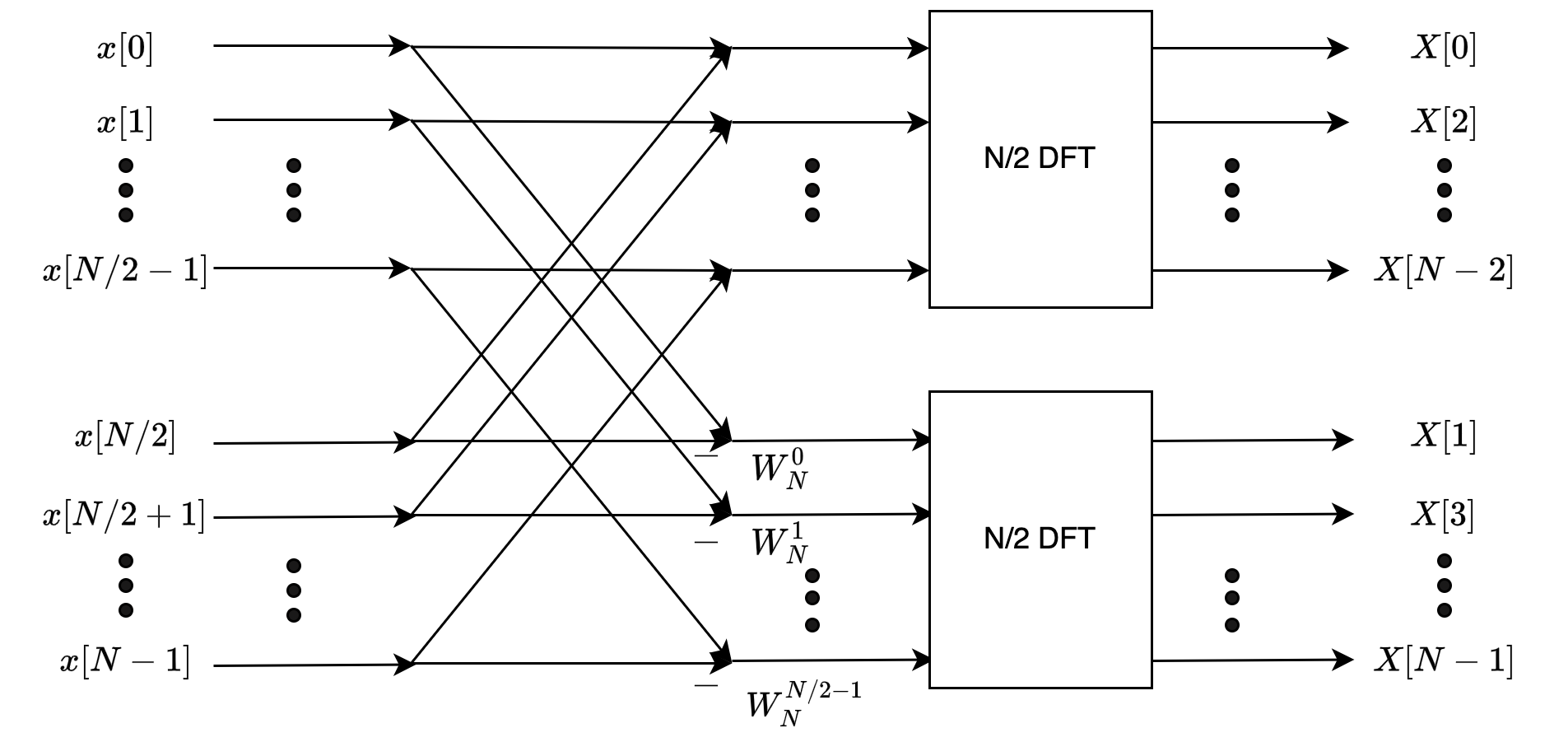
其中\(X[2r]\)是\(x[n]+x[n+N/2]\)的\(N/2\)点的DFT，\(X[2r+1]\)是\((x[n]-x[n+N/2])W_N^n\)的\(N/2\)点的DFT。我们可以按着这种思想继续将\(x[n]+x[n+N/2]\)和\((x[n]-x[n+N/2])W_N^n\)分为两个长度为\(N/4\)的子序列，然后再进行蝶形运算。直到最后的序列为2点的DFT。我们以8点的DFT为例，画出了Radix-2 DIF FFT的计算流程图：

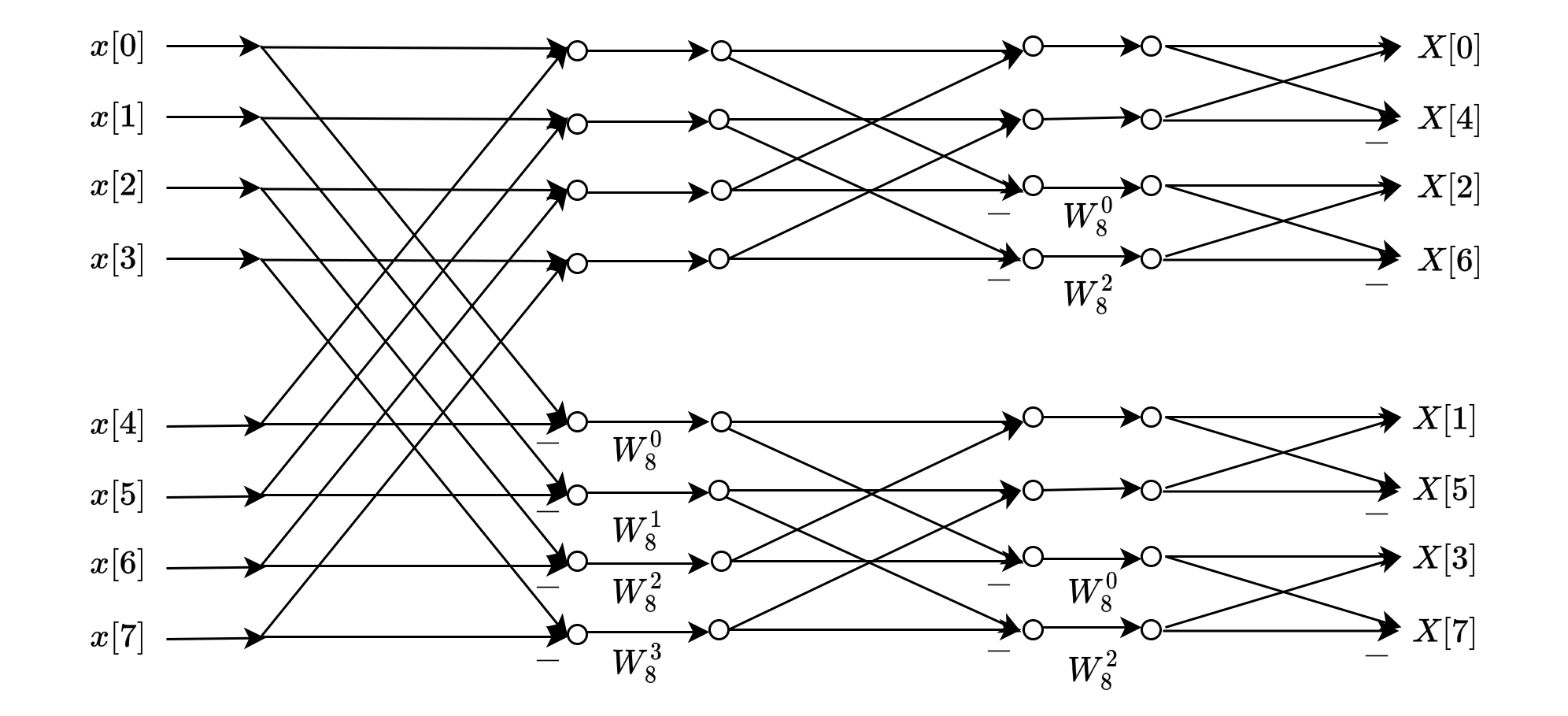
DIF和DIT的比较

DIF时域的输入为自然顺序，频域的输出为倒位序。DIT时域的输入为倒位序，频域的输出为自然顺序。DIF和DIT的基本蝶形结构是互为转置的。因此，DIF和DIT的流图是互为转置的。按照转置定理，两个流图的输入-输出特性必然相同。转置就是将流图的所有支路方向都反向，并且交换输入与输出，但节点变量值不交换。因此DIF的计算复杂度跟DIT也是一样的。