#! https://zhuanlan.zhihu.com/p/669524770

高通、带通、带阻IIR数字滤波器的设计

这一小节我们简单描述数字高通，带通，带阻IIR数字滤波器的设计过程，我们只分析商用的滤波器设计软件和Python的Scipy库中最常用的设计方法和步骤。其具体的设计步骤如下图所示：

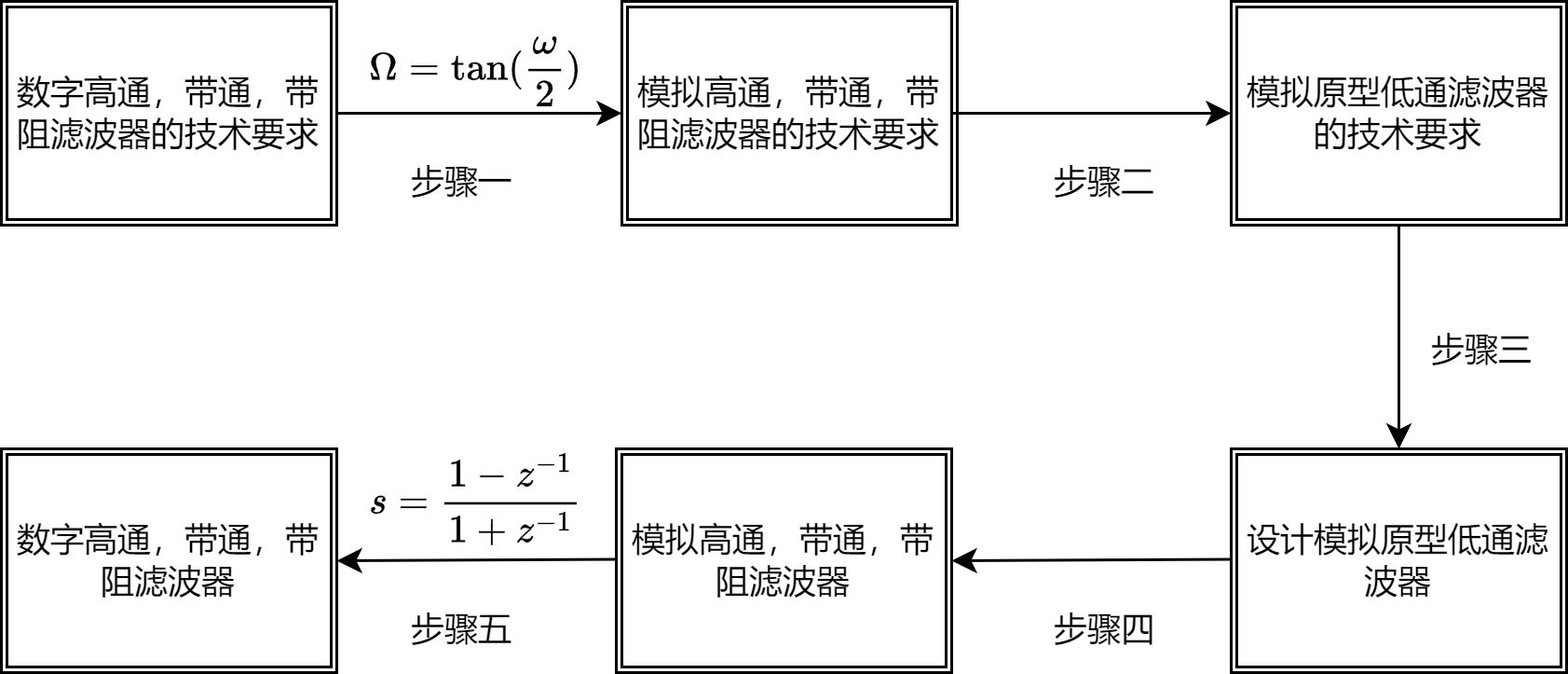
其中步骤二中从模拟高通、带通、带阻滤波器导出模拟原型低通滤波器的阻带截至频率如下表所示：

\[\begin{split} \begin{array}{|c|c|} \hline 数字滤波器类型 & 模拟原型滤波器的阻带频率 \\ \hline 高通 & {\Omega_p}/{\Omega_s} \\ \hline 带通 & |\frac{\Omega_s^2-\Omega_u\Omega_l}{\Omega_s(\Omega_u-\Omega_l)} | \\ \hline 带阻 & |\frac{\Omega_s(\Omega_u-\Omega_l)}{\Omega_s^2-\Omega_u\Omega_l}| \\ \hline \end{array}\end{split}\]

这里，我们假定了通带截止频率的归一化，也就是说模拟原型低通滤波器的通带截止频率为1。\(\Omega_s\)表示数字滤波器的阻带截止频率，\(\Omega_u\)表示数字滤波器的带通上截止频率，\(\Omega_l\)表示数字滤波器的带通下截止频率。

步骤四中的模拟频带的变换关系如下表所示：

\[\begin{split}\begin{array}{|c|c|} \hline 数字滤波器类型 & 频带变换关系式 \\ \hline 高通 & {\Omega_p}/{s} \\ \hline 带通 & \frac{s^2+\Omega_u\Omega_l}{(\Omega_u-\Omega_l)s} \\ \hline 带阻 & \frac{(\Omega_u-\Omega_l)s}{s^2+\Omega_u\Omega_l} \\ \hline \end{array}\end{split}\]

我们弄清楚基本原理之后，可以使用Matlab的Signal Processing toolbox和Python的Scipy库来设计数字滤波器。

在接下来的例子中，我们利用了python的Scipy库中的iirdesign函数来设计数字滤波器，滤波器系统函数的结果我们用sos的方式来表示。

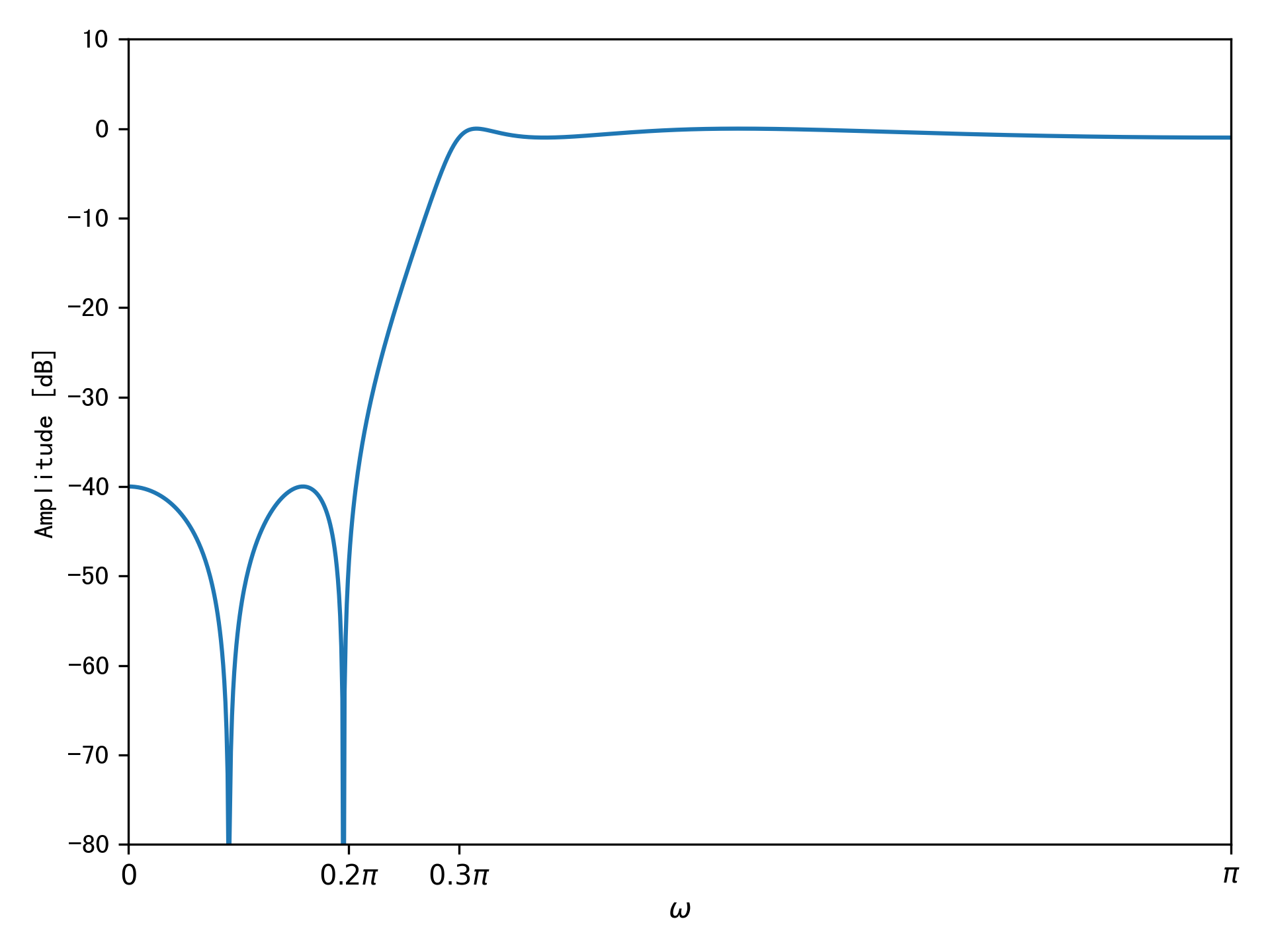
例：设计一个IIR数字高通滤波器，要求频率小于\(0.2\pi\)时幅度最小衰减大于\(40dB\)，频率大于\(0.3\pi\)时幅度最大衰减小于\(1dB\)。

设计代码如下：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 性能指标要求
ws = 0.2
wp = 0.3
gpass = 1
gstop = 40

# 设计数字高通滤波器，其中模拟滤波器为椭圆型滤波器，映射方式为双线性变换
system = signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='sos')
np.savetxt('./data/hp1.txt', system)
# 绘制滤波器的幅度响应
w, h = signal.sosfreqz(system, worN=np.linspace(0, np.pi, 1000))
plt.plot(w, 20 * np.log10(abs(h)))
plt.xlabel(r'$\omega$')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.xlim([0, np.pi])
plt.ylim([-80, 10])
plt.xticks([0, 0.2*np.pi, 0.3*np.pi, np.pi],
         [r'$0$', r'$0.2\pi$', r'$0.3\pi$', r'$\pi$'])

plt.tight_layout()

plt.savefig('./images/hp1.png', dpi=300)

plt.show()

滤波器的幅度响应如下图：

系统函数如下：

\(\displaystyle H(z)= \frac{0.2668-0.5117z^{-1}+0.2668z^{-2}}{1-0.2058z^{-1}+0.2520z^{-2}} \frac{1-1.6356z^{-1}+z^{-2}}{1-1.0823z^{-1}+0.8428z^{-2}}\)

例：设计一个IIR数字带通滤波器，带通的截止频率分别为\(0.2\pi\)和\(0.5\pi\)，阻带截止频率分别为\(0.1\pi\)和\(0.6\pi\)，通带所允许的最大衰减为\(1dB\)，阻带所允许的最小衰减为\(40dB\)。

设计代码如下：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

wp = [0.2, 0.5]
ws = [0.1, 0.6]
gpass = 1
gstop = 40

system = signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='sos')

np.savetxt('./data/bp1.txt', system)

w, h = signal.sosfreqz(system, worN=np.linspace(0, np.pi, 1000))

plt.plot(w, 20 * np.log10(abs(h)))

plt.xlabel(r'$\omega$')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.xlim([0, np.pi])
plt.ylim([-80, 10])
plt.xticks([0, 0.1*np.pi, 0.2*np.pi, 0.5*np.pi, 0.6*np.pi, np.pi],
         [r'$0$', r'$0.1\pi$', r'$0.2\pi$', r'$0.5\pi$', r'$0.6\pi$', r'$\pi$'])

plt.tight_layout()

plt.savefig('./images/bp1.png', dpi=300)

plt.show()

滤波器的幅度响应如下图：

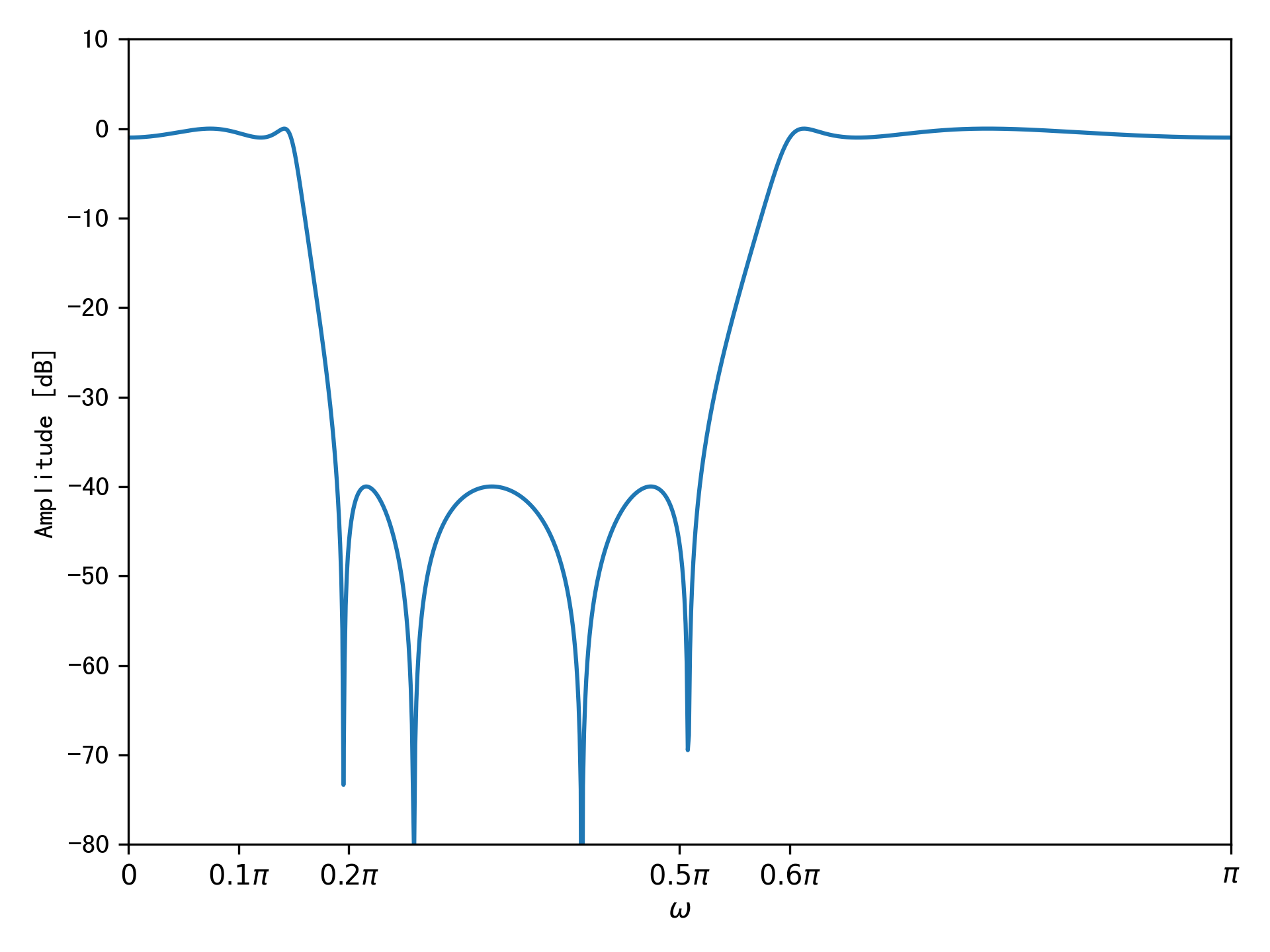
例：设计一个IIR数字带阻滤波器，带通的截止频率分别为\(0.1\pi\)和\(0.6\pi\)，阻带截止频率分别为\(0.2\pi\)和\(0.5\pi\)，通带所允许的最大衰减为\(1dB\)，阻带所允许的最小衰减为\(40dB\)。

设计代码如下：

import numpy as np
from scipy import signal
import matplotlib.pyplot as plt

wp = [0.1, 0.6]
ws = [0.2, 0.5]
gpass = 1
gstop = 40

system = signal.iirdesign(wp, ws, gpass, gstop, analog=False, ftype='ellip', output='sos')

np.savetxt('./data/bs1.txt', system)
w, h = signal.sosfreqz(system, worN=np.linspace(0, np.pi, 1000))

plt.plot(w, 20 * np.log10(abs(h)))

plt.xlabel(r'$\omega$')
plt.ylabel('Amplitude [dB]')
plt.margins(0, 0.1)
plt.xlim([0, np.pi])
plt.ylim([-80, 10])
plt.xticks([0, 0.1*np.pi, 0.2*np.pi, 0.5*np.pi, 0.6*np.pi, np.pi],
         [r'$0$', r'$0.1\pi$', r'$0.2\pi$', r'$0.5\pi$', r'$0.6\pi$', r'$\pi$'])

plt.tight_layout()
plt.savefig('./images/bs1.png', dpi=300)
plt.show()

滤波器的幅度响应如下图：