#! https://zhuanlan.zhihu.com/p/656390044

离散时间系统的描述

如前所述，一个离散时间系统可以用下面的框图表示：

当系统是线性时不变的，系统的输出等于系统的输入与系统的单位抽样响应的卷积和。即： $\displaystyle y(n) = x(n) * h(n)$ ，其中$h(n)$为系统的单位抽样响应。

系统函数

系统函数定义为系统单位抽样响应的Z变换：

$\displaystyle H(z) = \mathcal{Z}\{h(n)\} = \sum_{n=-\infty}^{\infty}h(n)z^{-n}$

系统输入的Z变换与系统函数的乘积等于系统输出的Z变换，即：

$\displaystyle Y(z) = H(z)X(z)$

$\displaystyle H(z) = \frac{Y(z)}{X(z)}$

因果性：一个线性时不变系统是因果的，则$h[n]=0,n<0$，其系统函数的收敛域必须大于某一半径。
稳定性：一个线性时不变系统是稳定的，则$h[n]$绝对可和，即$\sum_{n=-\infty}^{\infty}|h[n]|<\infty$，其系统函数的收敛域包括单位圆。

如果一个线性时不变系统是因果稳定的，则其系统函数的收敛域$|z|>R,\text{其中}R<1$，也就是说收敛域大于某一半径，这个半径小于1，也意味着系统的全部极点必须在单位圆内。

系统的频率响应

系统的频率响应定义为单位抽样响应的离散时间傅里叶变换：

$\displaystyle H(e^{j\omega}) = \mathcal{DTFT}\{h(n)\} = \sum_{n=-\infty}^{\infty}h(n)e^{-j\omega n}$

系统输出的频率响应等于系统输入的频率响应与系统频率响应的乘积，即：

$\displaystyle Y(e^{j\omega}) = H(e^{j\omega})X(e^{j\omega})$

$\displaystyle H(e^{j\omega}) = \frac{Y(e^{j\omega})}{X(e^{j\omega})}$

通常系统的频率响应$H(e^{j\omega})$在每一个$\omega$的取值上都是一个复数，由实部和虚部组成，其模值为系统的幅度响应，即系统增益，其幅角为系统的相位。

$\displaystyle H(e^{j\omega}) = Re\{H(e^{j\omega})\}+Im\{H(e^{j\omega})\}$

$\displaystyle H(e^{j\omega}) = |H(e^{j\omega})|e^{j\angle H(e^{j\omega}) }$

其中，$|H(e^{j\omega})|$为系统的幅度响应（也称为幅度谱），$\angle H(e^{j\omega})$为系统的相位响应（也称为相位谱）。信号进入系统后，系统会给信号带来幅度失真和相位失真。

复数的相位角并不是唯一的，可以在相位角上添加任何2π的整数倍而不影响复数的值。当使用反正切进行数值计算相位时，通常会得到相位的主值。我们将$H(e^{j\omega})$的相位主值表示为$\textrm{ARG}\{H(e^{j\omega})\}$，其取值在$(-\pi, \pi]$之间，即 $\displaystyle -\pi < \textrm{ARG}\{H(e^{j\omega})\} \leq \pi$

任何能给出函数$H(e^{j\omega})$正确复数值的其他角度，都可以用主值表示为： $\displaystyle \angle H(e^{j\omega})=\textrm{ARG}\{H(e^{j\omega})\}+2\pi \gamma(\omega)$

其中$\gamma(\omega)$可以在每个$\omega$值处取不同的正整数或负整数。

在很多情况下，作为$\omega$的函数来看，$\textrm{ARG}\{H(e^{j\omega})\}$会出现不连续性，我们称为“包裹”(wrapped phase)相位，因为模2π的计算可以看作是将相位包裹在一个圆上。另外，$\textrm{ARG}\{H(e^{j\omega})\}$可以被“展开”(unwrapped phase)成一个在$\omega$上连续的相位曲线。连续（展开）相位曲线表示为$\textrm{arg}\{H(e^{j\omega})\}$。

群延迟（group delay）：群延迟是相位响应对频率的导数的负值。

\[ \tau_g(\omega) = -\frac{d\angle H(e^{j\omega})}{d\omega}\]

群延迟失真（group delay distortion）：群延迟失真是指群延迟随频率的变化而变化，导致不同频率的信号在系统中的传输时间不同，从而导致信号的失真。也称为时间弥散（time dispersion)。

下图表示了群延迟失真对于信号的影响，输入信号是由三个频点$(0.2\pi, 0.5\pi, 0.8\pi)$窄带信号组成的宽带信号，经过全通系统后，由于不通频点的群延迟不同，导致了不同频点的信号经过系统后会产生不同的时间延迟，从而引起了不同频点信号的重叠，产生了失真。

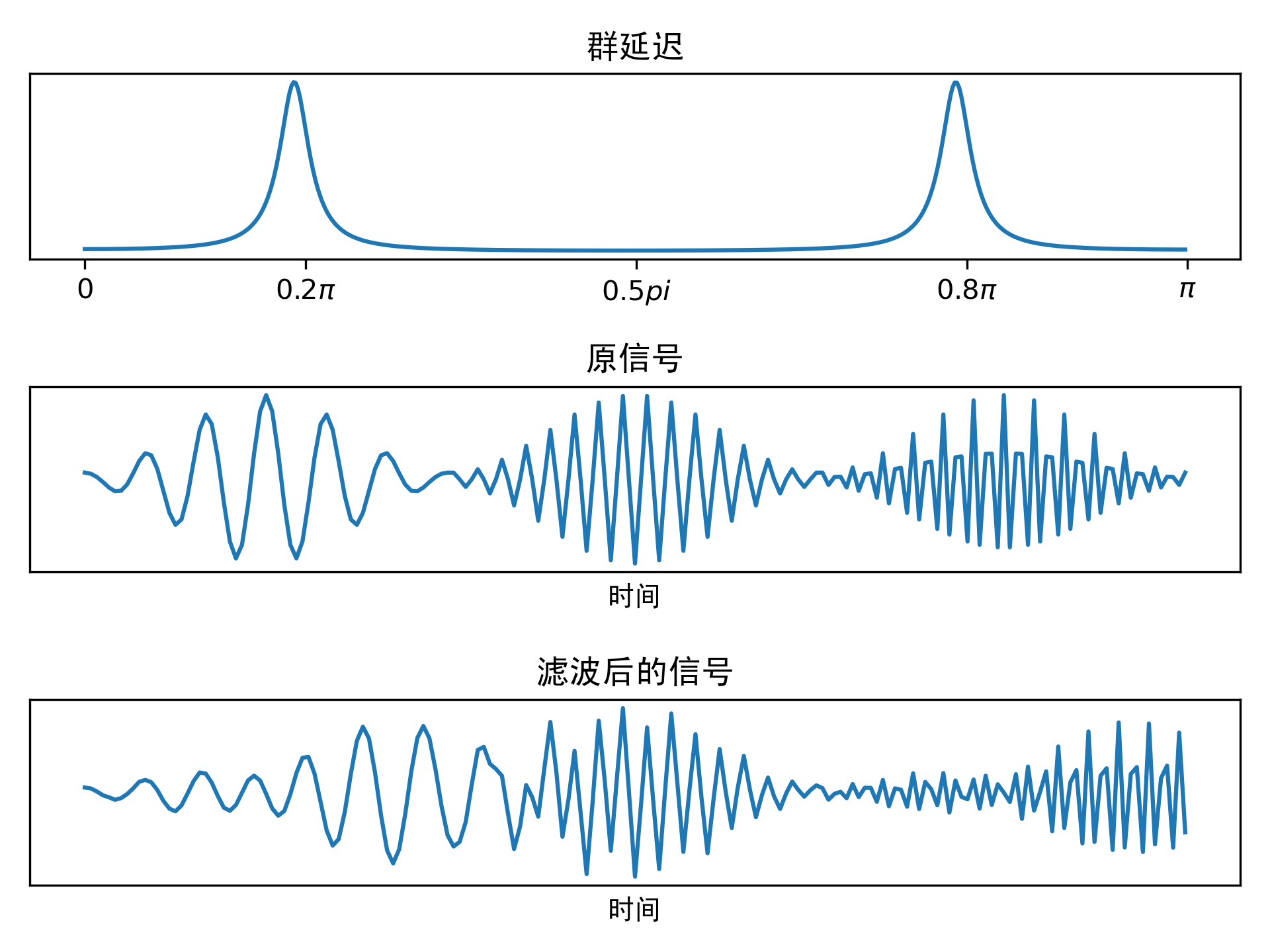
线性相位：当相位响应是关于$\omega$的线性函数时，即$\phi(\omega)=\beta+\alpha \omega$，即群延迟为常数，此时的相位称为线性相位。系统具有线性相位时，它对于输入信号的影响，只是将输入信号在时域上引入了固定的时延。

在数据传输和图像传输系统中，相位失真通常对系统的影响很大，理论上最好的方式是相位响应为0，这样就没有相位上的失真，但实际系统中，如果相位为零，就意味着信号时域必须偶对称，偶对称必然造成系统是非因果的，因此是不可实现的。通常在实际系统中，我们要求系统是线性相位的，即相位响应为线性函数，也就是说群延迟为某一常数，这样就可以保证不同频率的信号具有相同的传输时间延迟，从而避免了群延迟失真。线性相位的相位失真只是让信号在时域上引入了固定的时延，在系统其他部分，可以通过引入相应的时延来补偿。

常系数的线性差分方程

对于一个常系数的线性差分方程，其形式为：

$\displaystyle y(n) = \sum_{k=1}^{N}a_ky(n-k) + \sum_{m=0}^{M}b_mx(n-m)$

当满足初始松弛条件时，即系统的初始转态为0时，系统是因果的，此时利用Z变换，可以求解系统的输出如下：

$\displaystyle Y(z) = \frac{\sum_{m=0}^{M}b_mz^{-m}}{1-\sum_{k=1}^{N}a_kz^{-k}}X(z)$

$\displaystyle H(z) = \frac{Y(z)}{X(z)} = \frac{\sum_{m=0}^{M}b_mz^{-m}}{1-\sum_{k=1}^{N}a_kz^{-k}}$

对$H(z)$的分母和分子进行因式分解，可以得到： $\displaystyle H(z) = K\frac{\prod_{m=1}^{M}(1-c_mz^{-1})}{\prod_{k=1}^{N}(1-d_kz^{-1})}$

其中，$K$为常数，$c_m$为系统函数的零点和$d_k$为系统函数的极点。

极点通常与函数的分母的因子相关联，当分母为零时，就会导致函数在某些点处出现极点。例如，对于有理函数（分子和分母都是多项式的函数），分母的根（使分母等于零的点）通常对应于函数的极点。零点通常与函数的分子的因子相关联，当分子为零时，函数的值为零。对于有理函数，分子的根（使分子等于零的点）通常对应于函数的零点。

用$z=e^{j\omega}$代入$H(z)$，可以得到系统的频率响应：

$\displaystyle H(e^{j\omega}) = K\frac{\prod_{m=1}^{M}(1-c_me^{-j\omega})}{\prod_{k=1}^{N}(1-d_ke^{-j\omega})}$

其幅度响应为：

$\displaystyle |H(e^{j\omega})| = |K|\frac{\prod_{m=1}^{M}|1-c_me^{-j\omega}|}{\prod_{k=1}^{N}|1-d_ke^{-j\omega}|}$

其相位响应为：

$\displaystyle \angle H(e^{j\omega}) = \angle K + \sum_{m=1}^{M}\angle(1-c_me^{-j\omega}) - \sum_{k=1}^{N}\angle(1-d_ke^{-j\omega})$

线性时不变系统的特征函数$e^{j\omega n}$

当系统的输入$x[n]=e^{j\omega n}$时，系统的输出

\[\begin{split} \begin{align*} y[n] & = \sum_{m=-\infty}^{\infty}x[n-m]h[m] \\ & = \sum_{m=-\infty}^{\infty}e^{j\omega(n-m)}h[m] \\ & = e^{j\omega n}\sum_{m=-\infty}^{\infty}h[m]e^{-j\omega m} \\ & = e^{j\omega n}H(e^{j\omega}) \end{align*} \end{split}\]

我们定义系统的特征函数为$e^{j\omega n}$，系统的特征值为$H(e^{j\omega})$（系统的频率响应）。从上面的推导可以看出当系统输入为复指数序列时，系统的输出是系统的输入乘以系统的频率响应，系统的频率响应不会改变系统输入的频率，只会对系统输入的幅度和相位产生失真。

例：正弦序列$x[n]=A\cos(\omega_0n+\phi)$经过一个线性时不变系统，求其输出。解： $$

\[\begin{align*} x[n] & =A\cos(\omega_0n+\phi) \\ & = \frac{A}{2}(e^{j(\omega_0n+\phi)}+e^{-j(\omega_0n+\phi)}) \\ & = \frac{A}{2}e^{j\phi}e^{j\omega_0n}+ \frac{A}{2}e^{-j\phi}e^{-j\omega_0n} \\ \end{align*}\]

$$

$\displaystyle y[n]=H(e^{j\omega_0})\frac{A}{2}e^{j\phi}e^{j\omega_0n}+H(e^{-j\omega_0})\frac{A}{2}e^{-j\phi}e^{-j\omega_0n}$

由于$x[n]$是实序列，因此$H(e^{-j\omega_0})=H^*(e^{j\omega_0})$，于是可以得到

$\displaystyle y[n]=A|H(e^{j\omega})|\cos\{\omega_0 n+\phi+\angle H(e^{j\omega})\}$

对于正弦序列或者复指数序列，系统不会改变其频率，只会影响其幅度值和相位值。

可逆系统

给定一个线性时不变系统，其系统函数为$H(z)$，如果存在一个系统函数$H_i(z)$，使得$H(z)H_i(z)=1$，则称系统存在可逆的系统。

对应可逆系统的系统函数$H_i(z)$也可以用下面的式子表示：

$\displaystyle H_i(z) = \frac{1}{H(z)}$

可逆系统的频率响应为：

$\displaystyle H_i(e^{j\omega}) = \frac{1}{H(e^{j\omega})}$

时域上，如果系统是可逆的，则存在一个系统的单位抽样序列$h_i(n)$，使得$h(n)*h_i(n)=\delta(n)$，其中$\delta(n)$为单位抽样序列。

一个系统是可逆的，要求该系统的所有极点和零点都在单位圆内。也就是该系统是最小相位系统。最小相位系统我们会在后面的章节中详细讨论。

离散时间系统的描述

系统函数

系统的频率响应

常系数的线性差分方程

线性时不变系统的特征函数\(e^{j\omega n}\)

可逆系统