#! https://zhuanlan.zhihu.com/p/660932539
DFT变换应用之一(频谱分析)
DFT变换最重要的一个应用是做信号的频谱分析,这一小节以正弦信号做频谱分析为例,说明DFT变换在频谱分析中的应用。实际中很多信号都可以由很多正弦信号所组成,所以正弦信号是非常有代表性的一种信号。
我们重点分析了加窗截断对频谱分析的影响,以及频率分辨力的概念。
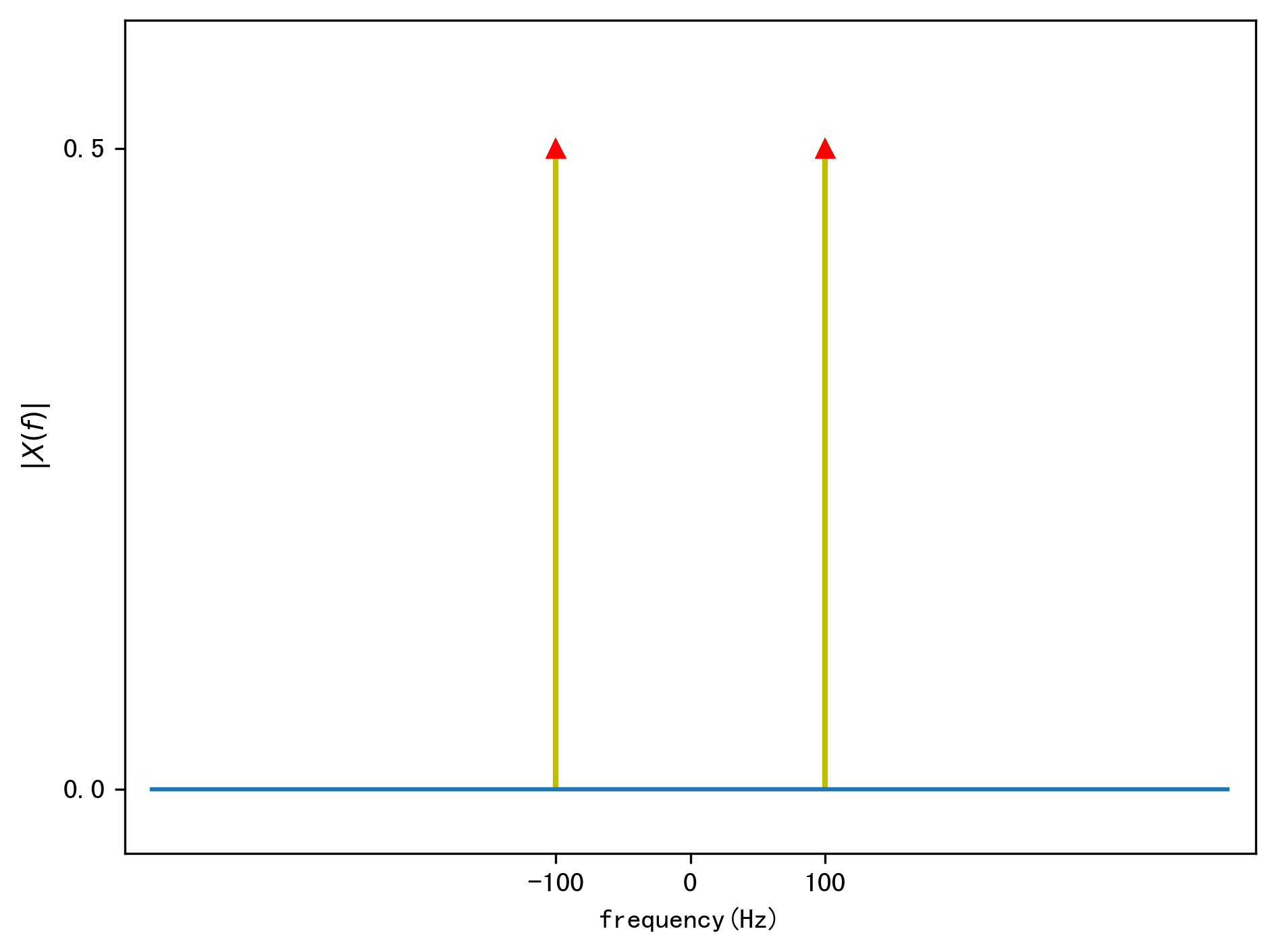
给定一个余弦信号\(x(t) = cos(2\pi*100 t)\),我们利用DFT变换对其进行频谱分析。该信号时域和频域图如下:

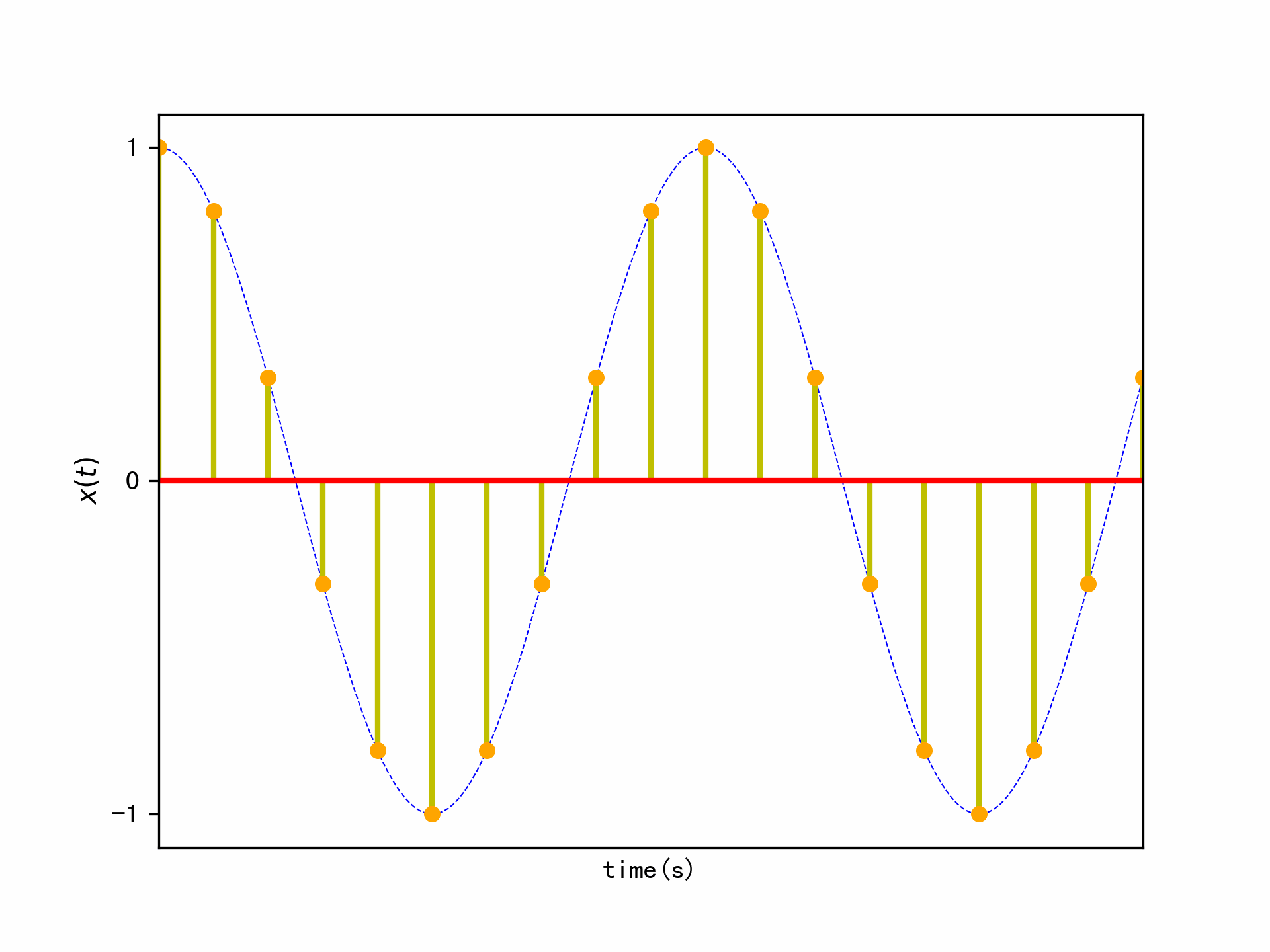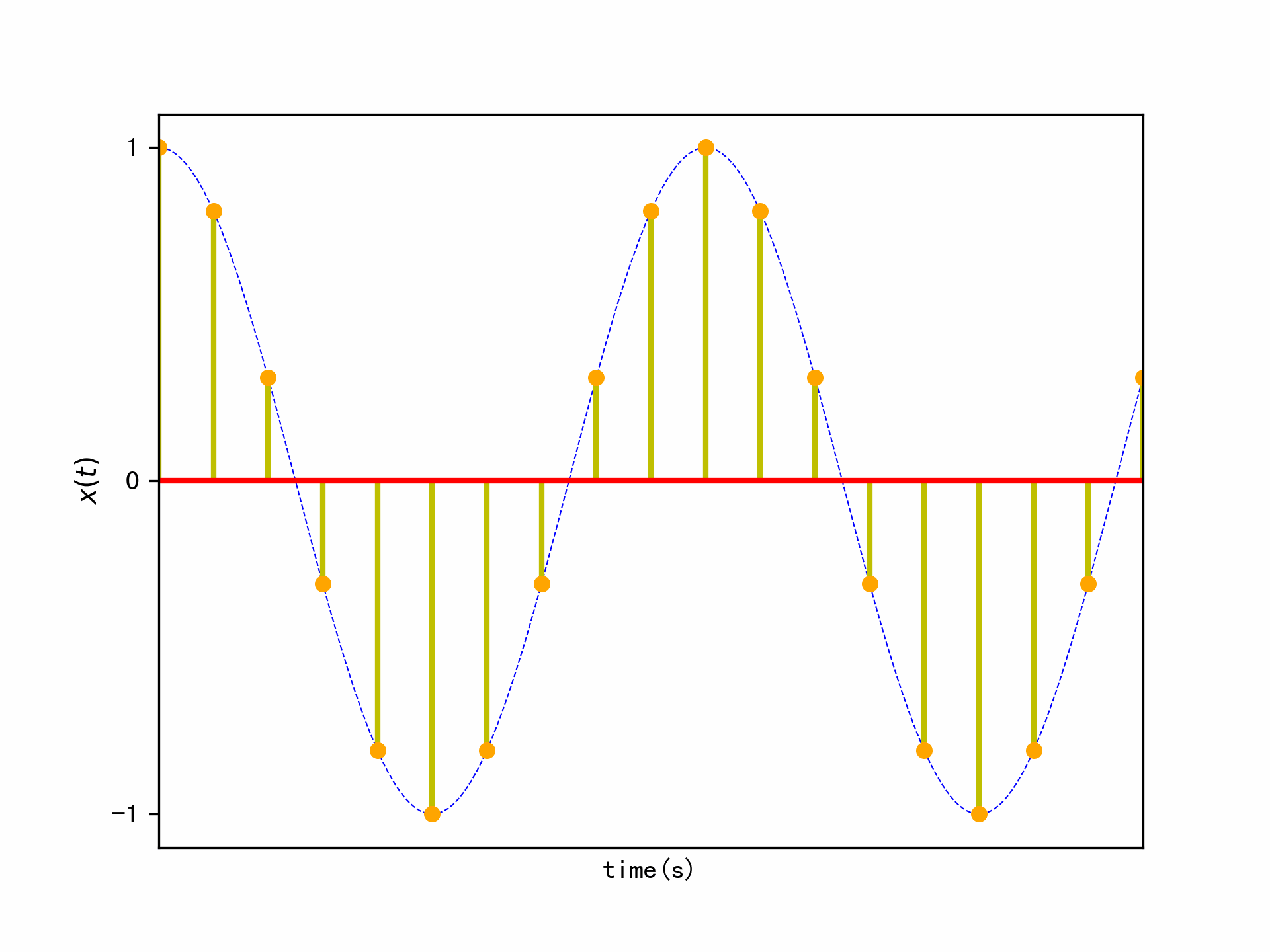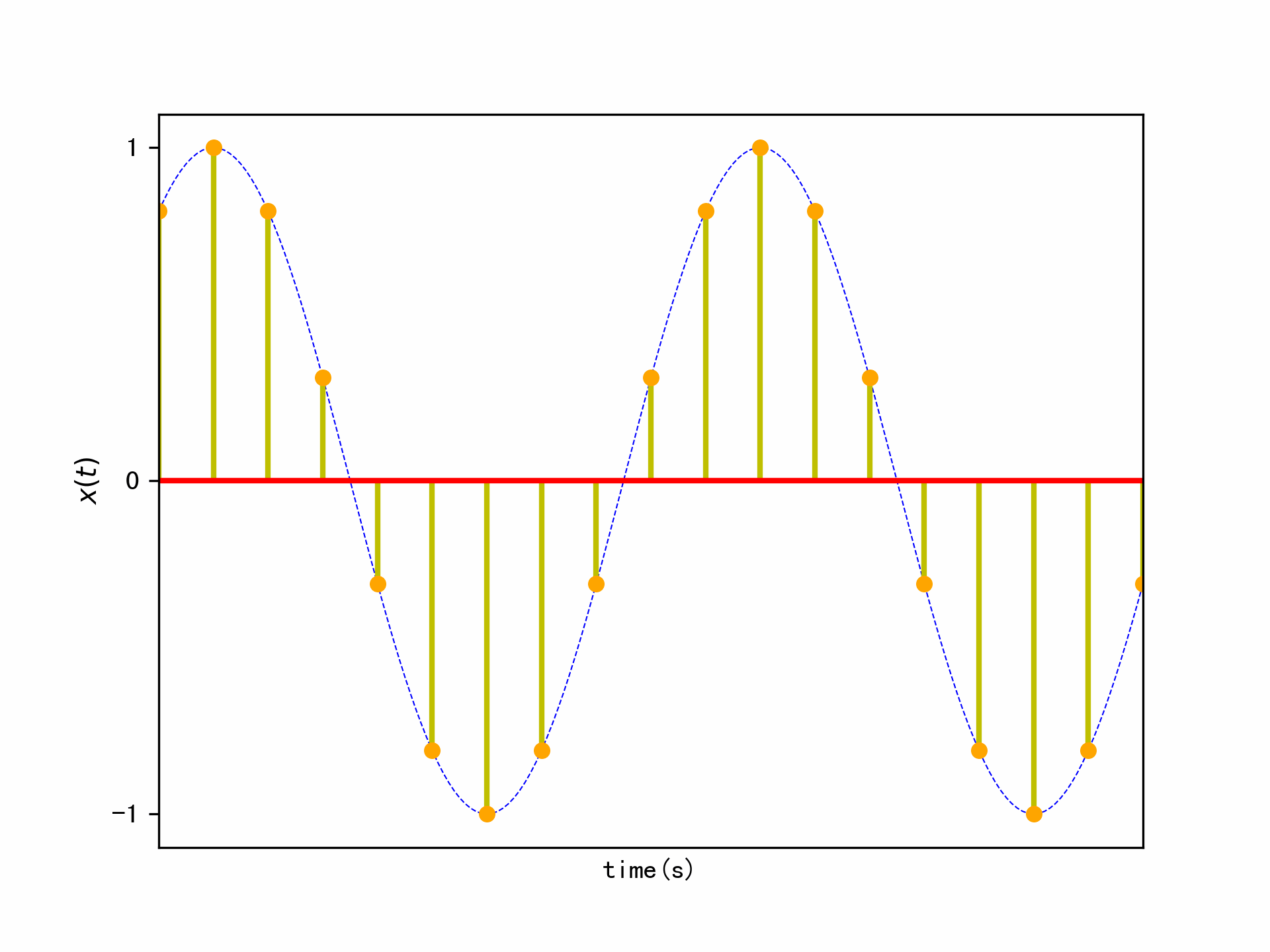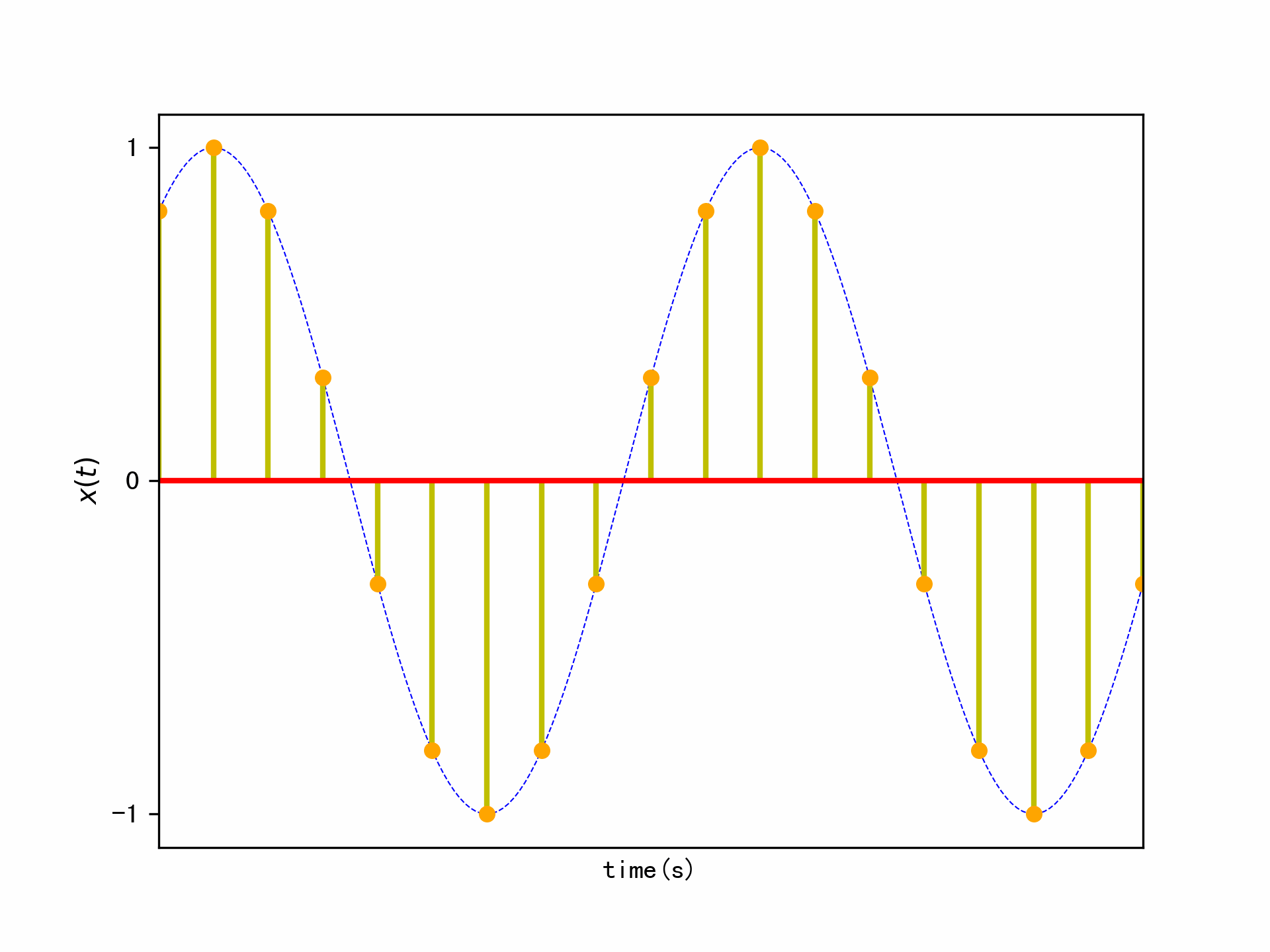
首先进行时域的抽样,抽样必须满足抽样定理,即抽样频率\(f_s\)必须大于信号的最高频率\(f_1\)的两倍,即\(f_s > 2f_1\),这里我们取\(f_s = 1000Hz\)为信号最高频率的10倍,时域的抽样示意图如下:
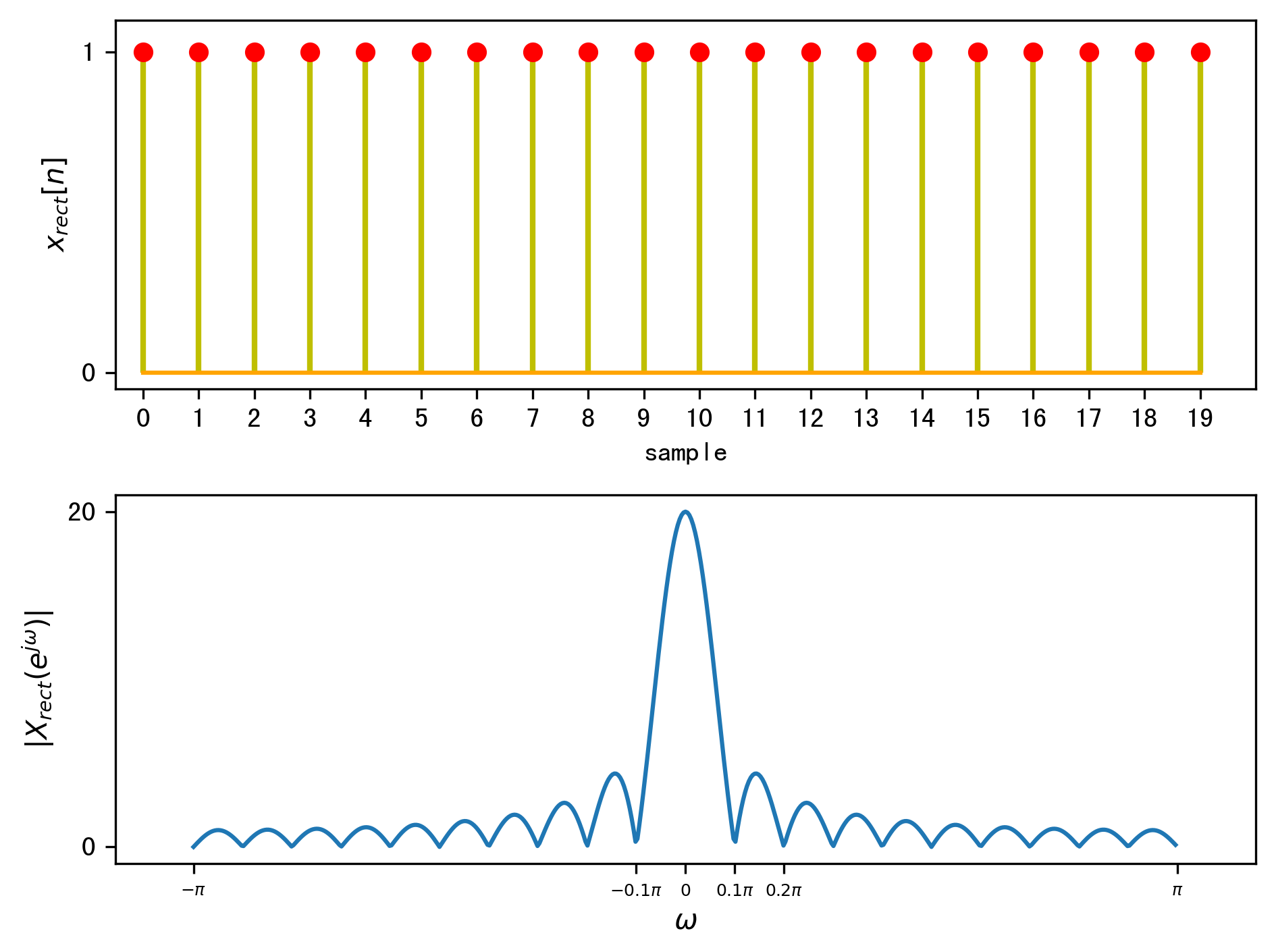
为了说明DFT变换用于谱分析会遇到的一些问题,我们截取了非常短的信号长度即0.02秒,这样信号的抽样点数为\(N=20\)。信号在时域的直接截断,相当于信号在时域乘上了一个矩形窗函数。我们先来回顾一下矩形窗函数的时域和频域图:
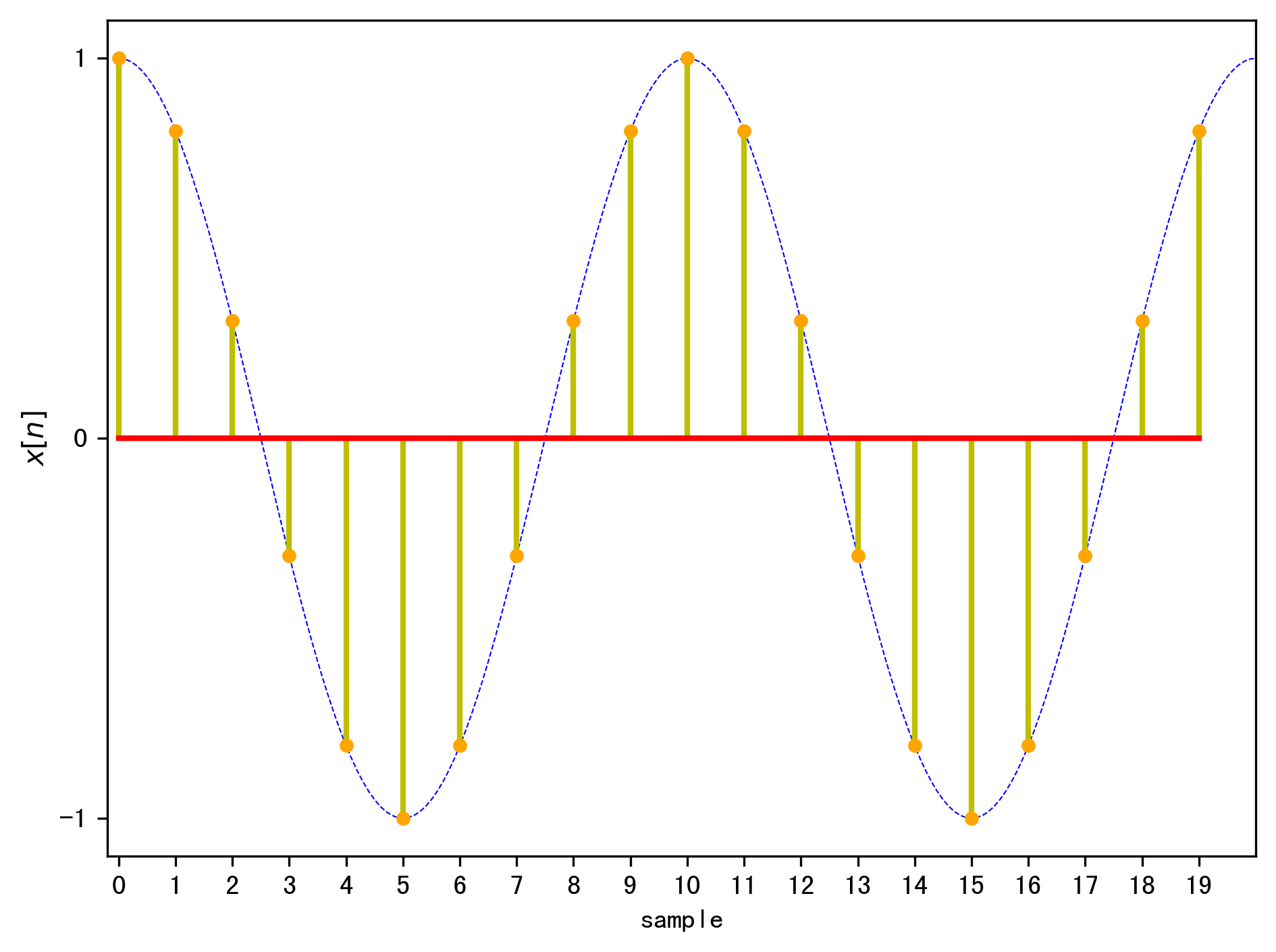
信号加矩形窗后的时域图如下:
两个信号在时域上相乘,在频域上为两个信号的卷积,因此信号在频域上会加宽,产生拖尾,造成对临近频率的干扰(这种现象叫频谱泄漏。时域直接截断后,信号频域如下图所示:
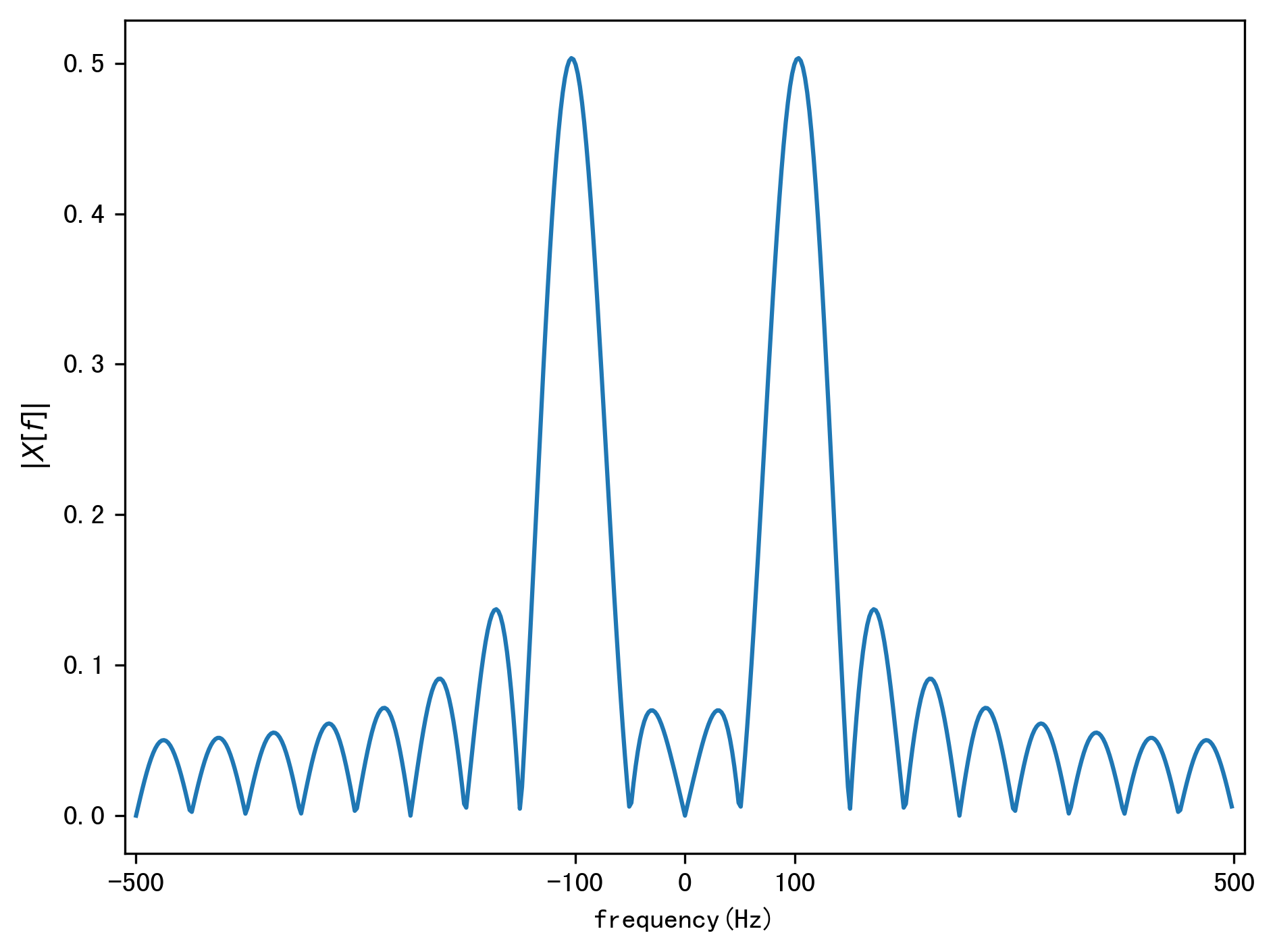
如果截断的信号长度刚好是信号周期的整数倍,那么频域上那些离散的频率点\(k f_s/N, \quad k=0, \ldots, N-1\),除了在信号频率\(\pm f_1\)处有幅度为\(1/2\)的峰值,其他频率点的幅度都为0,这样看上去就不存在频率泄露。
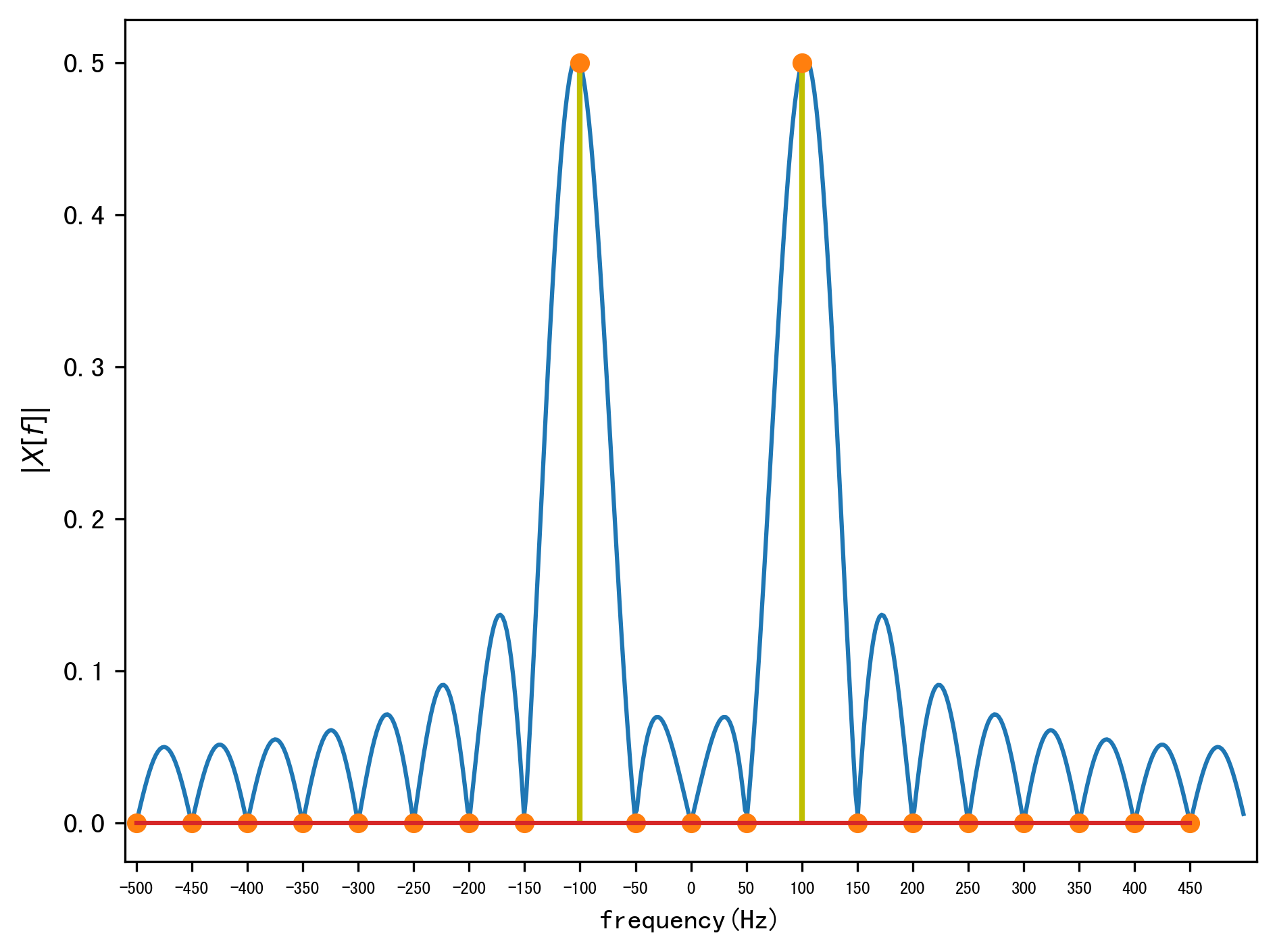
但是在实际应用中,由于进入系统的信号可能由多个周期信号组成,我们很难知道信号的周期,因此很难保证截断的信号长度刚好是信号周期的整数倍,频谱泄漏是不可避免的。假定我们截断的信号长度为\(N=26\),此时截取的长度不再是周期信号的整数倍,信号频域如下图所示:
从图中可以看出离散频率点为\(\frac{f_s}{26}k\),此时信号存在严重的频谱泄漏,要减少频谱泄漏,可以采取以下两种方式:
加旁瓣衰减更快的窗函数;
增加信号截断的长度,即增加采样点的个数。
以下我们列出了三种窗函数的时域和频域图:

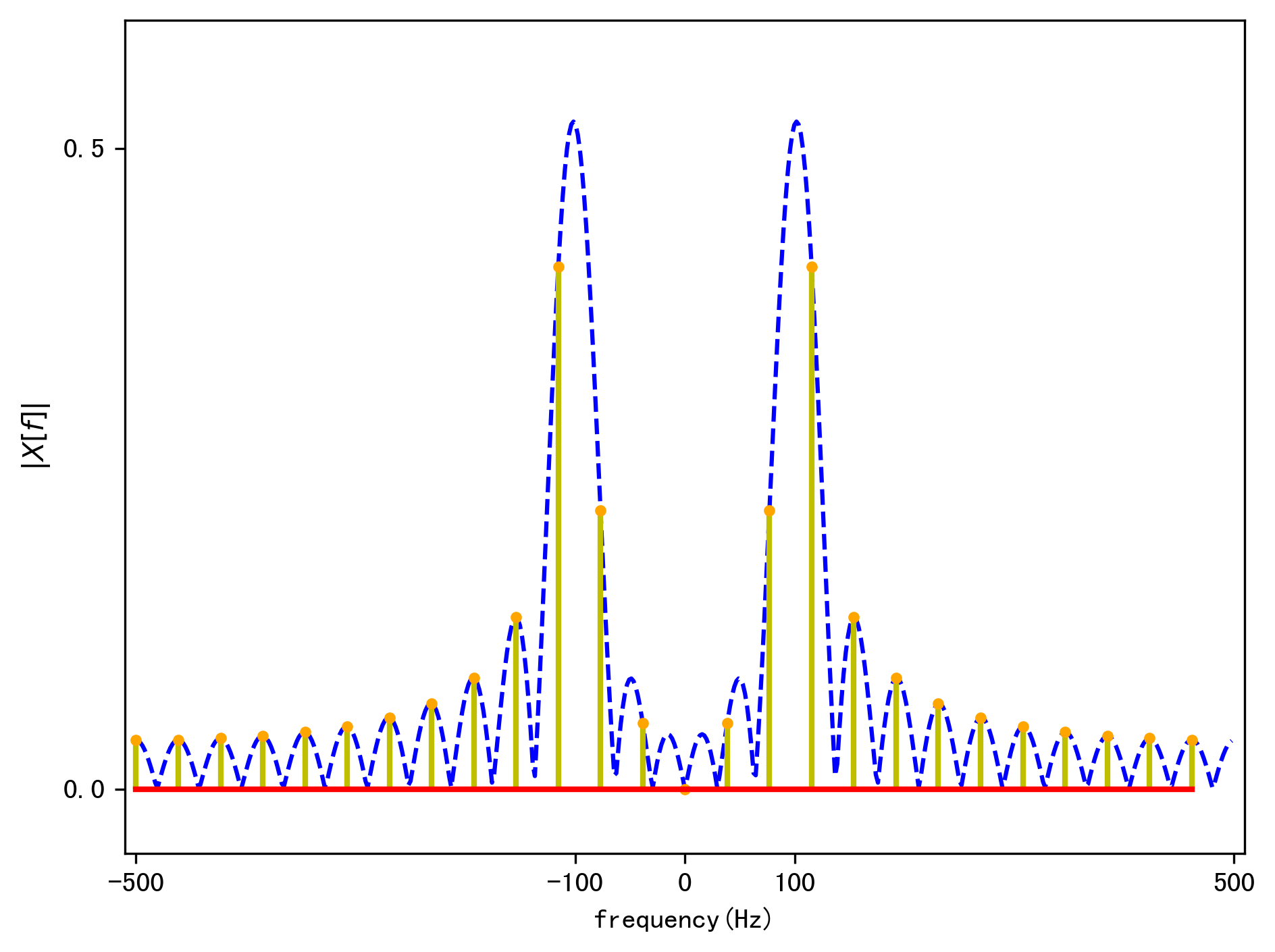
为了改善频谱泄漏,我们用衰减更快的hann窗对信号进行截断,截断后的信号频域图如下:
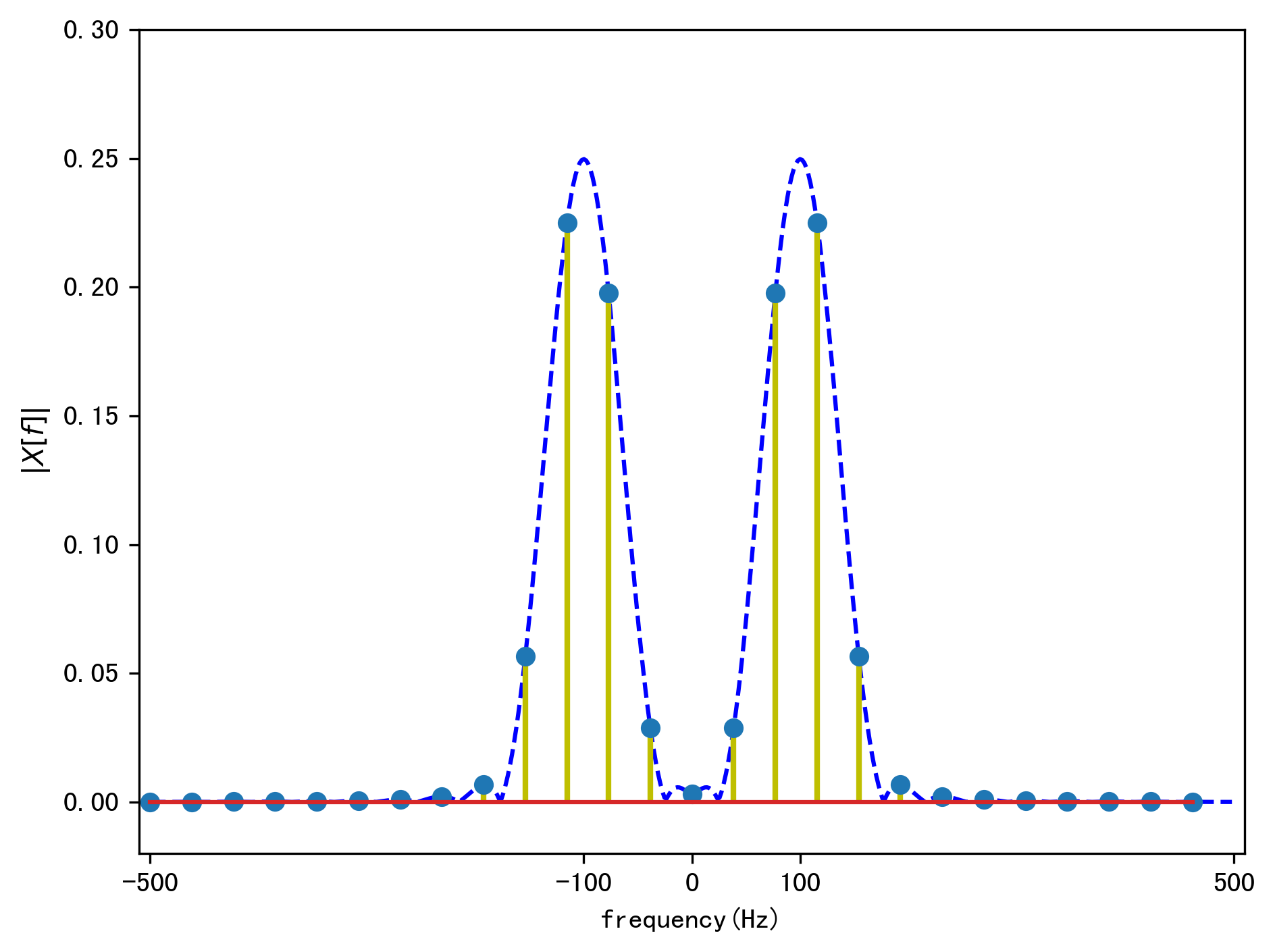
从图中可以看到频谱泄漏有所减少,但是信号的主瓣宽度增加了,我们可以通过增加信号的长度来减少主瓣宽度。下面我们将信号的长度增加到\(N=64\),此时信号的频域如下图所示:
可以看到信号的主瓣宽度减小了,频率分辨力会得到提高。频率分辨力定义为分辨两个信号频率的能力。一个简单的例子说明,如果两个信号的频率相差很小,那么在频域上就很难分辨这两个信号,因为它们的频谱会重叠在一起,如果两个信号的频率相差很大,那么在频域上就很容易分辨这两个信号,因为它们的频谱不会重叠在一起。频率分辨力的定义为两个信号频率之差的最小值,即\(\Delta f_{min}\),频率分辨力越大,说明信号频率之间的分辨能力越强。频率分辨力的计算公式为:
其中\(T_M\)为信号的实际长度(补零不算),也就是说频率分辨力只跟信号的实际长度有关。\(T_M = N/F_s\),\(N\)为信号的时域采样点数,\(f_s\)为信号的采样频率。因此信号的频率分辨力也可以定义为:
\(\Delta f_{min}\)越小,信号的频率分辨力越大,说明信号的频谱分辨率越高,可以分辨的频率越多。
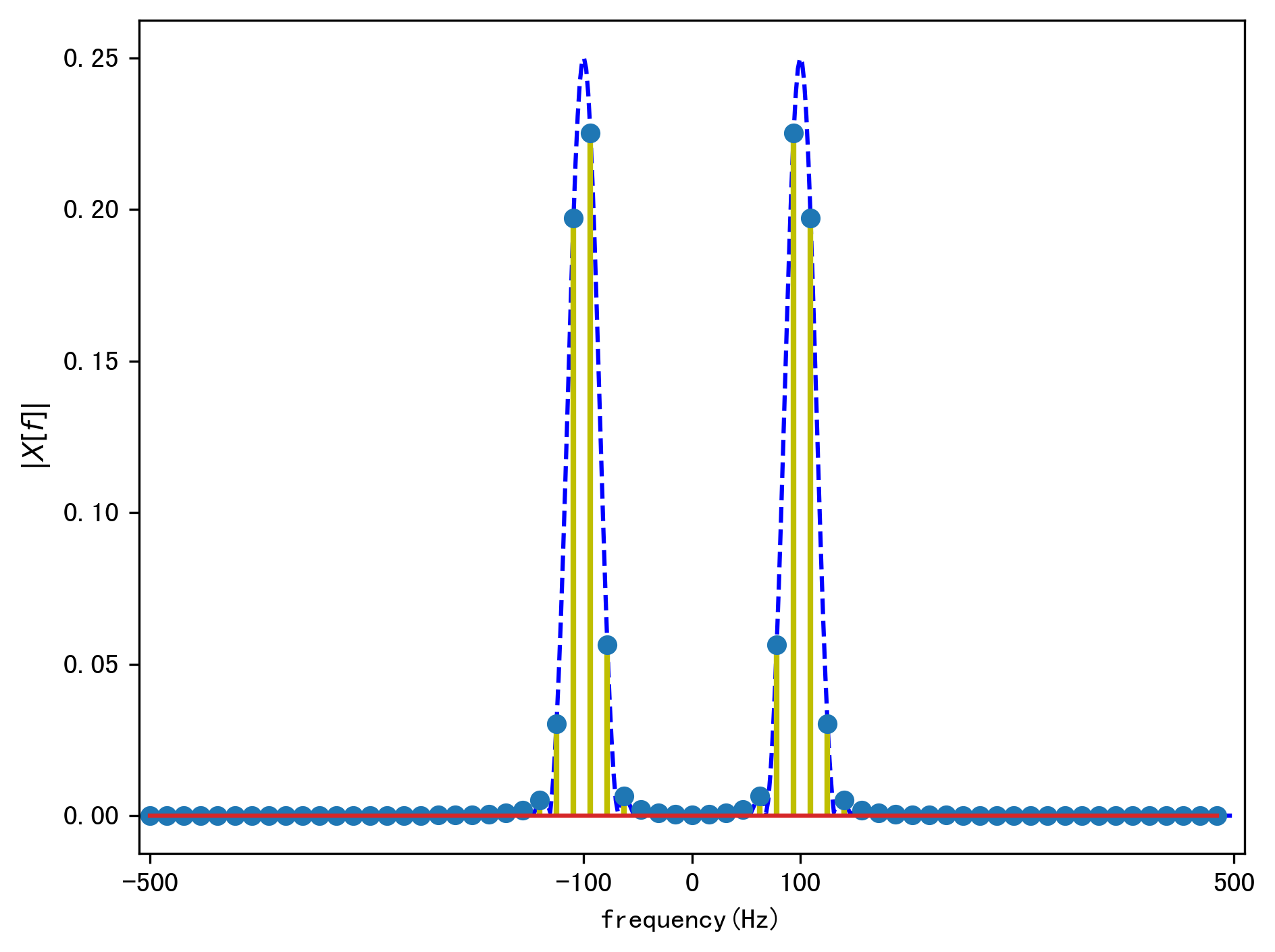
例:给定一个正弦信号:\(x(t) = cos(2\pi*100 t) + 0.5cos(2\pi *120t)\),在时域上截取多少长度可以在频域将这两个信号分辨出来?
当时域上截取的信号足够长时,该信号的频域如下图:
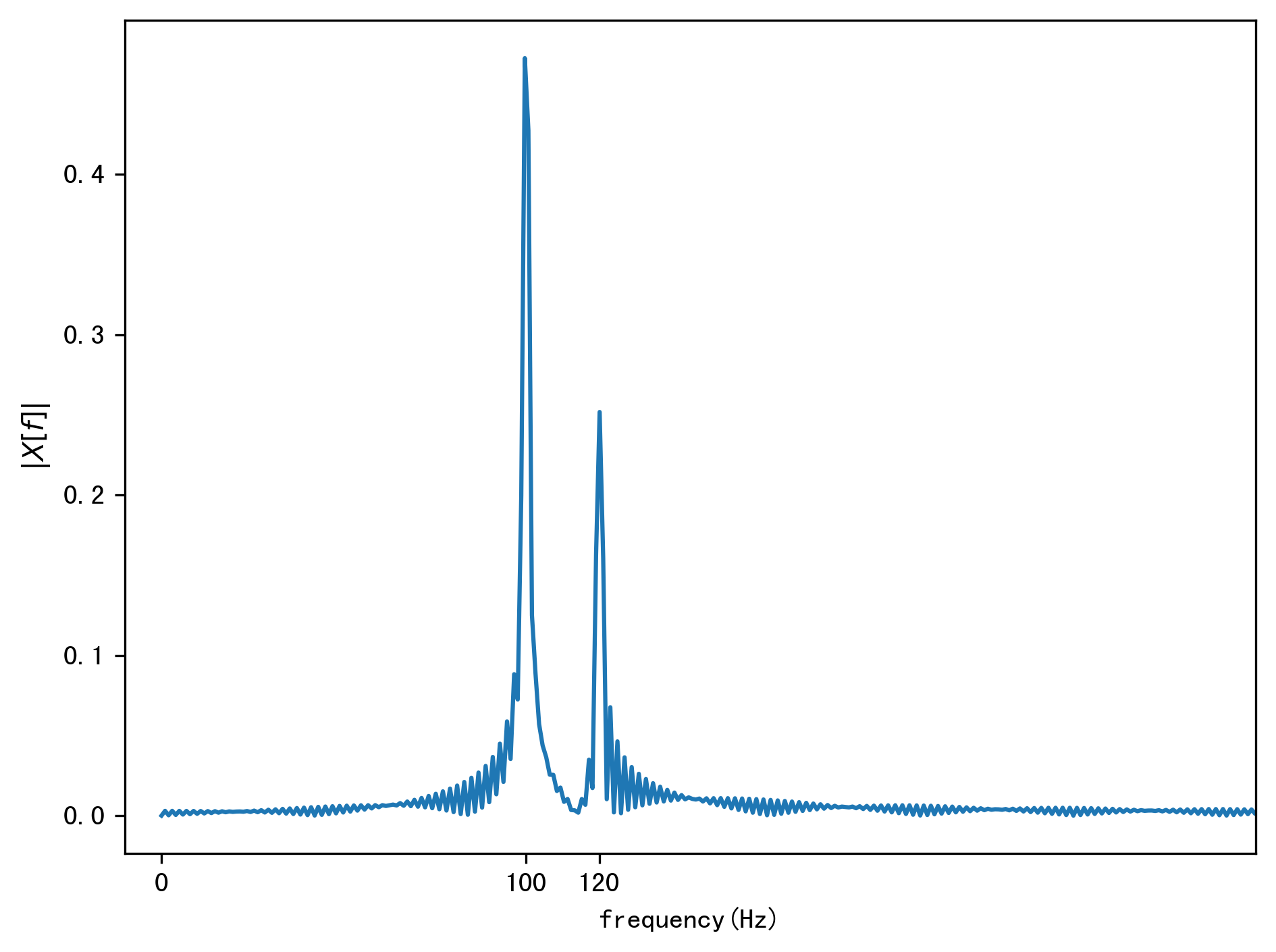
如果按照之前的0.02s的截取长度,那么信号的频率分辨力为:
因此是无法分辨100Hz和120Hz这两个信号,我们可以从下面的频域图中看到,这两个信号的频谱重叠在一起了。
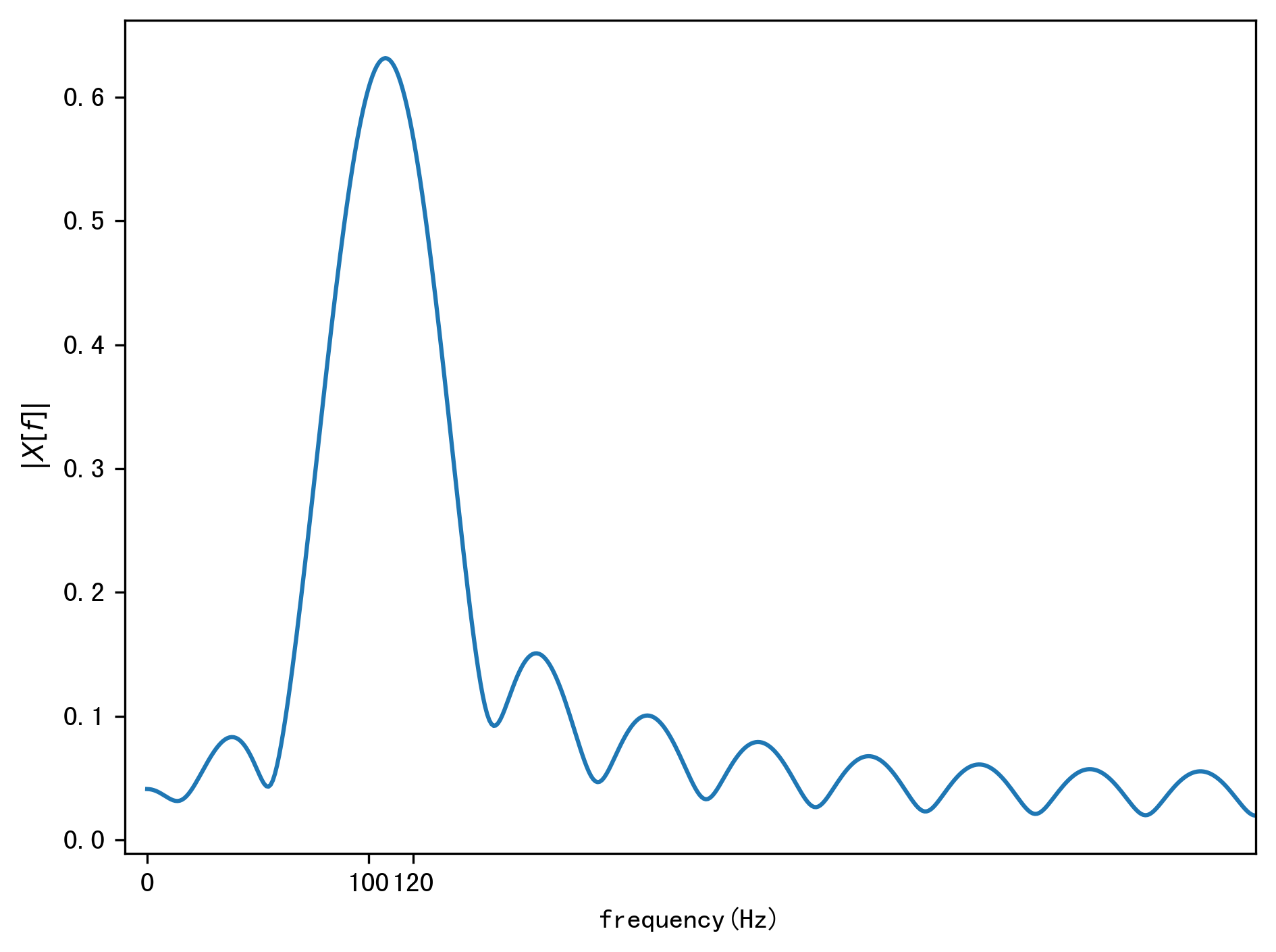
因此如果要分辨这两个信号,我们需要增加信号的截取长度,至少要0.05秒以上才可以分辨这两个信号。
人为地增加频率的抽样点数,是不会增加频率分辨力的。增加频率的抽样点数一方面为了做FFT计算时凑成2的整数倍,另一方面可以让频域图更加平滑,看到更多的离散的频率点的值。