#! https://zhuanlan.zhihu.com/p/657011183

数字信号处理中各种变换之间的联系

下图描述了各种变换之间的联系：

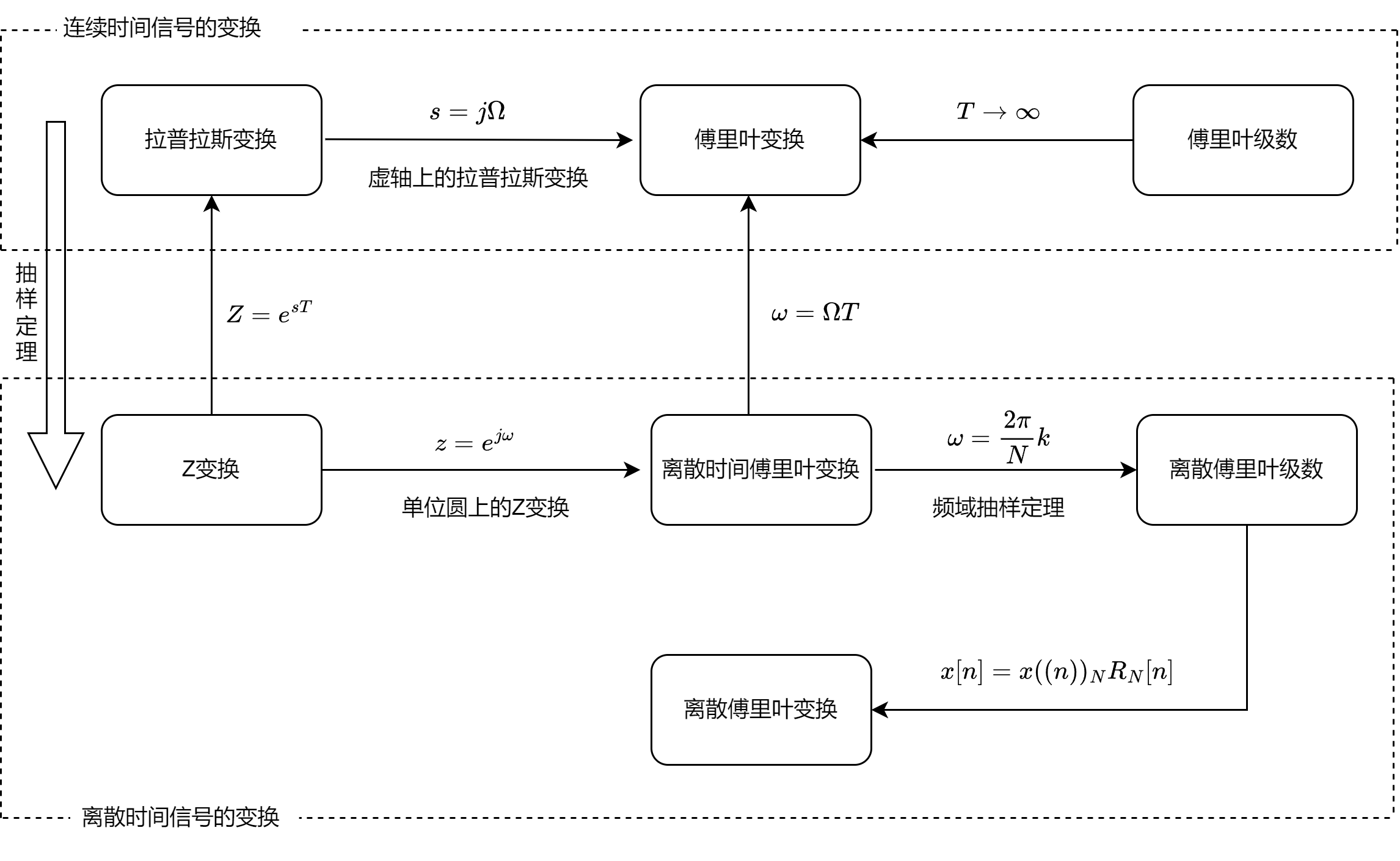
Z变换与DTFT

\(\displaystyle X(z)=\sum _{n=-\infty }^{\infty }x[n]z^{-n}\) 其中复变量\(z=re^{j\omega}\)，\(r\)为半径，\(\omega\)为数字频率。当半径\(r=1\)时，Z变换退化为离散时间傅里叶变换，即： \({\displaystyle X(e^{j\omega})=\sum _{n=-\infty }^{\infty }x[n]e^{-j\omega n}}\) 换句话说DTFT是单位圆上的Z变换。 从时域上分析，离散时间信号的傅里叶变换存在且连续的条件是信号绝对可和，从Z域上分析，其收敛域必须包含单位圆。

Z变换与拉普拉斯变换的联系

Z变换与拉普拉斯变换的联系可以从理想抽样信号的拉普拉斯变换得出。

给定一连续时间信号\(x(t)\)，其理想抽样信号可以表示为：

\(\displaystyle \hat x(t) = \sum_{n=-\infty}^{\infty}x(nT)\delta (t-nT)\)

其拉普拉斯变换如下：

\(\displaystyle \hat X(s) = \int_{-\infty}^{\infty}\sum_{n=-\infty}^{\infty}x(nT)\delta (t-nT)e^{-st}dt = \sum_{n=-\infty}^{\infty}x(nT)e^{-sTn}=\sum_{n=-\infty}^{\infty}x(n)e^{-sTn}\)

令\(z=e^{sT}\), 得到

\(\displaystyle X(z)|_{z=e^{sT}}=\hat X(s)= \sum_{n=-\infty}^{\infty}x(n)e^{-sTn}\)

因此，当\(z=e^{sT}\)时，Z变换等效为拉普拉斯变换。

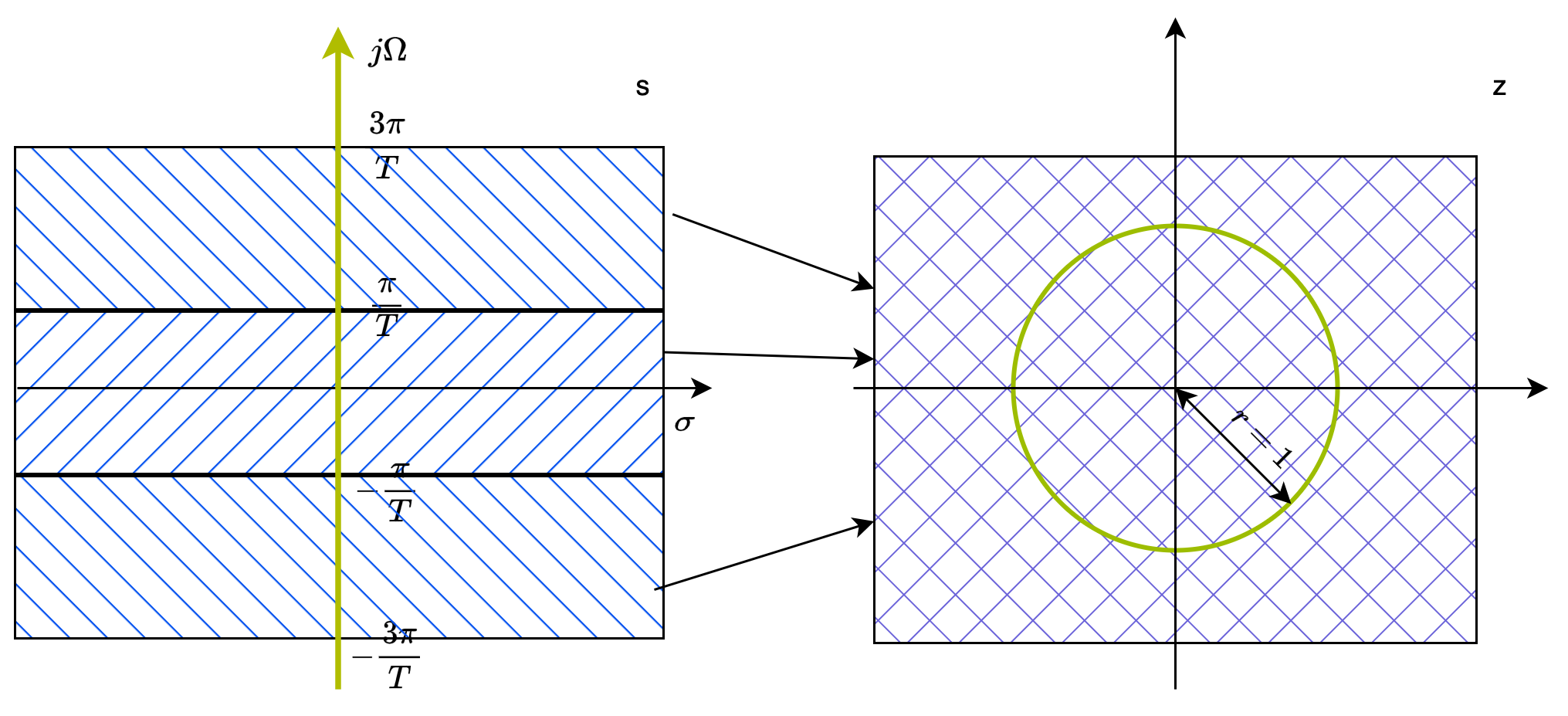
用极坐标表示z，即\(z=re^{j\omega}\)，用直角坐标表示s，即\(s=\sigma+j\Omega\)，于是可以得到：

\(\displaystyle r=e^{\sigma T}\)

\(\displaystyle \omega=\Omega T\)

从第一个等式，我们可以推导出：

• 当\(Re\{s\}=\sigma<0\)时，\(r=e^{\sigma T}<1\)，因此s域左半平面的收敛域对应z域单位圆内的收敛域。

• 当\(Re\{s\}=\sigma>0\)时，\(r=e^{\sigma T}>1\)，因此s域右半平面的收敛域对应z域单位圆外的收敛域。

• 当\(Re\{s\}=\sigma=0\)时，\(r=e^{\sigma T}=1\)，因此s域虚轴对应z域单位圆。

以上的关系用图形表示如下：

分析第二个等式，由于\(\omega\)是以\(2\pi\)为周期的，\(\Omega\)从\(-\frac{\pi}{T}\)到\(\frac{\pi}{T}\)的s平面对应着整个z平面，同样地，对于\(\Omega\)从\(-\frac{3\pi}{T}\)到\(-\frac{\pi}{T}\)的s平面也对应着整个z平面，以此类推，我们可以得到：s平面与z平面是多对一的关系。可以用下图来表示：

傅里叶变换与DTFT的关系

离散时间傅里叶变换可以看作单位圆的Z变换，因此：\(z = e^{j\omega}\)；傅里叶变换可以看作虚轴的拉普拉斯变换，因此：\(s = j\Omega\)。由上述Z变换与拉普拉斯变换的关系，可以得到傅里叶变换与DTFT的关系如下：

\(\displaystyle X(e^{j\omega})|_{\omega=\Omega T}=\sum_{n=-\infty}^{\infty}x(n)e^{-jn\Omega T}=\hat X(j\Omega)\)

根据抽样定理，抽样信号的频谱可表示为： \(\displaystyle \hat X(j\Omega)=\sum_{n=-\infty}^{\infty}\frac{1}{T}X(j\Omega-jn\Omega_s)\)

综合上面两个表达式可以得到：

\(\displaystyle X(e^{j\omega})|_{\omega=\Omega T}=\sum_{n=-\infty}^{\infty}\frac{1}{T}X(j\frac{\omega}{T}-jn\frac{2\pi }{T})\)

DTFT与DFT的关系

DTFT表示如下： \(\displaystyle X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}\)

其中\(\omega\)是周期为\(2\pi\)的数字频率，我们对频率信号进行抽样，其中抽样间隔为\(2\pi/N\)，这样在一个周期内，我们可以得到\(N\)个采样点，频率上的抽样会造成信号在时域上周期延拓，因此：

\(\displaystyle X(e^{j\omega})|_{\omega = \frac{2\pi}{N}k} = \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}nk}=X[k]\)

也就是说\(X[k]\)的值就是\(X(e^{j\omega})\)在\(\omega = \frac{2\pi}{N}k\)处的值，这样我们就可以用\(X[k]\)来表示\(X(e^{j\omega})\)。

图形化表示

下图描述了信号从连续时间到离散时间各种变换的过程：

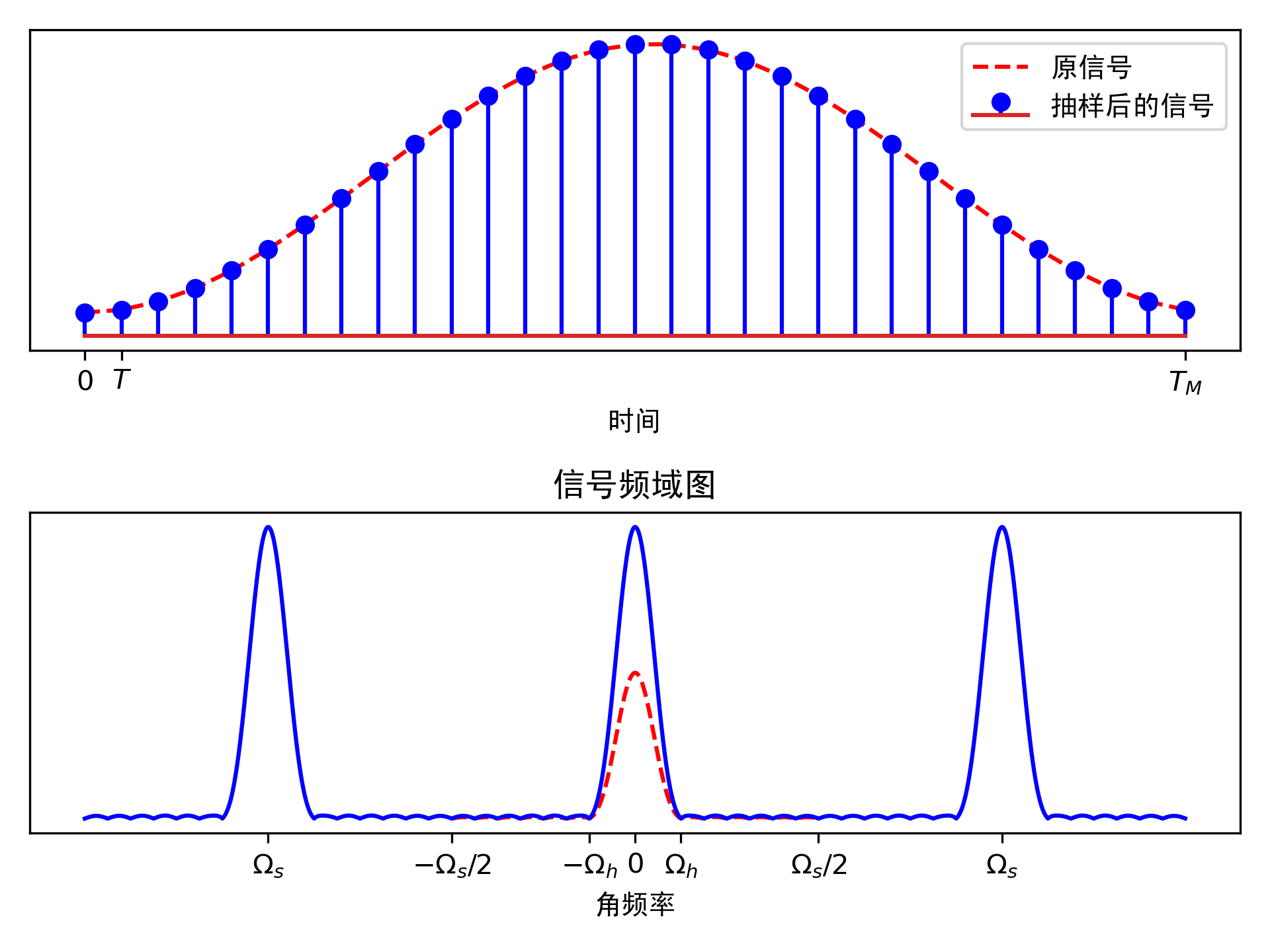
• 连续时间信号经过时域上的抽样（抽样间隔为\(T\))变成离散时间信号，在频域上会造成信号的周期延拓，周期延拓的周期为\(\Omega_s=2\pi/T\)(如果用频率表示就是抽样频率\(f_s=1/T\))，同时会造成频域信号幅值的缩放，缩放大小为\(1/T\)。上面第二幅图的红色虚线表示的是原连续时间信号的频谱，\(\Omega_s/2\)表示的是折叠频率。因此时域上的抽样，必须满足抽样频率大于信号的最高频率的两倍，即信号的最高频率必须小于折叠频率，否则会造成信号在频域上的混叠。

• 用离散时间傅里叶变换表示的信号的频谱跟抽样信号的频谱形状上是一样的，只是横坐标的变量不一样，即: $\(\displaystyle \begin{equation*} X(e^{j\omega})|_{\omega=\Omega T}=\sum_{n=-\infty}^{\infty}\frac{1}{T}X(j\Omega-jn\Omega_s)=\sum_{n=-\infty}^{\infty}\frac{1}{T}X(j\frac{\omega}{T}-jn\frac{2\pi }{T}) \end{equation*}\)$

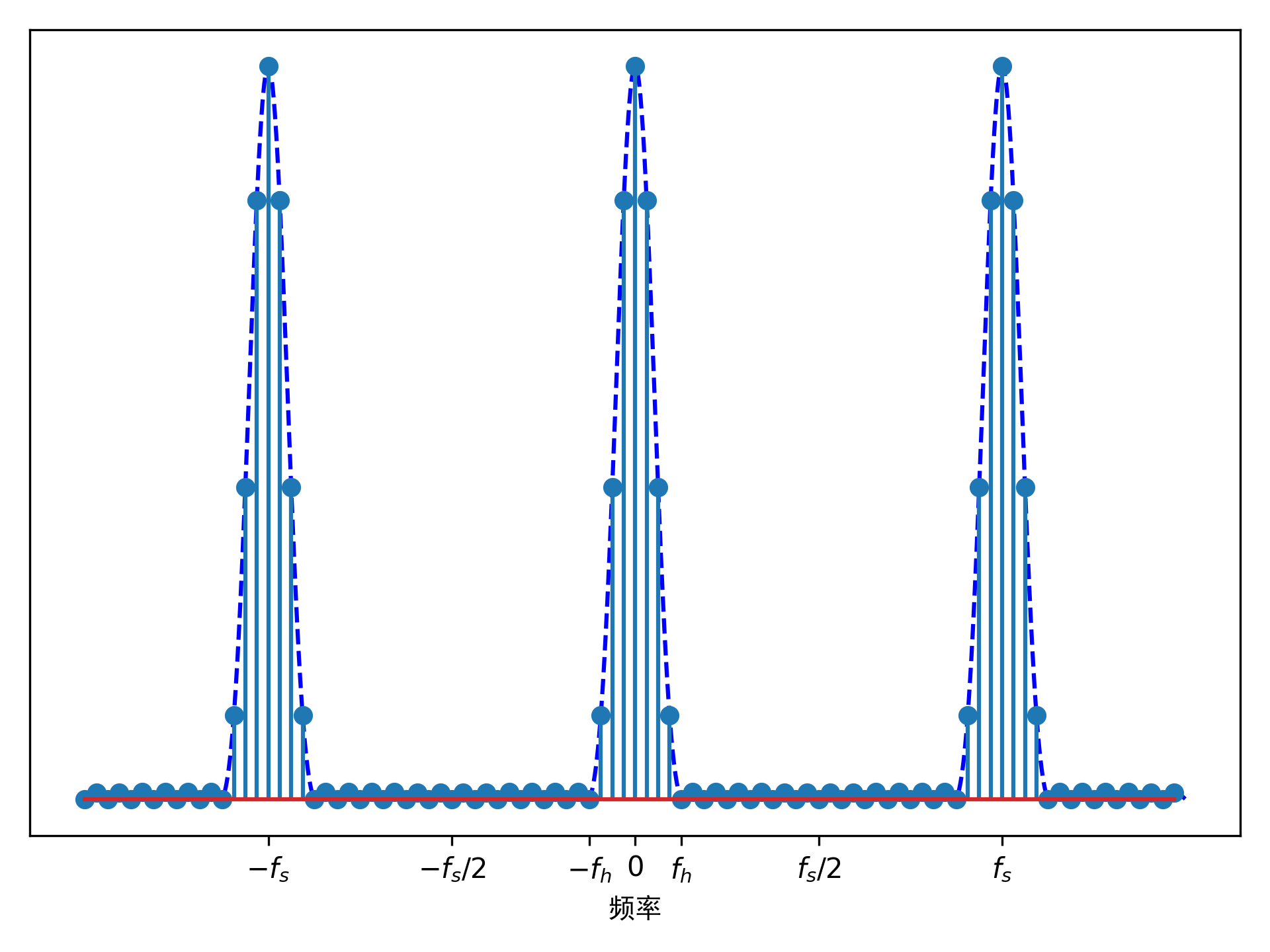
• 频域上的抽样，会造成时域上信号的周期延拓，但没有任何幅值的变化。周期延拓的周期\(T_0\)为频域抽样间隔（这里定义为\(F_0\))的倒数，即周期延拓的周期必须大于原始信号的长度\(T_M\)（即\(T_0 > T_M\))，否则会造成信号在时域上的混叠。

• 信号在时域上抽样，抽样点数\(M=T_M/T\)，信号在频率上的抽样点数\(N=F_s/F_0\)，只有当\(N \geq M\)时，才能保证信号在时域上周期延拓时不混叠，如果\(M<N\)，在做DFT变换时，时域上补上\(N-M\)个零点。

用\(X[k]\)表示\(X(z)\)和\(X(e^{j\omega})\)

既然\(N\)个频域抽样值\(X[k]\)能不失真地代表\(N\)点有限长序列，那么这\(N\)个抽样值\(X[k]\)也一定能够完全地表达整个\(X(z)\)及频率响应\(X(e^{j\omega})\)。

用\(X[k]\)表示\(X(z)\)

有限长序列\(x[n]\)的Z变换定义为：

\(\displaystyle X(z) = \sum_{n=0}^{N-1}x[n]z^{-n}\)

由于

\(\displaystyle x[n] = \frac{1}{N}\sum_{k=0}^{N-1}X[k]W_N^{-nk}\)

因此

\[\begin{split}\begin{split} X(z) & = \sum_{n=0}^{N-1}\frac{1}{N}\sum_{k=0}^{N-1}X[k]W_N^{-nk}z^{-n} \\ & = \frac{1}{N}\sum_{k=0}^{N-1}X[k]\sum_{n=0}^{N-1}W_N^{-nk}z^{-n} \\ & = \frac{1}{N}\sum_{k=0}^{N-1}X[k]\frac{1-W_N^{-KN}Z^{-N}}{1-W_N^{-k}z^{-1}} \\ & =\sum_{k=0}^{N-1}X[k]\frac{1-Z^{-N}}{N(1-W_N^{-k}z^{-1})}\end{split}\end{split}\]

令

\(\displaystyle \phi_k(z) = \frac{1}{N}\frac{1-Z^{-N}}{1-W_N^{-k}z^{-1}}\)为插值函数

则

\(\displaystyle X(z) = \sum_{k=0}^{N-1}X[k]\phi_k(z)\)

分析插值函数的零极点可知，其零点如下

\(\displaystyle z = e^{j\frac{2\pi r}{N}} \quad r=0, \ldots, N-1\)

其有一个极点在\(z=e^{j\frac{2\pi k}{N}}\)处，在0点有\(N-1\)阶极点。插值函数的一阶极点可以跟零点抵消，因此插值函数只在本身抽样点处不为零，在其他的\(N-1\)抽样点处都为零。

用\(X[k]\)表示\(X(e^{j\omega})\)

将\(z=e^{j\omega}\)代入上部分推导的\(X(z)\)，得到：

\(\displaystyle X(e^{j\omega}) = \sum_{k=0}^{N-1}X[k]\phi_k(e^{j\omega})\)

其中插值函数\(\phi_k(e^{j\omega})\)的表达式为：

\[\begin{split}\begin{split}\phi_k(e^{j\omega})& = \frac{1}{N}\frac{1-e^{-jN\omega}}{1-e^{-j(\omega-\frac{2k\pi}{N})}} \\ & = \frac{1}{N}\frac{\sin(\omega N/2)}{\sin((\omega-2k\pi/N)/2)}e^{-j(\frac{N-1}{2}\omega)+\frac{k\pi}{N}} \\ & =\frac{1}{N}\frac{\sin(N(\omega/2-\pi k/N))}{\sin(\omega/2-k\pi/N)}e^{j\frac{k\pi}{N}(N-1)}e^{-j(\frac{N-1}{2}\omega)} \end{split}\end{split}\]

令

\(\displaystyle \phi_k(\omega) = \phi(\omega-2\pi k/N)\)

则

\(\displaystyle \phi(\omega) = \frac{1}{N}\frac{\sin(N\omega/2)}{\sin(\omega/2)}e^{-j(\frac{N-1}{2}\omega)}\)

因此

\(\displaystyle X(e^{j\omega}) = \sum_{k=0}^{N-1}X[k]\phi_k(\omega-2\pi k/N)\)

插值函数满足如下关系：

\(\displaystyle \phi(\omega-2\pi k/N)=\begin{cases} 1, & \omega =2\pi k/N =\omega_k\\ 0, & \omega = 2\pi i/N = \omega_i, i \neq k& \end{cases}\)

因此，插值函数只在本身抽样点处不为零，在其他的\(N-1\)抽样点处都为零。

我们可以得到：

\(\displaystyle X(e^{j\omega})|_{\omega = \frac{2\pi}{N}k} =X[k]\)