离散傅里叶级数(DFS)
离散傅里叶级数指的是任何周期序列都可以由谐波相关的复指数序列的加权和组成。
\(\displaystyle \tilde X[k] = \sum_{n = 0}^{N-1} \tilde x[n] \cdot e^{-j\frac{2\pi}{N}kn}\)
\(\tilde x[n]\)是周期为\(N\)的离散时间信号,即\(\tilde x[n] = \tilde x[n + N]\);
跟连续时间周期信号的傅里叶级数中无限项谐波相关复指数函数的加权和不同,这里是有限项的加权和;
\(\tilde X[k]\)是\(\tilde x[n]\)的离散傅里叶级数,其周期同样是\(N\);
时域是离散的、周期的,频域也是离散的,周期的。
定义\(W_N = e^{-j\frac{2\pi}{N}}\),则离散傅里叶级数可以写成:
\(\displaystyle \tilde X[k] = \sum_{n = 0}^{N-1} \tilde x[n] \cdot W_N^{kn}\)
离散傅里叶级数的反变换为:
\(\displaystyle \tilde x[n] = \frac{1}{N} \sum_{k = 0}^{N-1} \tilde X[k] \cdot W_N^{-kn}\)
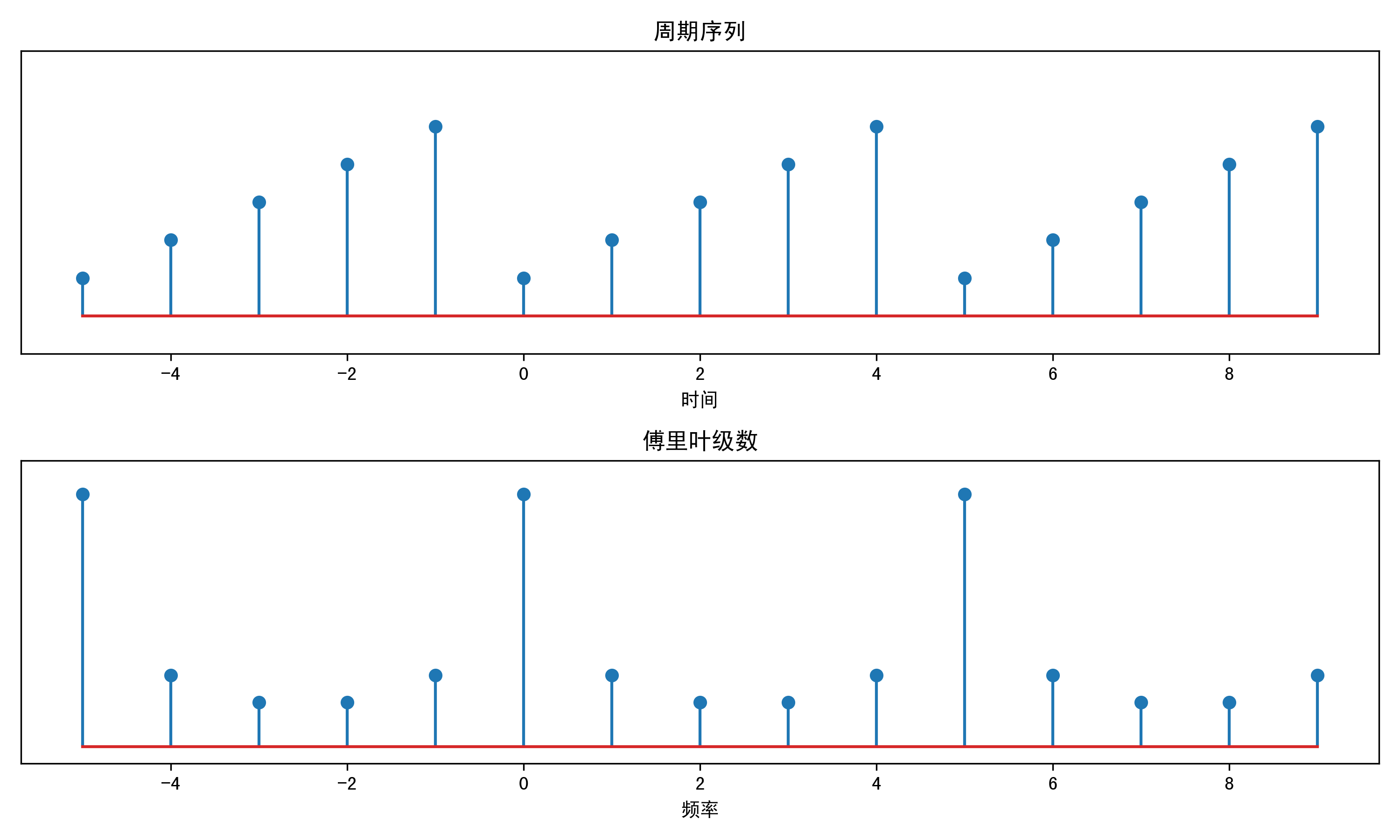
周期序列的时域和其离散傅里叶级数如下图所示:
离散傅里叶级数的性质
\[\begin{split}\begin{array}{|c|c|}
\hline 周期序列 & 离散傅里叶级数 \\
\hline \tilde x[n] & \tilde X[k] \\
\hline \tilde x_1[n] + b\tilde x_2[n] & a\tilde X_1[k] + b\tilde X_2[k] \\
\hline
\tilde x[n - m] & W_N^{km}\tilde X[k] \\
\hline
W_N^{-ln} \tilde x[n] & \tilde X[k-l] \\
\hline
\tilde X[n] & N \tilde x[-k] \\
\hline
\sum_{m=0}^{N-1} \tilde x[m] \tilde x^*[n-m] \quad 圆周卷积 & \tilde X_1[k]\cdot \tilde X_2[k] \\
\hline
\tilde x_1[n]\cdot \tilde x_2[n] & \frac{1}{N}\tilde X_1[k] * \tilde X_2[k] \quad 圆周卷积 \\
\hline
\tilde x^*[n] & \tilde X^*[-k] \\
\hline
\tilde x^*[-n] & \tilde X^*[k] \\
\hline
\textrm{Re}\{\tilde x[n]\} & \tilde X_e[k] = \frac{1}{2}(\tilde X[k] + \tilde X^*[-k]) \\
\hline
j\textrm{Im}\{\tilde x[n]\} & \tilde X_o[k] = \frac{1}{2}(\tilde X[k] - \tilde X^*[-k]) \\
\hline
\tilde x_e[n] = \frac{1}{2}(\tilde x[n] + \tilde x^*[-n]) & \textrm{Re}\{\tilde X[k]\} \\
\hline
\tilde x_o[n] = \frac{1}{2}(\tilde x[n] - \tilde x^*[-n]) & j\textrm{Im}\{\tilde X[k]\} \\
\hline
当\tilde x[n]为实序列时 &
\begin{aligned}
\tilde X[k]为共轭对称序列,& 即\tilde X[k] = \tilde X^*[N-k] \\
\textrm{Re}\{\tilde X[k] \}& =\textrm{Re}\{\tilde X^*[-k]\} \\
\textrm{Im}\{\tilde X[k] \}& =-\textrm{Im}\{\tilde X^*[-k] \} \\
|\tilde X[k]| &= |\tilde X[-k]| \\
\angle \tilde X[k] &= -\angle \tilde X[-k]
\end{aligned} \\
\hline
当\tilde x[n]为实偶序列时 & \textrm{Re}\{\tilde X[k]\} \\
\hline
当\tilde x[n]为实奇序列时 & j\textrm{Im}\{\tilde X[k]\}\\
\hline
\end{array} \end{split}\]
离散傅里叶变换(DFT)
离散傅里叶变换是将有限长的离散时间序列转换为离散频率序列的变换。通过取周期序列的一个周期,可以将离散傅里叶级数转换为离散傅里叶变换。
\(\displaystyle \tilde X[k]R_N[k] = \sum_{n = 0}^{N-1} \tilde x[n] W_N^{kn}R_N[k]\)
\(\displaystyle X[k] = \sum_{n = 0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn}, k=0,1,\cdots,N-1\)
\(x[n]\)是周期序列\(\tilde x[n]\)(也可以表示为\(x((n))_N\))的一个周期,即\(x[n] = \tilde x[n]\),\(0 \leq n \leq N-1\);
\(X[k]\)是频域上周期序列\(\tilde X[k]\)(也可以表示为\(X((k))_N\))的一个周期,即\(X[k] = \tilde X[k]\),\(0 \leq k \leq N-1\);
有限长序列在做离散傅里叶变换时,隐含了“周期性”,也就是说我们需要将有限长序列看成是周期序列的一个周期。离散傅里叶变换的各种性质也是由离散傅里叶级数的性质推导出来的。
有限长序列的时域和其离散傅里叶变换如下图所示:
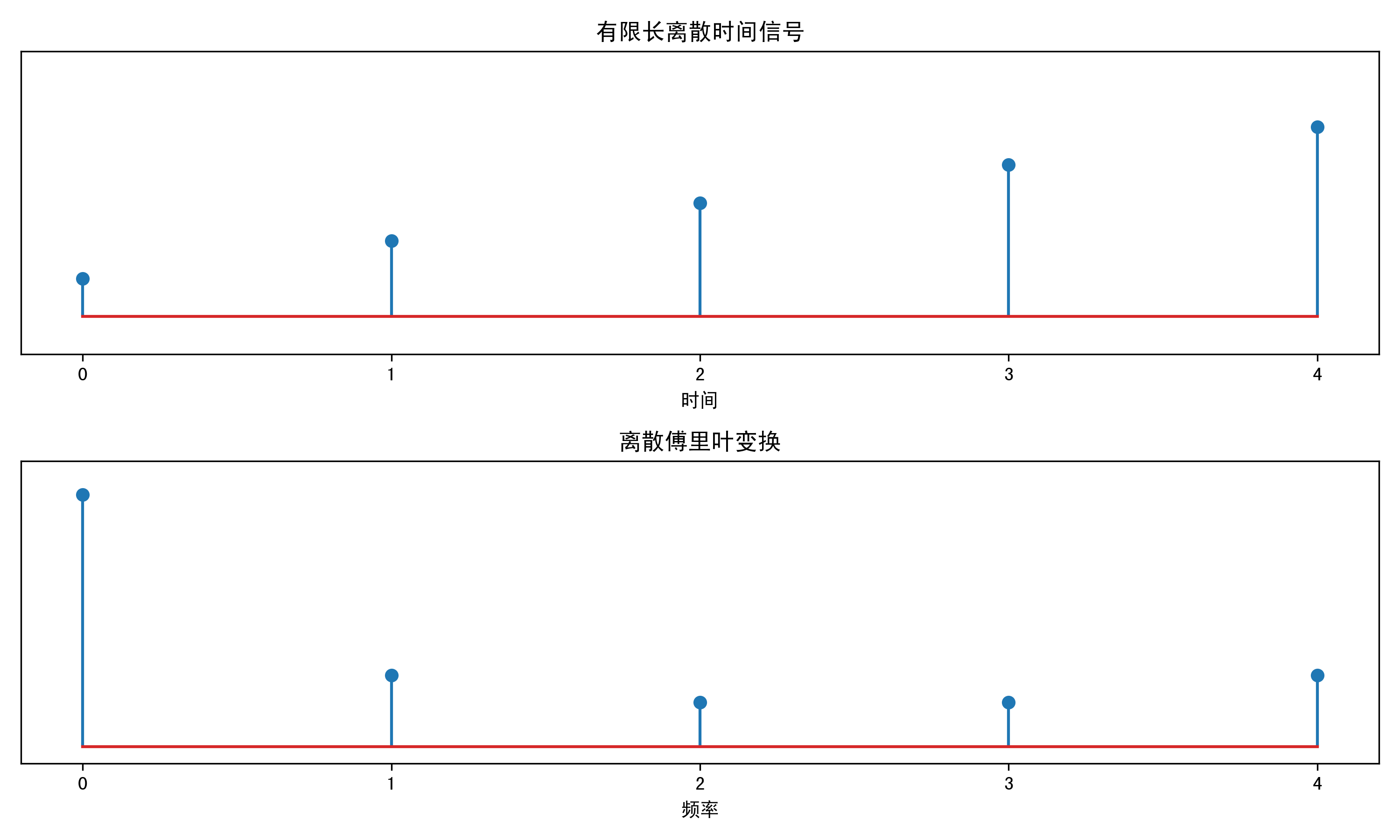
从离散傅里叶级数和离散傅里叶变换的图中可以看出,有限长离散时间信号的傅里叶变换的时域是周期序列取了其中的第一个周期,我们也称之为主值区间,其频域也是周期序列的频域取了其主值区间。
离散傅里叶变换的性质
\[\begin{split}\begin{array}{|c|c|}
\hline 有限长序列,长度为N & N点的离散傅里叶变换 \\
\hline x[n] & X[k] \\
\hline x_1[n] + bx_2[n] & aX_1[k] + b X_2[k] \\
\hline
x((n - m))_N R_N(n) & W_N^{km} X[k] \\
\hline
W_N^{-ln} x[n] & X((k-l))_N R_N(k) \\
\hline
X[n] & N x[N-k] \\
\hline
\sum_{m=0}^{N-1} x[m] x((n-m))_N R_N[n] & X_1[k]\cdot X_2[k] \\
\hline
x_1[n]\cdot x_2[n] & \frac{1}{N}\sum_{l=0}^N X_1[l] X_2((k-l))_N R_N[k] \\
\hline
x^*[n] & X^*[N-k] \\
\hline
x^*((-n))_N R_N[n] & X^*[k] \\
\hline
\textrm{Re}\{x[n]\} & X_e[k] = \frac{1}{2}(X[k] + X^*((-k))_N)R_N[k]\\
\hline
j\textrm{Im}\{x[n]\} & X_o[k] = \frac{1}{2}(X[k] - X^*((-k))_N)R_N[k] \\
\hline
x_e[n] = \frac{1}{2}(x[n] + x^*((-n))_N)R_N[n] & \textrm{Re}\{X[k]\} \\
\hline
x_o[n] = \frac{1}{2}(x[n] - x^*((-n))_N)R_N[n] & j\textrm{Im}\{X[k]\} \\
\hline
当x[n]为实序列时 &
\begin{aligned}
X[k]为共轭对称序列,& 即 X[k] = X^*[N-k] \\
\textrm{Re}\{ X[k] \}& =\textrm{Re}\{ X^*[N-k]\} \\
\textrm{Im}\{ X[k] \}& =-\textrm{Im}\{ X^*[N-k] \} \\
| X[k]| &= | X[N-k]| \\
\angle X[k] &= -\angle X[N-k]
\end{aligned} \\
\hline
当x[n]为实偶序列时 & \textrm{Re}\{X[k]\} \\
\hline
当x[n]为实奇序列时 & j\textrm{Im}\{X[k]\}\\
\hline
\end{array} \end{split}\]
特殊的应用
在做DFT的时候,通常时域上的输入是实数序列,也就是说\(x[n]\)是实数序列,其频域输出\(|X[k]| = |X[N-k]|, \angle X[k] = -\angle X[N-k]\)。因此,我们只需要计算\(0 \leq k \leq N/2\)的数据,这些数据包括了\(0 \leq k \leq N/2\)的数据和\(N/2+1 \leq k \leq N-1\)的数据。这样做的好处是减少了一半的计算量,同时也减少了一半的存储空间。
利用共轭对称性,可以用一次DFT运算来计算两个实数序列的DFT,因而可以减少计算量。
设\(x_1[n]\)和\(x_2[n]\)为N点的实数序列,其DFT分别为\(X_1[k]\)和\(X_2[k]\),则:
先用这两个实数序列组成一个复数序列\(x[n] = x_1[n] + jx_2[n]\),求其DFT为\(X[k]\),然后利用共轭对称性,可以得到:
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X_1[k] & = DFT\{Re\{x[n]\}\} \\
& = \frac{1}{2}(X[k] + X^*[N-k])
\end{split}\end{equation*}\end{split}\]
\[\begin{split}\displaystyle \begin{equation*} \begin{split} X_2[k] & = DFT\{Im\{x[n]\}\} \\
& = \frac{1}{2j}(X[k] - X^*[N-k])
\end{split}\end{equation*}\end{split}\]

